The travelling salesman problem презентация
Содержание
- 2. The origins of the travelling salesman problem are unclear The travelling
- 3. It was first considered mathematically in the 1930s by Merrill Flood
- 4. History In the 1950s and 1960s, the problem became increasingly popular
- 5. As a graph problem TSP can be modelled as an
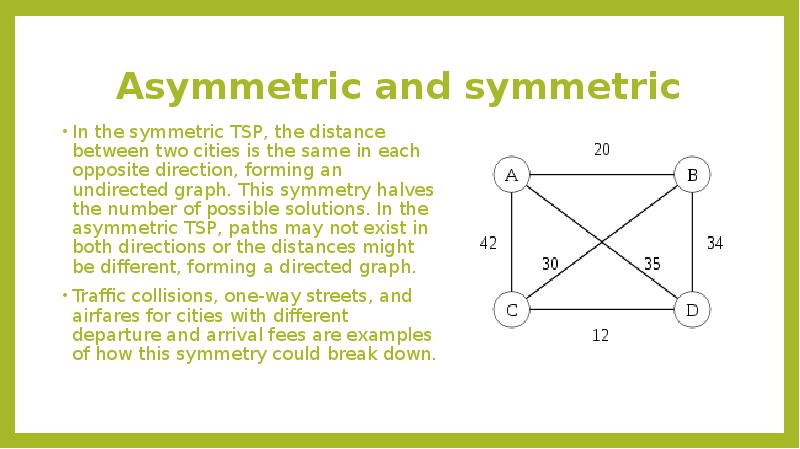
- 6. Asymmetric and symmetric In the symmetric TSP, the distance between two
- 7. Related problems An equivalent formulation in terms of graph theory is:
- 8. Integer linear programming formulation TSP can be formulated as an integer
- 9. Computing a solution The traditional lines of attack for the NP-hard
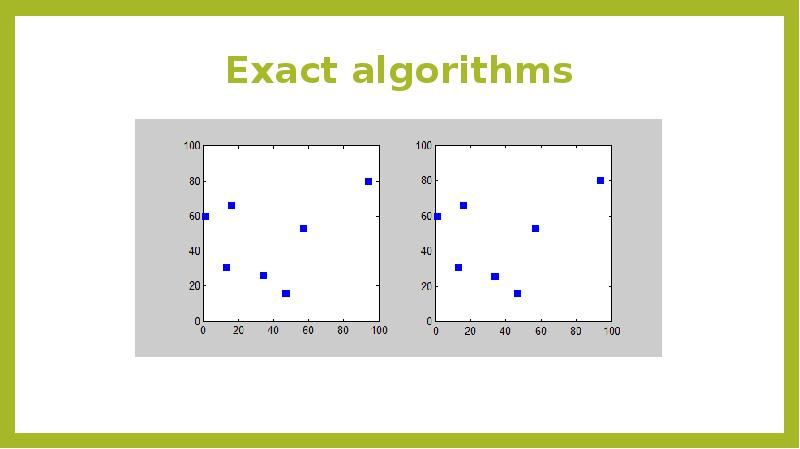
- 10. Exact algorithms The most direct solution would be to try all
- 11. Exact algorithms
- 12. Heuristic and approximation algorithms Various heuristics and approximation algorithms, which quickly
- 13. Constructive heuristics The nearest neighbor (NN) algorithm (or so-called greedy algorithm)
- 14. Christofides' algorithm for the TSP The Christofides algorithm follows a similar
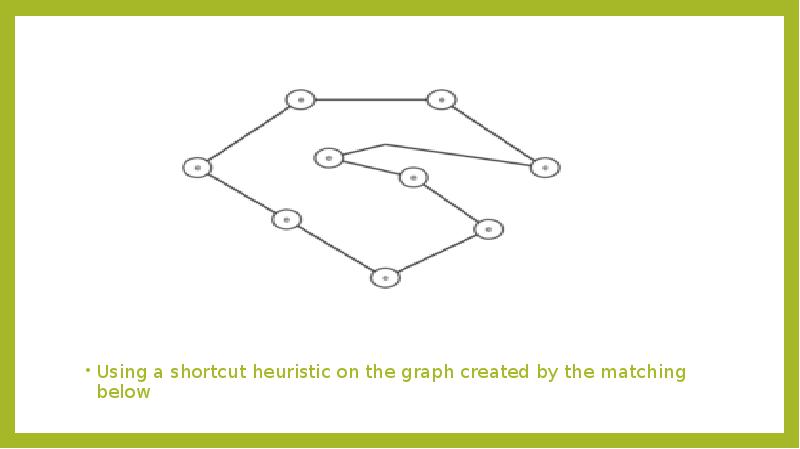
- 15. Using a shortcut heuristic on the graph created by the matching
- 16. Iterative improvement Pairwise exchange The pairwise exchange or 2-opt technique involves
- 17. Randomised improvement Optimized Markov chain algorithms which use local searching heuristic
- 18. Ant colony optimization Artificial intelligence researcher Marco Dorigo described in 1993
- 19. Special cases of the TSP Metric TSP
- 20. Asymmetric TSP
- 21. Analyst's travelling salesman problem There is an analogous problem in
- 22. Computational complexity The problem has been shown to be NP-hard
- 23. Complexity of approximation In the general case, finding a shortest
- 25. Скачать презентацию





















Слайды и текст этой презентации
Похожие презентации