Аналіз зв’язку між змінними: кореляція і регресія презентация
Содержание
- 2. 1. Поняття регресійного аналізу. Функціональний зв’язок – вид зв’язку, коли
- 3. Кореляційний аналіз Кореляційний аналіз – це сукупність статистичних прийомів,
- 4. Коефіцієнт кореляції Пірсона Коефіцієнт кореляції (вибірковий r, генеральний ρ) – показник,
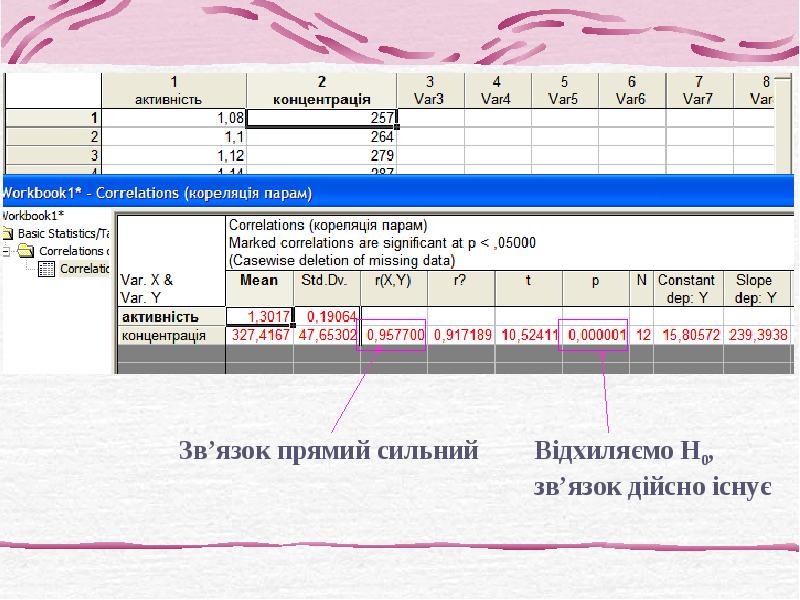
- 5. Напрямок і сила зв’язку: |r|>0.75 – сильний 0.5<|r|<0.75 - середній |r|<0.5
- 10. Cтатистична похибка коефіцієнта кореляції та довірчий інтервал: Вибірковий коефіцієнт r характеризує
- 11. Коефіцієнт кореляції для малих вибірок: Для вибірок з n<30 вводять поправку:
- 12. Статистична значущість різниці коефіцієнтів кореляції Н0: вибірки взяті з одної генеральної
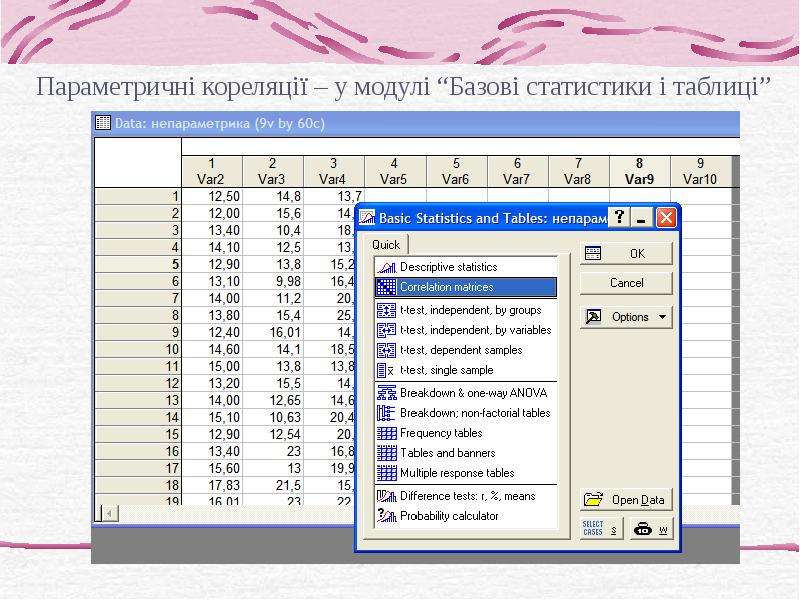
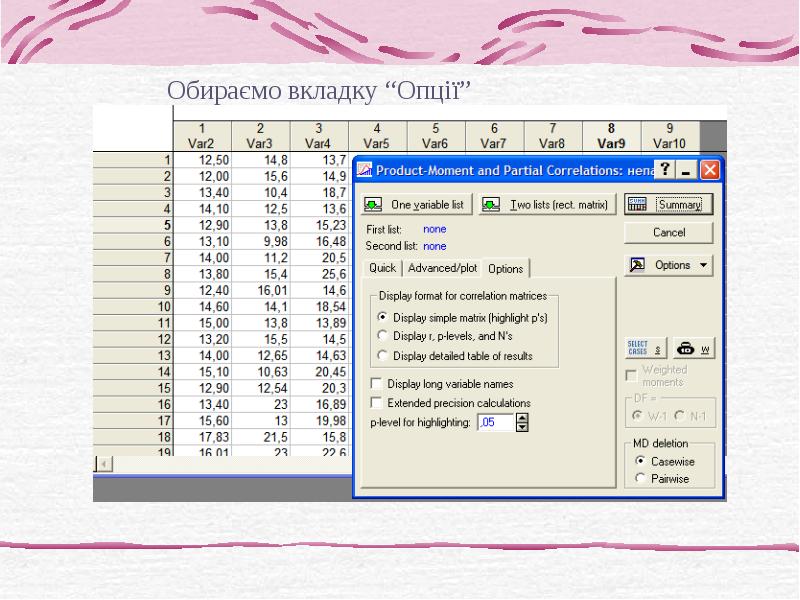
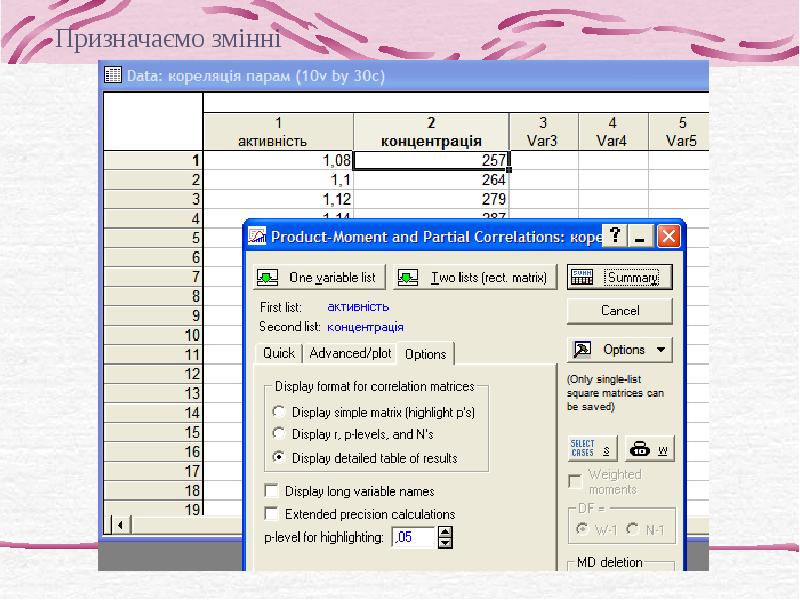
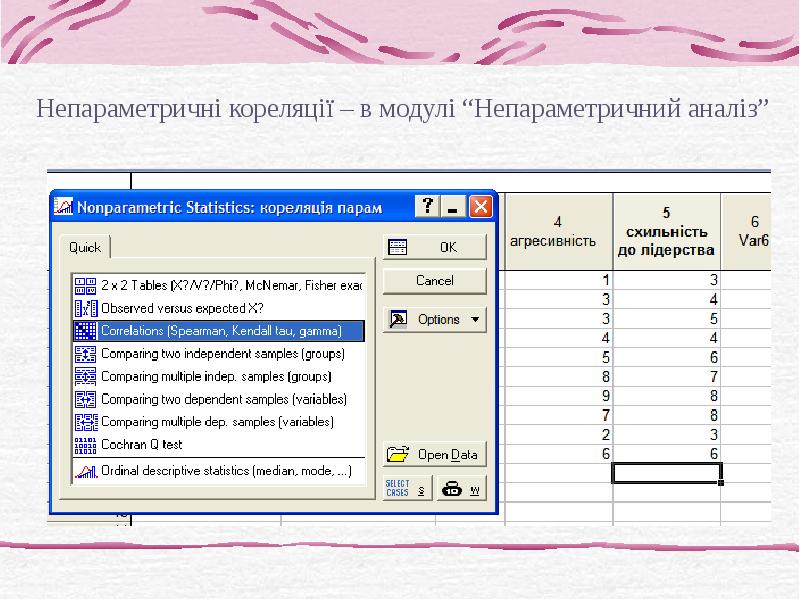
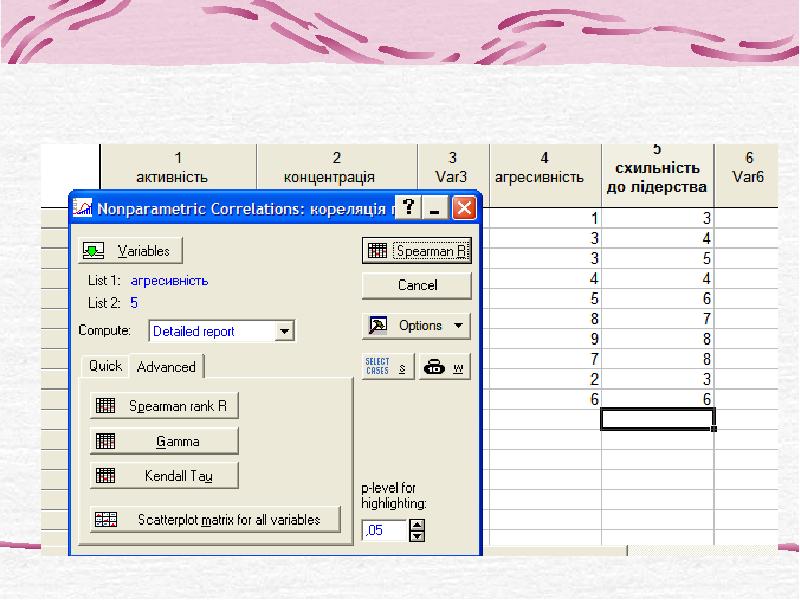
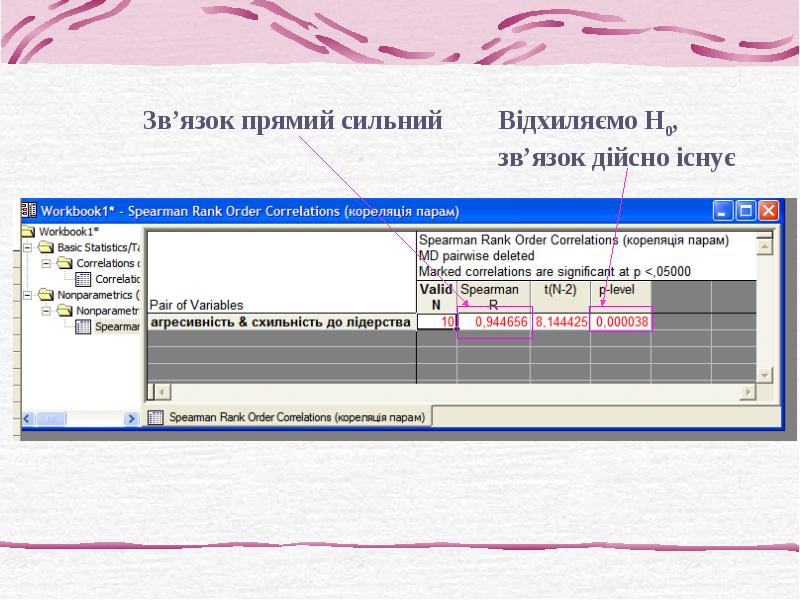
- 13. 2. Непараметричний кореляційний аналіз (коефіцієнти кореляції рангів) Застосовують: без передбачення про
- 17. Cила зв’язку: r2=0.25-0.75 – середній, r2<0.25 – слабкий, r2>0.75
- 18. Зв’язок між якісними ознаками: таблиці 2х2; коефіцієнт асоціації Пірсона rA Маємо
- 19. Бісеріальний коефіцієнт кореляції rBS Використовують, коли одна ознака бінарна (наприклад, стать),
- 20. Регресійний аналіз Регресійний аналіз – це методи статистичного аналізу, які встановлюють
- 22. Лінійна регресія Рівняння зв’язку між х та у має вигляд: Тоді
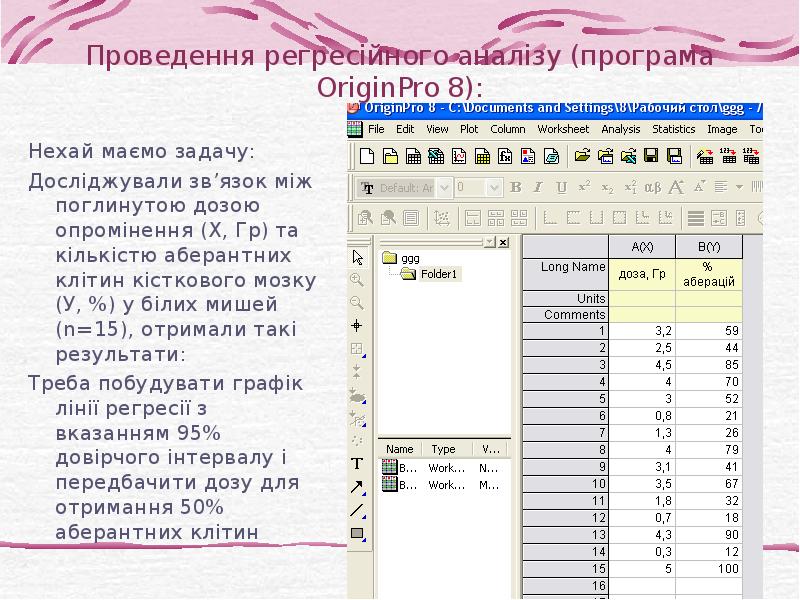
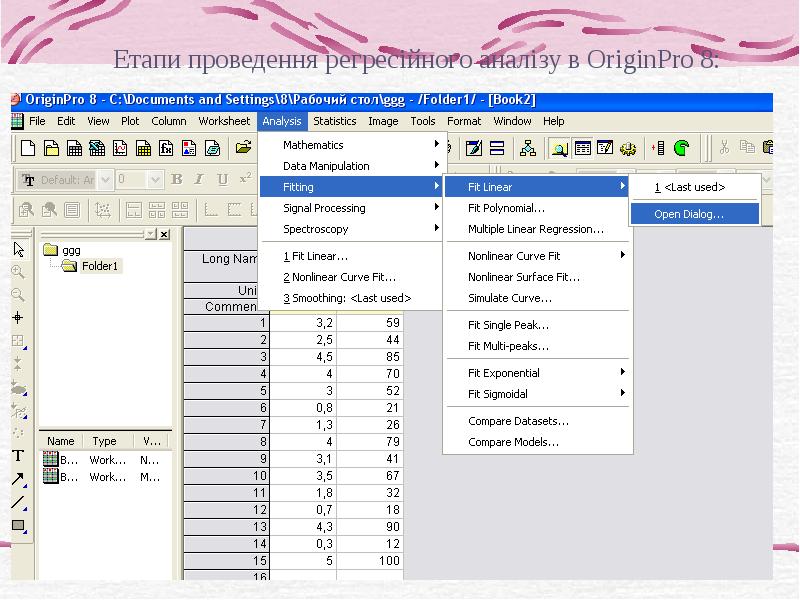
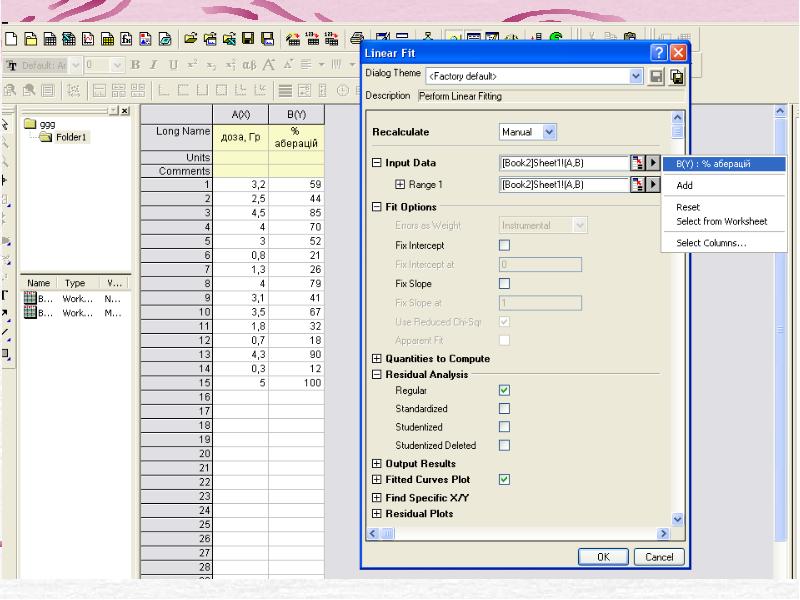
- 23. Проведення регресійного аналізу (програма OriginPro 8): Нехай маємо задачу: Досліджували зв’язок
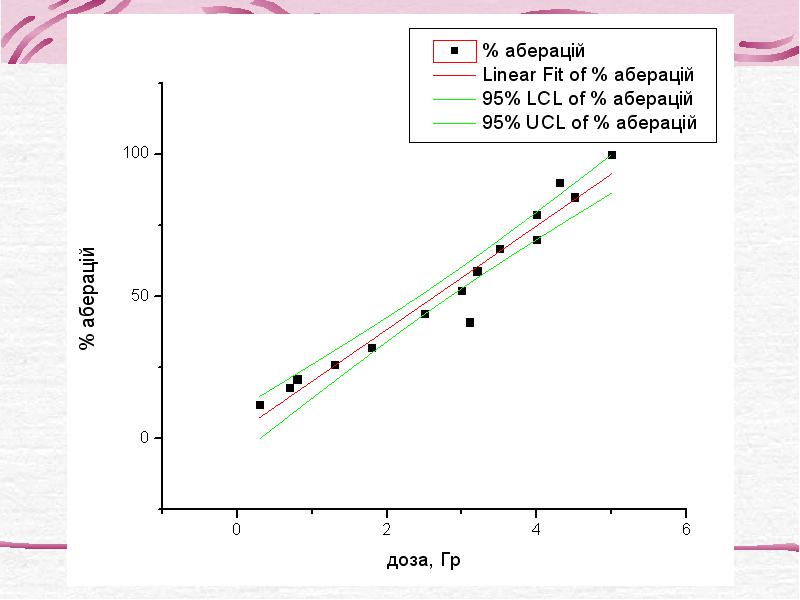
- 27. Довірчий інтервал Для оцінювання похибки при прогнозуванні параметра У по Х
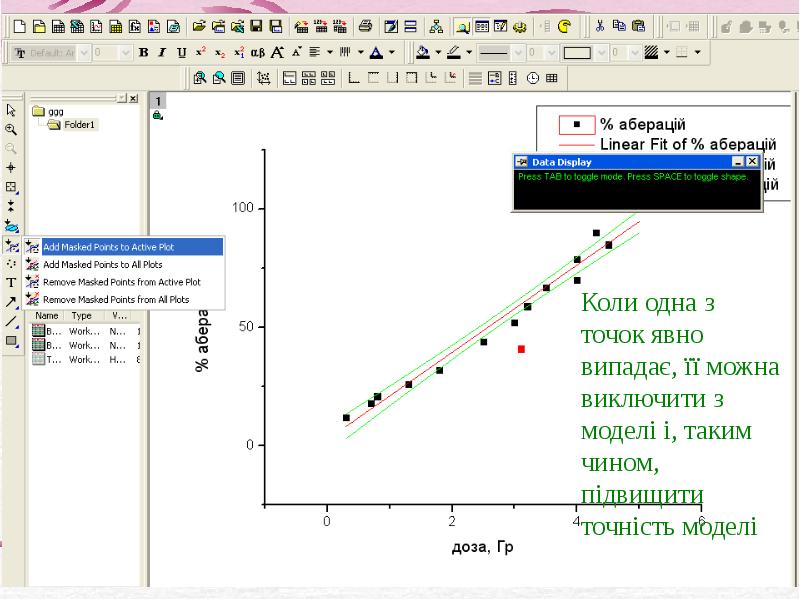
- 30. Для цього ми спочатку з групи інструментів Regional Mask Tool вибираємо
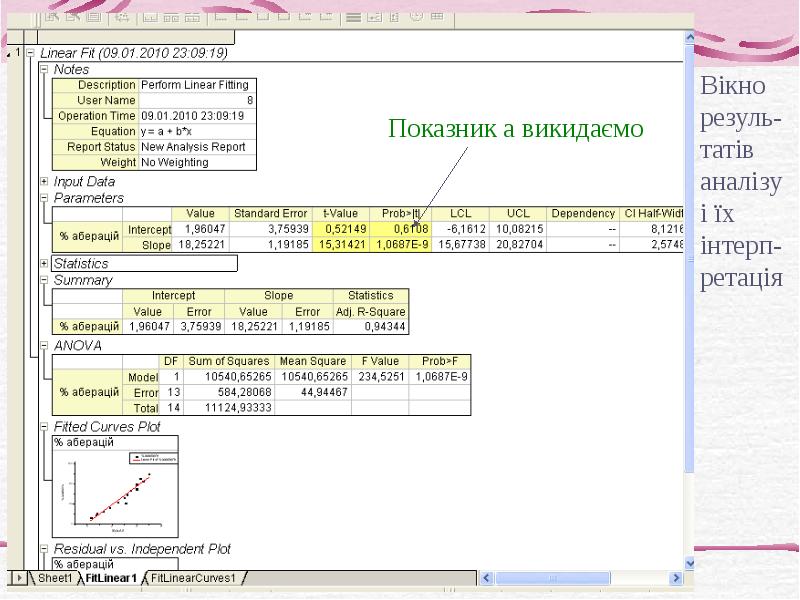
- 31. Дисперсійний аналіз – засіб перевірки значущості моделі: Наслідком дисперсійного аналізу є
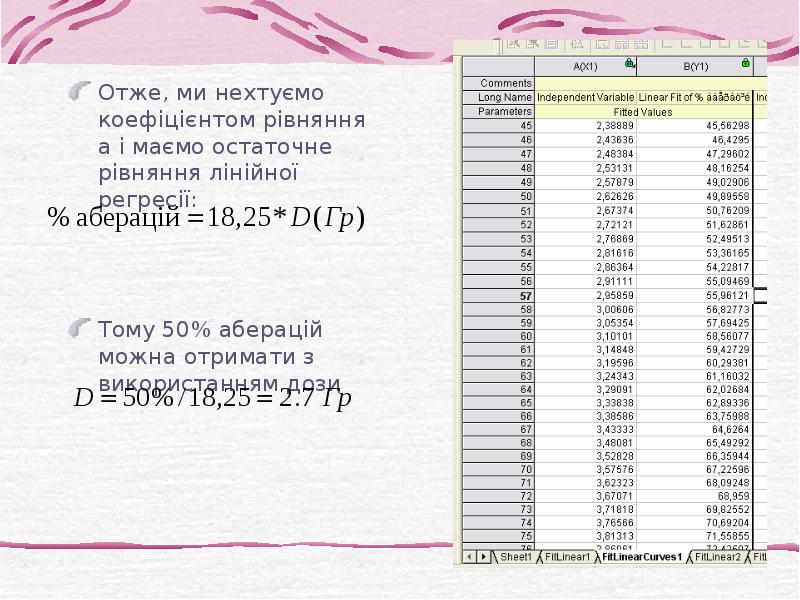
- 32. Отже, ми нехтуємо коефіцієнтом рівняння а і маємо остаточне рівняння лінійної
- 33. Інтерпретація результатів: Коли для моделі р<0,05 – регресійна модель адекватно описує
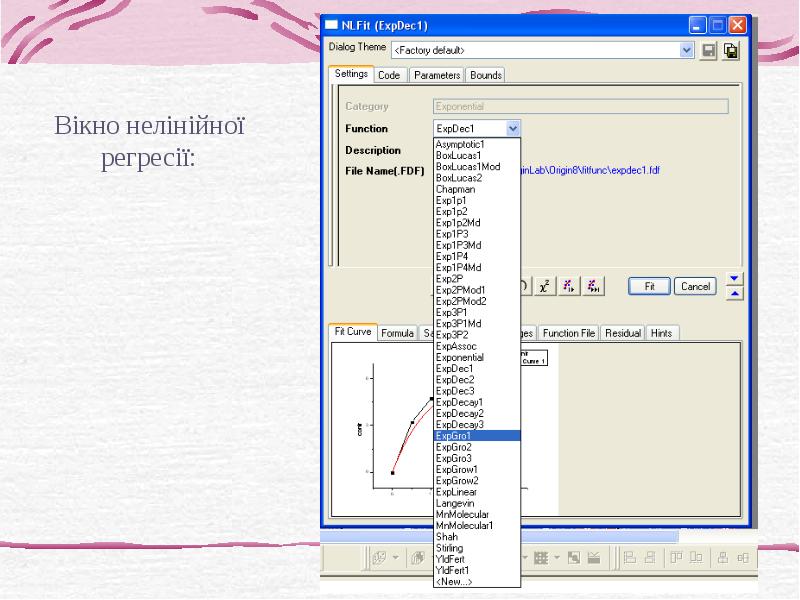
- 34. Нелінійний регресійний аналіз Найбільш часто зустрічаються у біології такі нелінійні залежності:
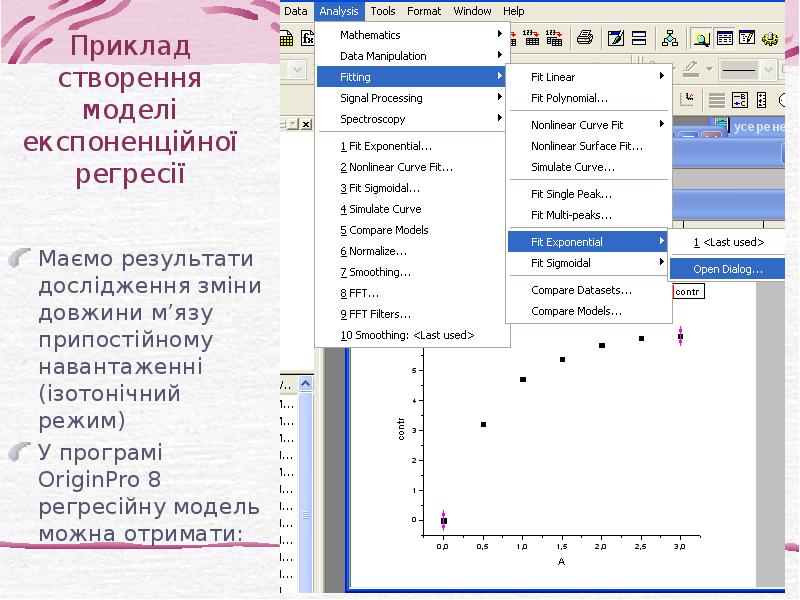
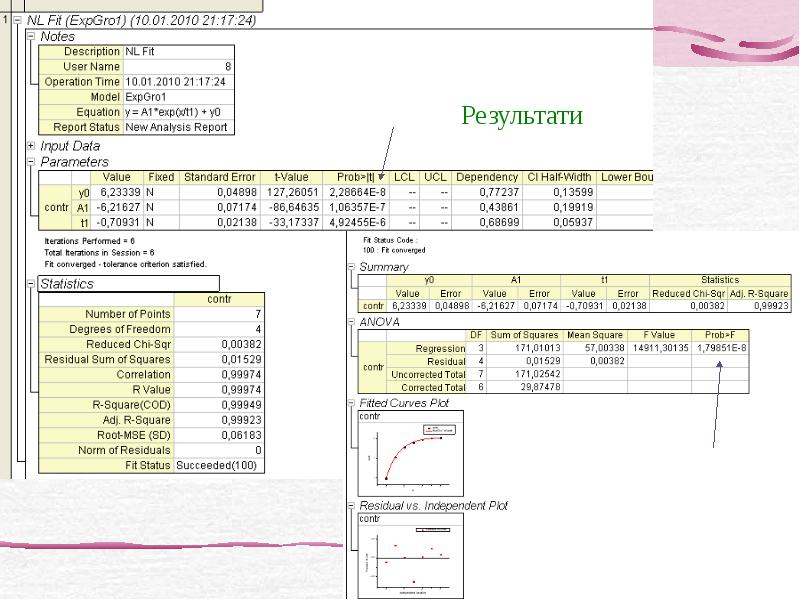
- 35. Приклад створення моделі експоненційної регресії Маємо результати дослідження зміни довжини м’язу
- 38. Скачать презентацию




















Слайды и текст этой презентации
Скачать презентацию на тему Аналіз зв’язку між змінними: кореляція і регресія можно ниже:
Похожие презентации





























