Чистые и смешанные стратегии. Характеризация равновесия по Нэшу презентация

Отображение наилучших откликов ⊐ G = {I ; S ; U}. s = (s1 , s2 , … , sn) ∈ S ; (s1 , s2 , … , sn) → b1(s–1) × b2(s–2) × … × bn(s–n) B: S → S

Характеризация равновесия по Нэшу ⊐ G = {I ; S ; U}, s∗ ∈ S ; B: S → S – отображение наилучших откликов. s∗ – равновесие по Нэшу ⇔ s∗ – неподвижная точка отображения наилучших откликов, т.е. s∗ ∈ B (s∗).

Квазивогнутые функции (quasiconcave) ⊐ F: ℝm → ℝ1. F – квазивогнутая функция, если для ∀ a ∈ ℝ1 {x ∈ ℝm | F(x) ≥ a} – выпуклое.

Теорема (достаточные условия существования равновесия по Нэшу) ⊐ G = {I ; S ; U}; для ∀ i ∈ I ∃mi: Si ⊂ ℝmi. Если для ∀ i ∈ I (1) Si непусто, выпукло и компактно; (2) ui непрерывна; (3) ui(s1 , s2 , … , sn) квазивогнута по si ; то NE(G) ≠ ∅.

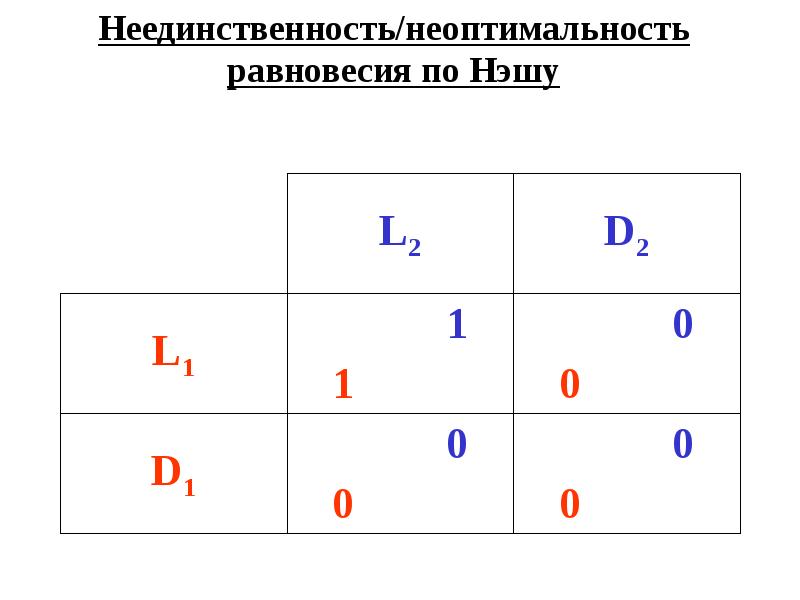
Неединственность/неоптимальность равновесия по Нэшу

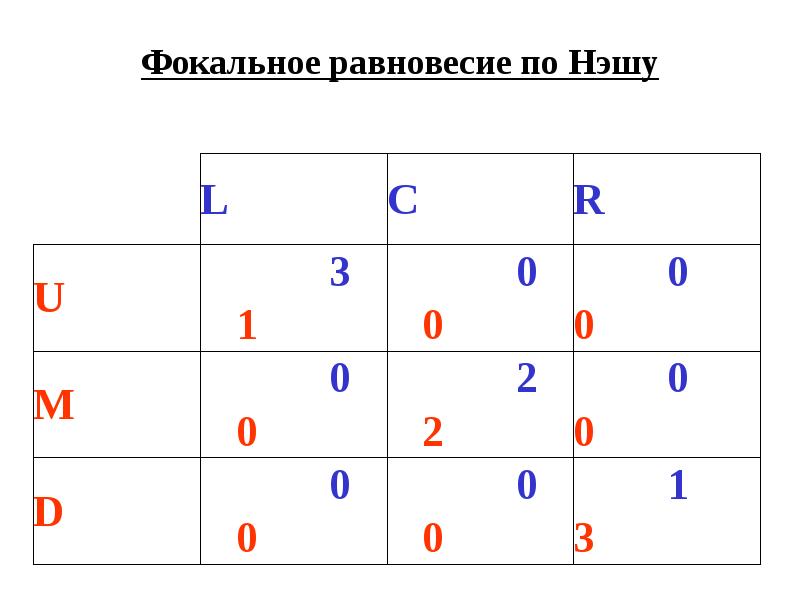
Фокальное равновесие по Нэшу

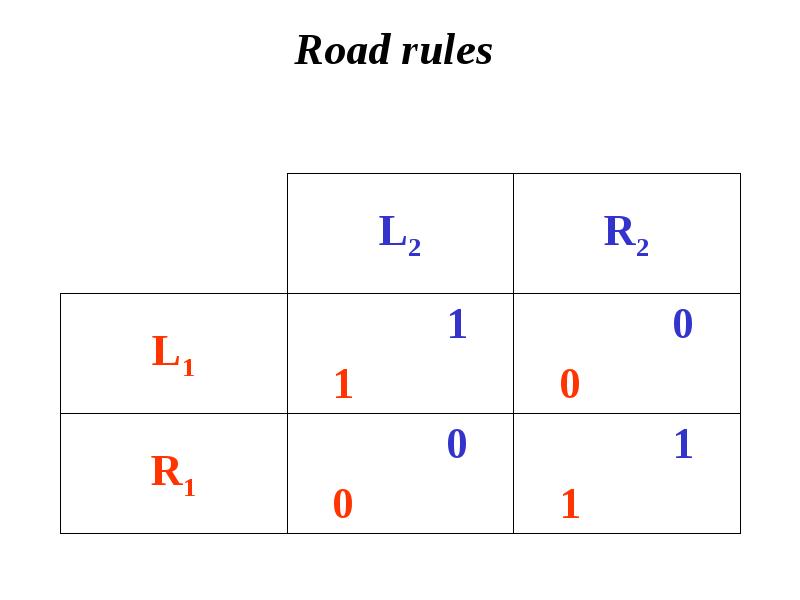
Road rules

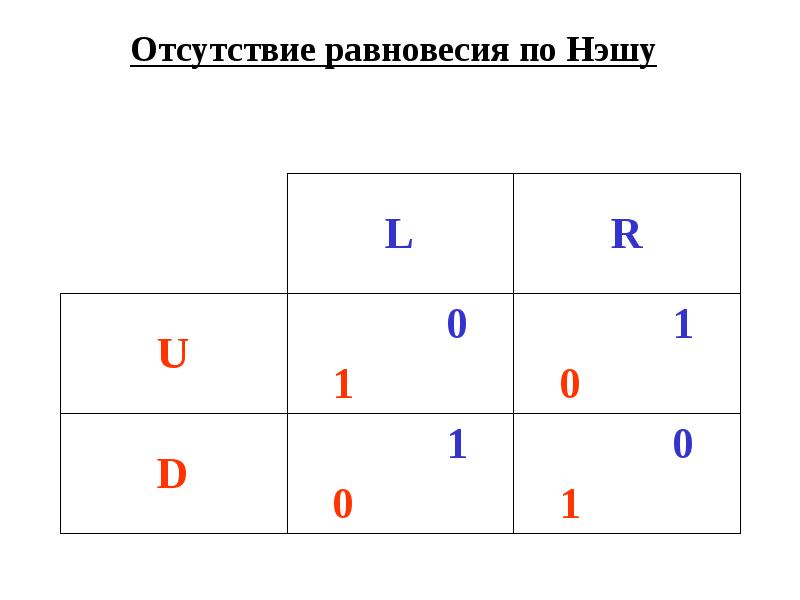
Отсутствие равновесия по Нэшу

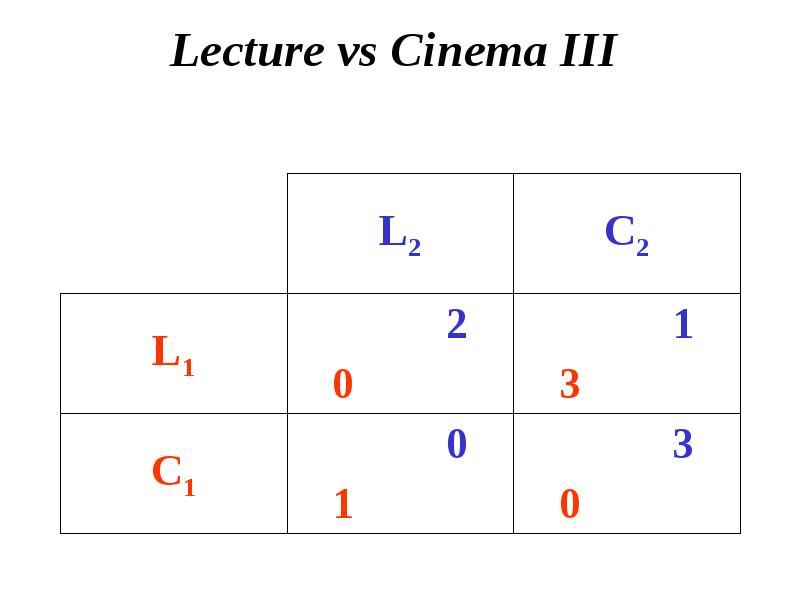
Lecture vs Cinema III

Симплексы ⊐ m ∈ ℕ. Симплекс размерности m – 1 есть S (m – 1) = {x = (x1 , x2 , … , xm) ∈ ℝm | xj ≥ 0 для ∀j = 1, …, m ; x1 + x2 + … + xm = 1}.

Чистые и смешанные стратегии (pure and mixed strategies) ⊐ G = {I ; S ; U}, для ∀ i ∈ I |Si| = mi ∈ ℕ. ⊐ i ∈ I. Смешанная стратегия σi: Si → [0; 1] ставит в соответствие каждой чистой стратегии si ∈ Si вероятность σi(si) ≥ 0 того, что si будет выбрана, причем

Множества и профили смешанных стратегий ⊐ G = {I ; S ; U}, для ∀ i ∈ I |Si| = mi ∈ ℕ. Для ∀ i ∈ I множество его смешанных стратегий Σi есть симплекс размерности mi – 1. Набор σ = (σ1, σ2, …, σn) называется профилем смешанных стратегий. σ ∈ Σ = Σ1 × Σ2 × … ×Σn – пространство смешанных стратегий игры G

Выигрыши по наборам смешанных стратегий ⊐ σ = (σ1, σ2, …, σn) – профиль смешанных стратегий для игры G = {I ; S ; U}, i ∈ I . Выигрыш игрока i, соответствующий профилю σ, есть

Смешанное расширение конечной игры (mixed expansion) ⊐ G = {I ; S ; U} – конечная игра n игроков; Σ = Σ1 × Σ2 × … ×Σn , где Σi – множество смешанных стратегий игрока i ∈ I. Смешанным расширением игры G называется такая игра Γ = {I ; Σ ; U} , что

Носитель смешанной стратегии (mixed strategy support) ⊐ G = {I ; S ; U} – конечная игра, i ∈ I , Si – множество чистых стратегий игрока i , σi ∈ Σi – смешанная стратегия игрока i . Носителем смешанной стратегии σi называется множество Si+(σi) = { si ∈ Si | σi(si) > 0 }.

Полностью смешанные стратегии (completely mixed strategies) ⊐ G = {I ; S ; U} – конечная игра, i ∈ I; Si – множество чистых стратегий игрока i, σi ∈ Σi – смешанная стратегия игрока i. Стратегия σi называется полностью смешанной, если Si+(σi) = Si .

Равновесие по Нэшу в смешанных стратегиях (mixed Nash equilibrium) ⊐ G = {I ; S ; U} – конечная игра n игроков; Γ = {I ; Σ ; U} смешанное расширение G ; σ∗ = (σ∗1 , σ∗2 , … , σ∗n) ∈ Σ = Σ1 × Σ2 × … ×Σn . Набор стратегий σ∗ называется равновесием по Нэшу в смешанных стратегиях для игры G, если для ∀ i ∈ I ui (σ∗i , σ∗–i) ≥ ui (σi , σ∗–i) для ∀ σi ∈ Σi , т.е. если σ∗ является равновесием по Нэшу для игры Γ.

Характеризация равновесия по Нэшу в смешанных стратегиях ⊐ G = {I ; S ; U} – конечная игра n игроков; Γ = {I ; Σ ; U} – смешанное расширение G ; σ∗ = (σ∗1 , σ∗2 , … , σ∗n) ∈ Σ. Набор σ∗ является равновесием по Нэшу в смешанных стратегиях для игры G тогда и только тогда, когда для ∀ i ∈ I ui (s'i , σ∗–i) = ui (s''i , σ∗–i) для ∀ s'i , s''i ∈ Si+(σi) , ui (s'i , σ∗–i) ≥ ui (s''i , σ∗–i) для ∀ s'i ∈ Si+(σi) и для ∀ s''i ∉ Si+(σi).