Дифференциальным уравнением презентация
Содержание
- 2. Дифференциальным уравнением (ДУ) называется уравнение, содержащее производные от искомой функции или
- 3. Примеры ДУ:
- 4. Наивысший порядок производной, входящей в уравнение, называется порядком ДУ. Наивысший порядок
- 5. Пример 1. Показать, что данная функция является решением
- 6. Решение: Т.о. функции вида являются решениями данного ДУ при
- 7. Дифференциальные уравнения I порядка
- 8. Общим решением ДУ I порядка называется функция , которая зависит от одного
- 9. Частным решением ДУ I порядка называется любая функция полученная из общего
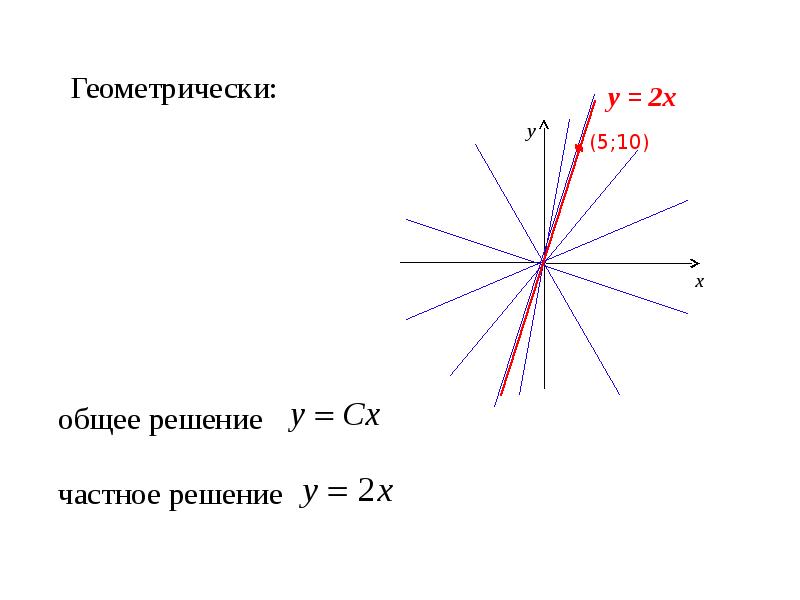
- 10. Пример 2. ДУ:
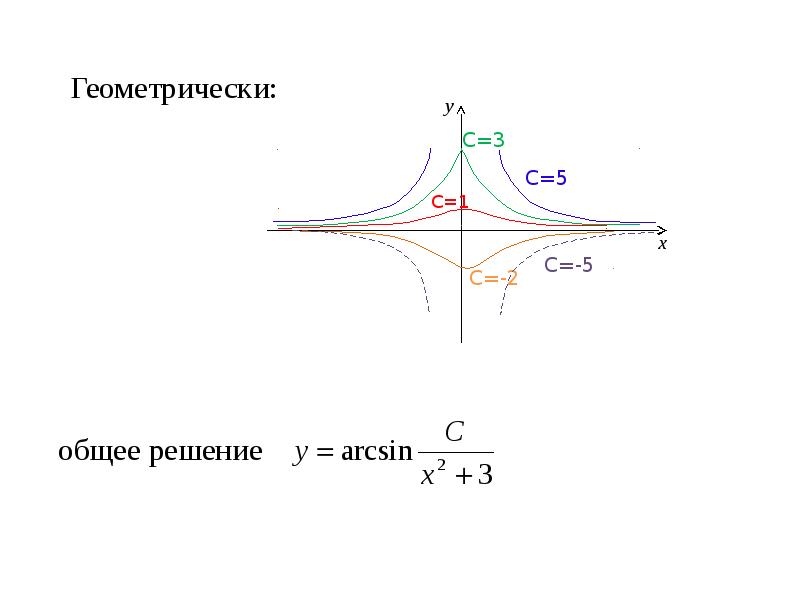
- 11. Геометрически: Общее решение ДУ есть семейство интегральных кривых на плоскости Оху;
- 12. Задача отыскания конкретного частного решения данного ДУ по начальным данным называется
- 13. Пример 3. Решить задачу Коши:
- 14. Теорема существования и единственности решения задачи Коши. Если в уравнении функция
- 15. 1. ДУ I порядка с разделёнными переменными. Если каждая часть ДУ
- 16. Пример 4. Решить ДУ:
- 17. Пример 5. Решить ДУ:
- 18. 2. ДУ I порядка с разделяющимися переменными. Уравнения, в которых переменные
- 20. Замечание: При проведении почленного деления ДУ на могут быть
- 21. Пример 6. Найти общее и частное решение ДУ:
- 24. Пример 7. Найти общее решение ДУ:
- 27. Пример 8. Найти общее решение ДУ:
- 30. Пример 9. Решить задачу Коши:
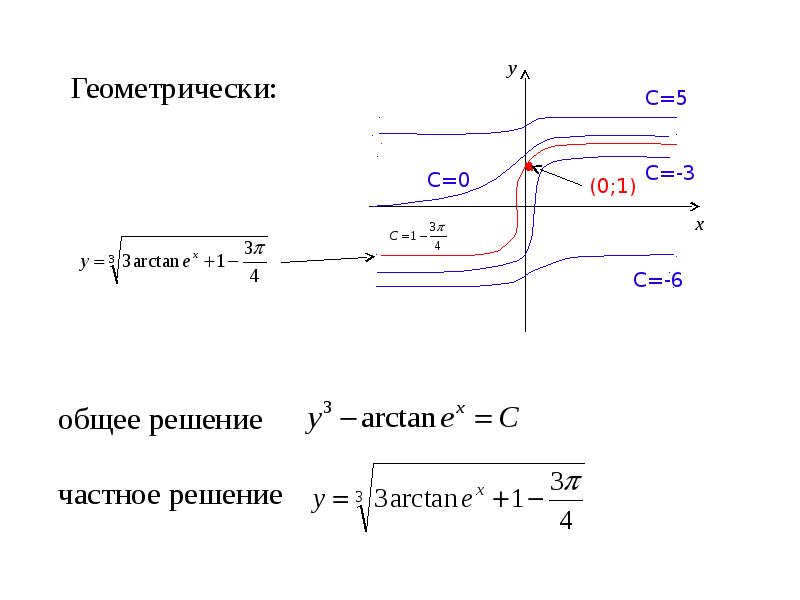
- 34. Пример 10. Решить задачу Коши:
- 38. Скачать презентацию


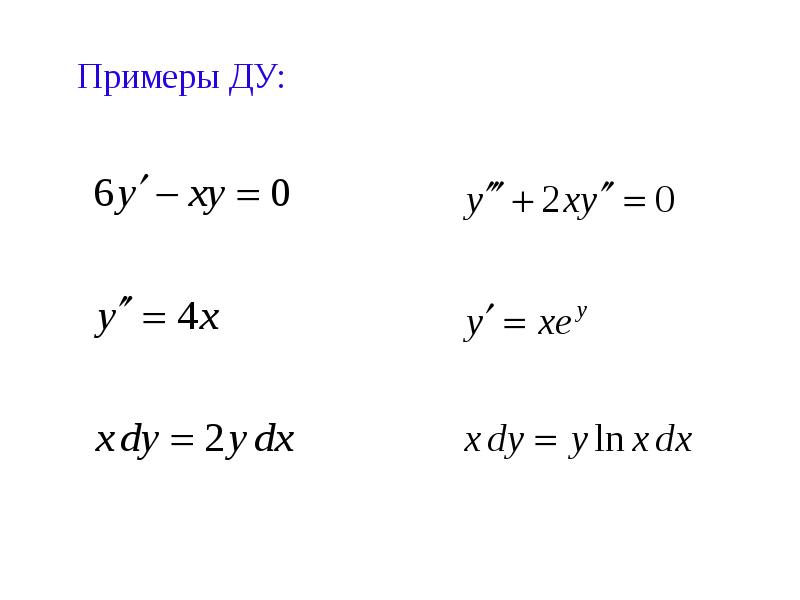















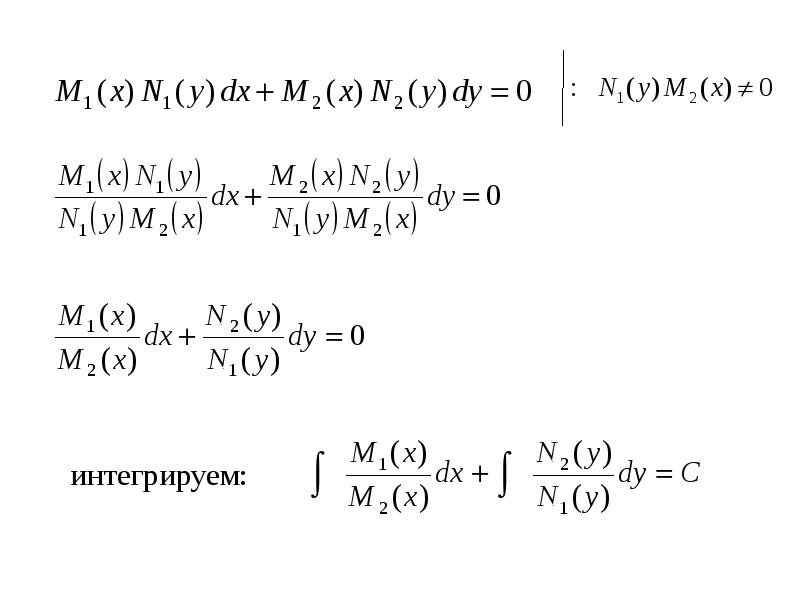




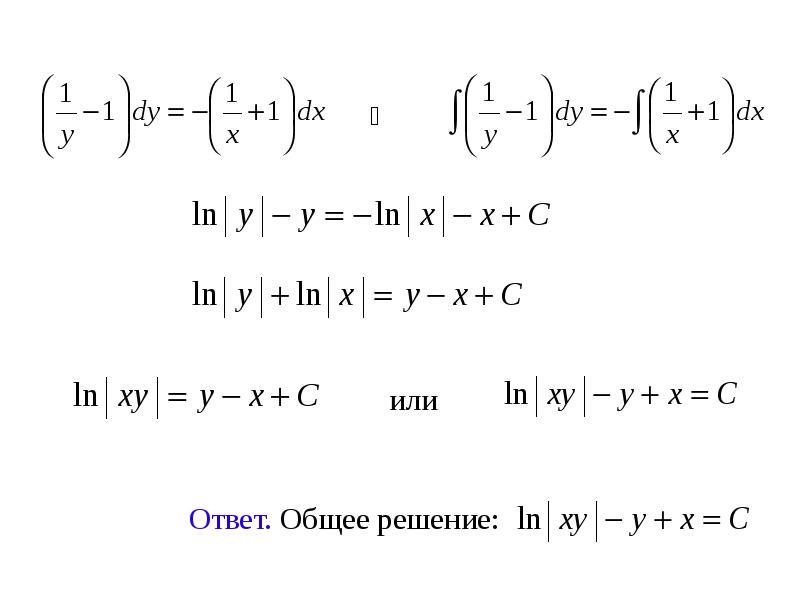







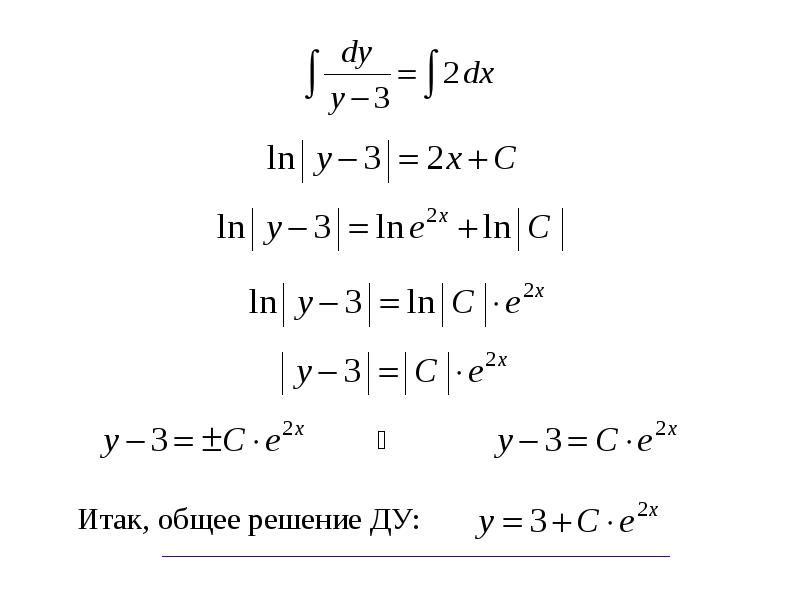


Слайды и текст этой презентации
Похожие презентации





























