Элементы символической логики презентация
Содержание
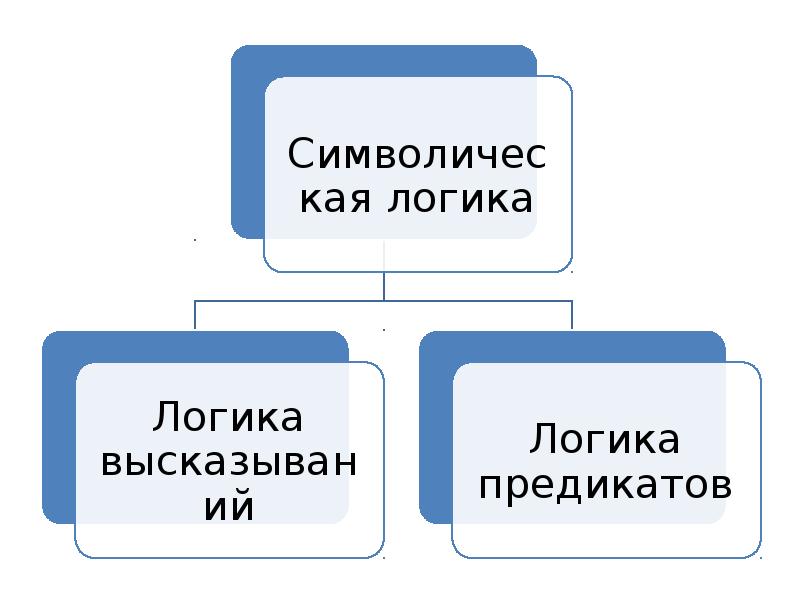
- 2. Символическая логика она же символическая формируется в XIX веке, благодаря
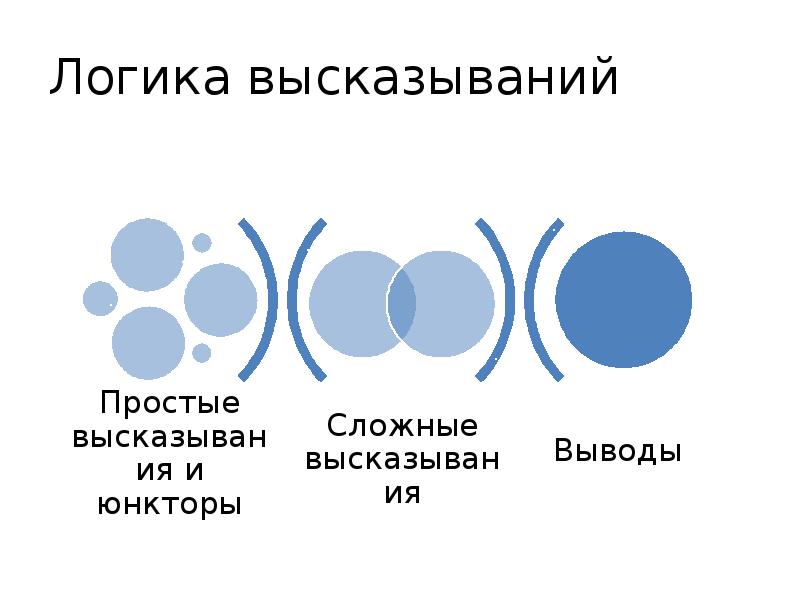
- 4. Логика высказываний
- 5. Высказывание мысль, выраженная повествовательным предложением, которая может быть истинной или ложной
- 6. Формальный аппарат А, В, С…. – пропозициональные переменные (формулы), отражающие независимый
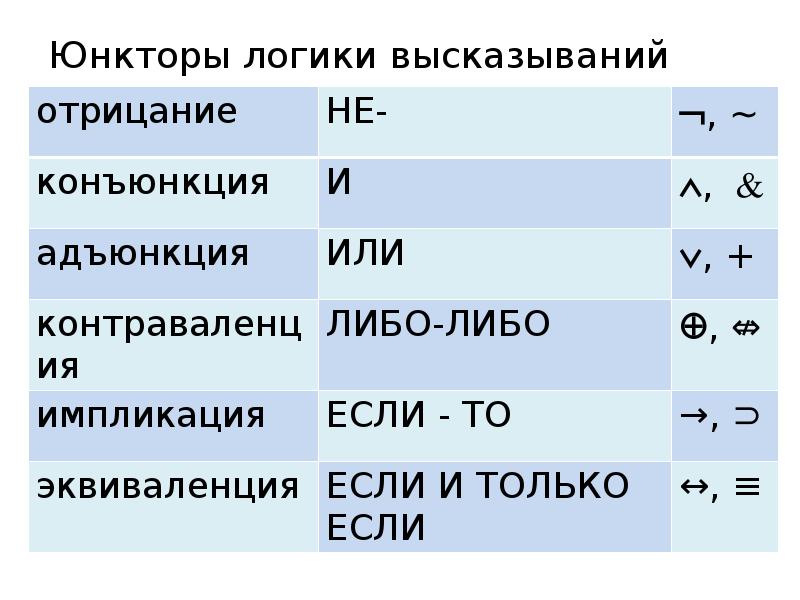
- 7. Юнкторы логики высказываний
- 8. Преобразование конъюнкции в дизъюнкцию (А В) = (А В)
- 9. Преобразование дизъюнкции в конъюнкцию (А В) = (А В)
- 10. Преобразование импликации в конъюнкцию (А → В) = (А В)
- 11. Преобразование строгой дизъюнкции в конъюнкцию (А В) = (А
- 13. Правило подстановки любую буквенную переменную в символическом выражении можно заменять на
- 14. Законы символической логики
- 15. Закон ассоциативности (А (В С)) = ((А В)
- 16. Закон дистрибутивности для двух переменных (А (В С))
- 17. Закон двойственности для конъюнкции и дизъюнкции (А В) = (А
- 18. Закон контрапозиции (А → В) = (А → В) ((А
- 19. Закон транспозиции ((А В) → С) = ((А С)
- 20. Закон поглощения (А (А В)) = А (А
- 21. Логика предикатов результат реконструкции естественного языка Здесь есть точные правила построения
- 23. Имена обозначают отдельный объект, бывают простые и сложные. Простые не
- 24. Предметные функторы знаки так называемых предметных функций (функциональная константа) Наряду с
- 25. Предикатор (предикатная константа) - выражение языка (слова и словосочетания), предметными значениями
- 26. Язык логики предикатов
- 27. Определение терма
- 28. Пример а – «Аполлон» в – «Венера» f1 –
- 29. Определение формулы
- 30. Область действия квантора Если формула А имеет вид хВ или хВ,
- 31. Пример «Если целое число больше 13, то его квадрат делится без
- 32. Некоторые законы логики предикатов 1. Взаимовыразимость кванторов хА хА, хА
- 33. Некоторые законы логики предикатов 4. Законы пронесения и вынесения кванторов а)
- 34. Примеры «Все люди интересуются строением космоса», х(Р1(х) Q1(х, f(a)) где
- 35. Исчисление естественного вывода порождение одних формул из других Здесь нет
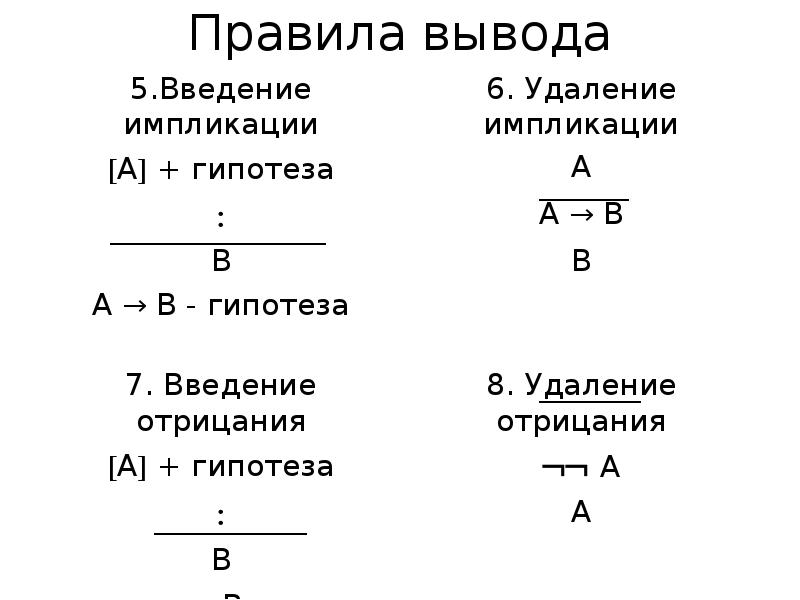
- 36. Правила вывода
- 37. Правила вывода
- 38. Пример
- 39. Спасибо за внимание
- 40. Скачать презентацию



































Слайды и текст этой презентации
Похожие презентации





























