Элементы теории множеств. Понятие множества презентация
Содержание
- 2. Основу теории математики составляют понятия и отношения между этими понятиями, которые
- 3. Определение Одним из фундаментальных, неопределяемых математических понятий является понятие множества.
- 4. Определение Предметы, из которых состоит множество, называются его элементами например, буква
- 5. Обозначают множества заглавными буквами латинского алфавита или символически с помощью фигурных
- 6. Принадлежность предмета некоторому множеству обозначают с помощью символа (в противном
- 7. Основными способами задания множества являются: Основными способами задания множества являются: 1)
- 8. Например, характеристическим свойством натуральных чисел является возможность их использования при счете
- 9. Определение 3 Определение 3 Множества, состоящие из одних и
- 10. Слово «много» и математический термин «множество» имеют различный смысл. Слово
- 11. Подмножество. Основные числовые множества Определение 1. Множество В, состоящее из некоторых
- 12. Если в множестве В найдется хотя бы один элемент, не принадлежащий
- 13. Из опр. 1 следует, что любое множество является подмножеством самого себя,
- 14. Знак называется знаком включения. Знак называется знаком включения.
- 15. Основные числовые множества: N={1,2,3,4,…} – множество натуральных чисел; Z={…,-4,-3,-2,-1,0,1,2,3,4,…} – множество
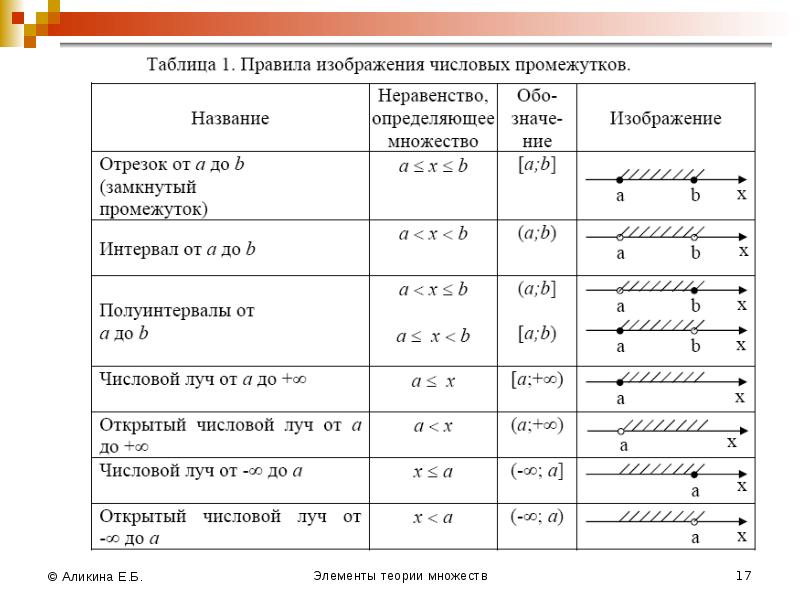
- 16. Действительные числа изображаются точками координатной прямой (числовой оси). Действительные числа
- 18. Операции над множествами Два множества могут иметь одинаковые элементы, из всех
- 19. Например, А – множество наклеек (марок), которые есть у Пети, В
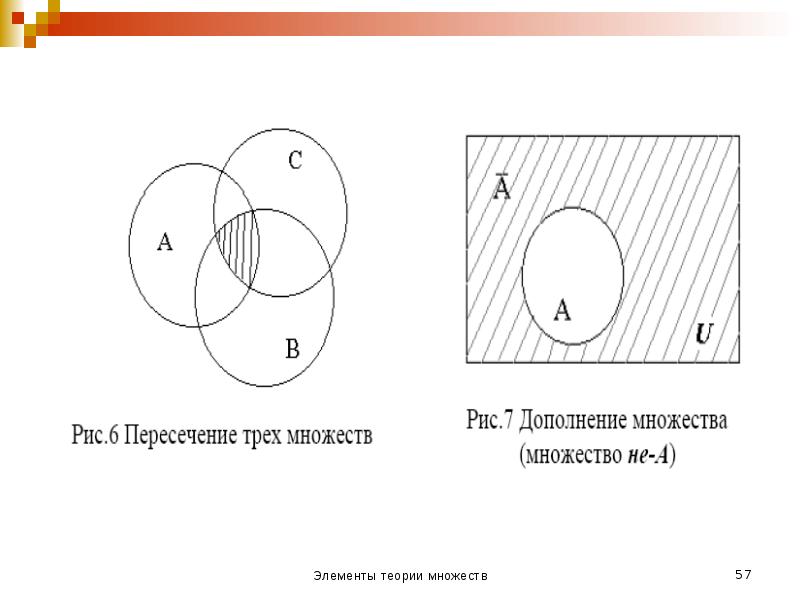
- 20. Определение Пересечением множеств А и В называется множество С, состоящее из
- 21. Определение Объединением множеств А и В называется множество С, которое состоит
- 22. Если множества А и В не содержат одинаковых элементов, т.е. не
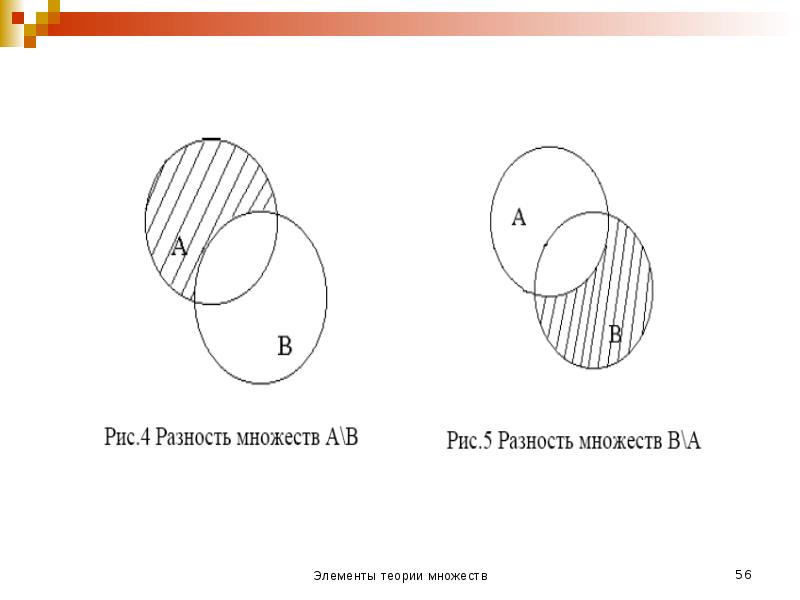
- 23. Определение Разностью множеств А и В называется множество С, состоящее из
- 24. Определение Универсальным множеством называется множество, подмножества которого (и только они) в
- 25. Определение Дополнением множества А называется разность U\А.. Обозначается, А’ или А
- 27. Бесконечные множества. Взаимно-однозначное соответствие. Взаимно-однозначным называется такое соответствие между множествами A
- 28. Бесконечные множества. Эквивалентные множества. Множества A и B называются эквивалентными (AB),
- 29. Бесконечные множества. Счетные множества Множество A называется счетным, если оно эквивалентно
- 30. Бесконечные множества. Счетные множества Множество четных натуральных чисел Nч={2,4,…,m,…}, всех натуральных
- 31. Бесконечные множества. Несчетные, континуальные множества Существуют бесконечные несчетные множества, и их
- 32. Бесконечные множества. Континуальные множества На вещественной оси R континуальными (и значит
- 33. СВОЙСТВА СЧЕТНЫХ МНОЖЕСТВ Всякое подмножество счетного множества конечно или счетно. Подмножеством
- 34. Для каждого множества А существуют множества, элементами которого являются только все
- 35. ТЕОРИЯ МНОЖЕСТВ СТРОИТСЯ НА ОСНОВЕ СИСТЕМ АКСИОМ Аксиома существования: Существует по
- 36. Диаграммы Эйлера-Венна Для наглядного представления множеств и результатов операций над ними
- 37. Диаграммы Венна для двух множеств Диаграмма Венна для двух множеств A
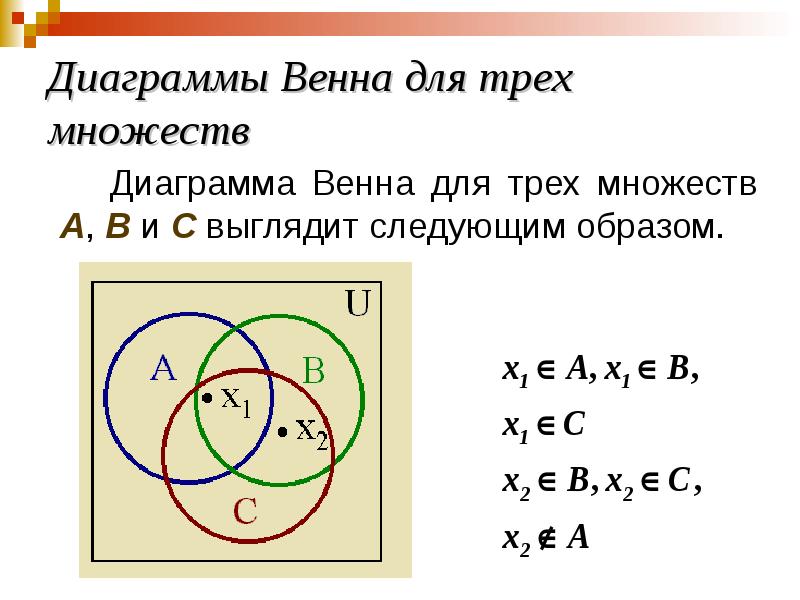
- 38. Диаграммы Венна для трех множеств Диаграмма Венна для трех множеств A,
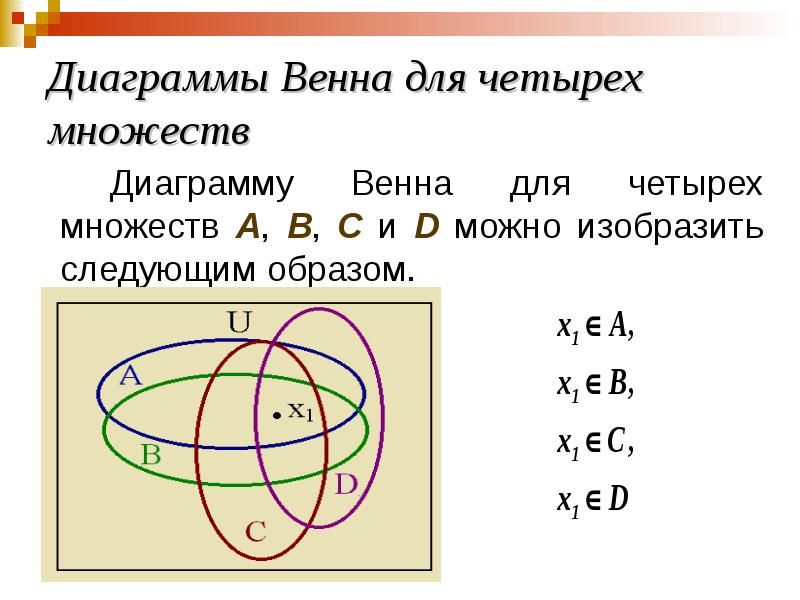
- 39. Диаграммы Венна для четырех множеств Диаграмму Венна для четырех множеств A,
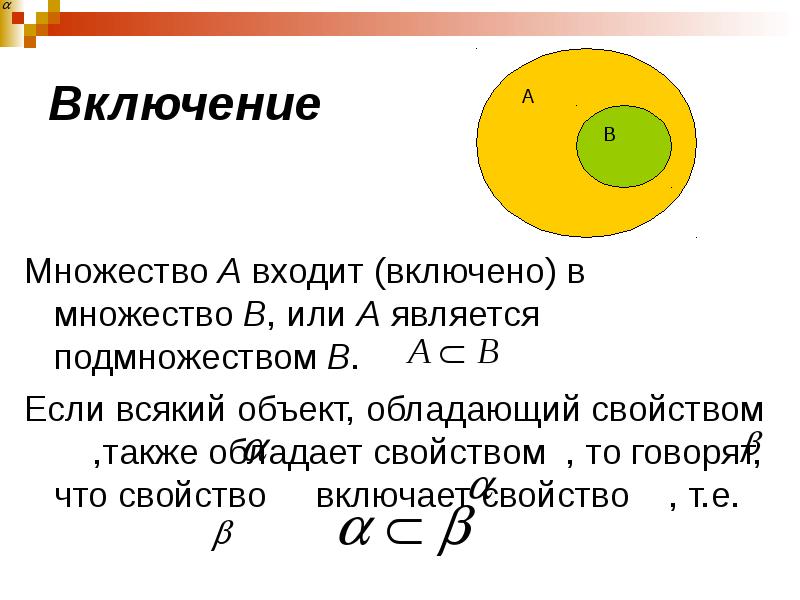
- 40. Включение Множество А входит (включено) в множество В, или А является
- 41. Строгое и нестрогое включение Нестрогое включение обозначается АВ, означает, что А
- 42. Строгое и нестрогое включение. Равенство множеств Выполнение соотношений А В
- 43. Строгое и нестрогое включение Пример. X – множество студентов группы 4141133,
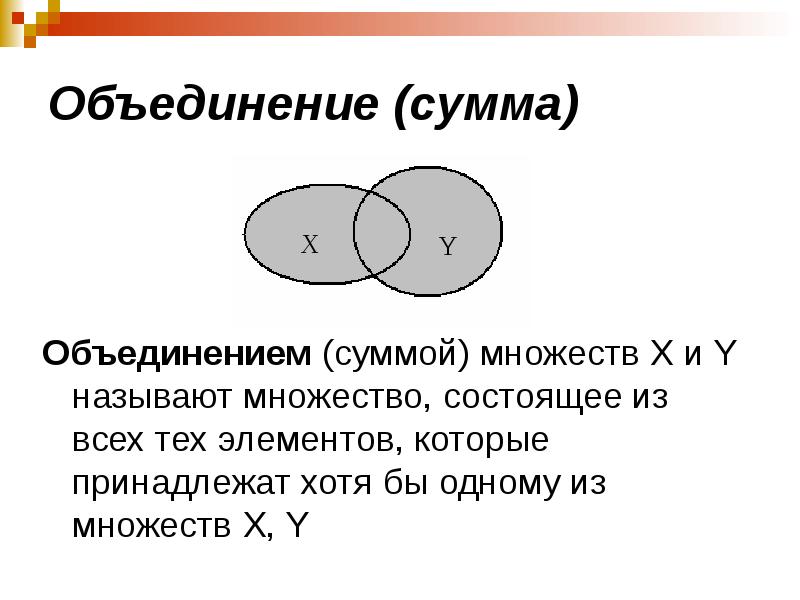
- 44. Объединение (сумма) Объединением (суммой) множеств X и Y называют множество,
- 45. Сумма Сумма множеств А и В есть множество С, включающее в
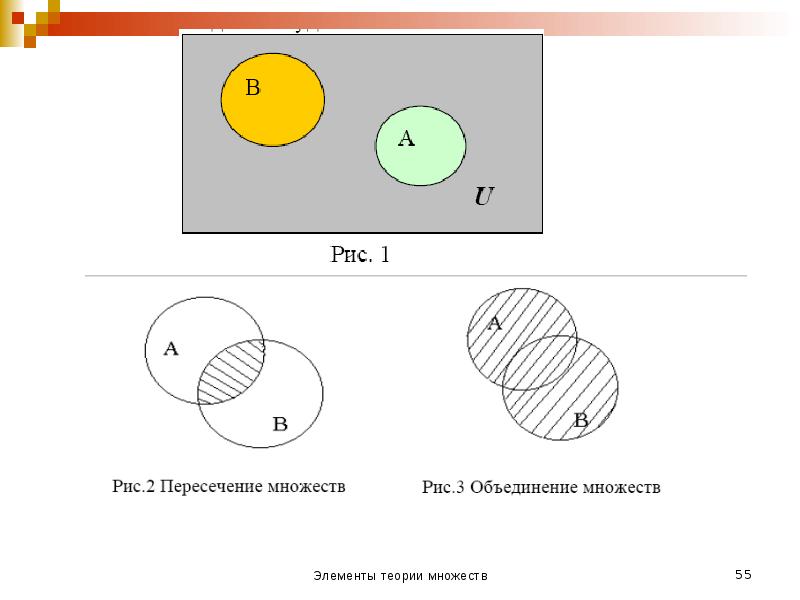
- 46. Пересечение (произведение) Пересечением множеств X и Y называют множество, состоящее из
- 47. Пересечение множеств обозначается через X Y. Множества X и Y называют непересекающимися,
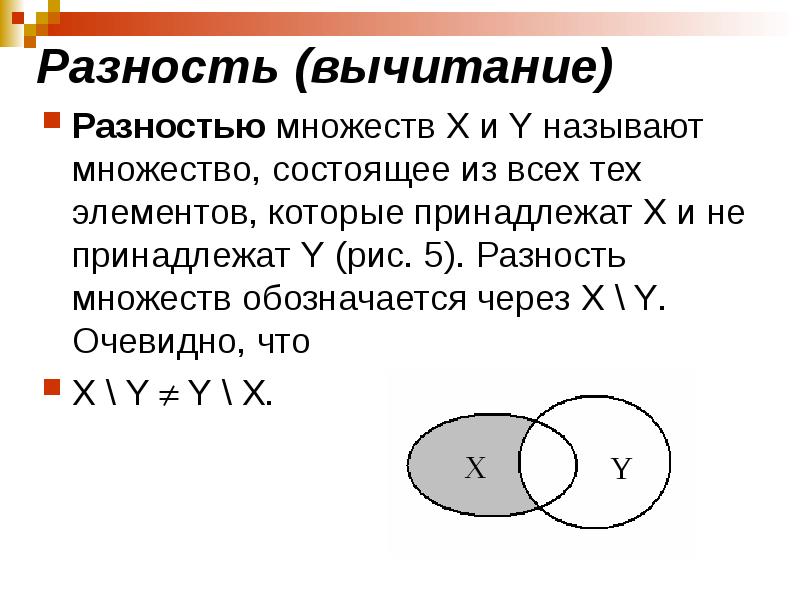
- 48. Разность (вычитание) Разностью множеств X и Y называют множество, состоящее из
- 49. Разность множеств А и В есть множество С, элементы которого обладают
- 50. Симметрическая разность Симметрической разностью X Y (X Δ Y) множеств X и Y называется
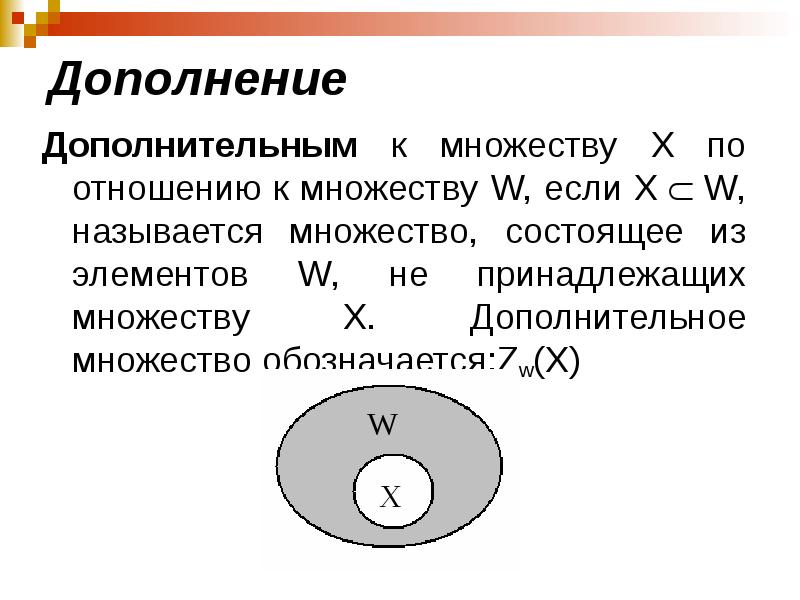
- 51. Дополнение Дополнительным к множеству X по отношению к множеству W, если
- 52. Если имеется некоторое универсальное множество (универсум) U и все рассматриваемые множества
- 53. Универсальное множество Универсальным множеством называется множество I, для которого справедливо
- 54. Круги Эйлера Индивидуальные отношения между заданными множествами изображают с помощью
- 58. Законы алгебры множеств 1. Коммутативные законы AB=BA AB=BA 2. Ассоциативные законы
- 59. Законы алгебры множеств 4. Свойства пустого и универсального множеств
- 60. Законы алгебры множеств 5. Законы идемпотентности AA=A AA=A 6. Закон инволюции
- 61. Законы алгебры множеств 9. Закон элиминации (поглощения) A(AB)=A A(AB)=A 10.
- 62. Примеры Пример 1. Записать множество всех натуральных делителей числа 15 и
- 63. Пример 2 Даны множества А={2, 3, 5, 8, 13, 15}, В={1,
- 64. Пример 3. Экзамен по математике сдавали 250 абитуриентов, оценку ниже пяти
- 65. Пример 4. В школе 1400 учеников. Из них 1250 умеют кататься
- 67. Учащиеся, не умеющие кататься ни на лыжах, ни на коньках, составляют
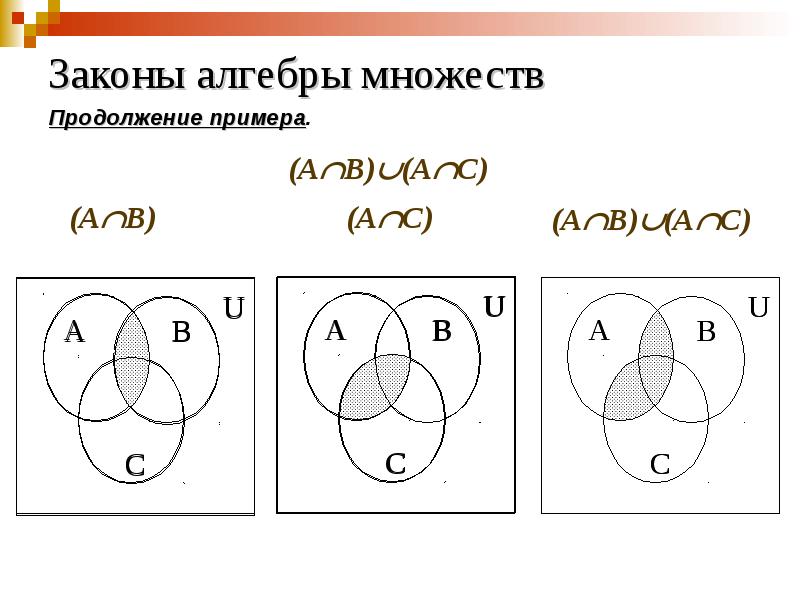
- 69. Законы алгебры множеств Пример. Доказать с помощью диаграмм Венна дистрибутивный закон.
- 70. Законы алгебры множеств Продолжение примера.
- 71. Законы алгебры множеств Продолжение примера.
- 72. Скачать презентацию


























































Слайды и текст этой презентации
Скачать презентацию на тему Элементы теории множеств. Понятие множества можно ниже:
Похожие презентации





























