Фундаментальные циклы презентация

Фундаментальные циклы (продолжение)

Структуры данных Граф задаем матрицей смежности. Для отметки проходимых вершин используем массив Chk[N]. Для хранения проходимых вершин используем стек.

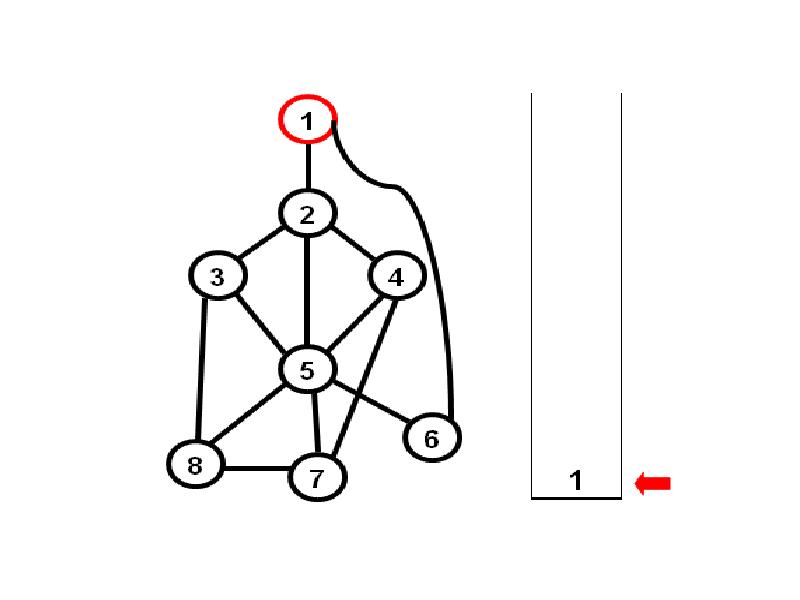
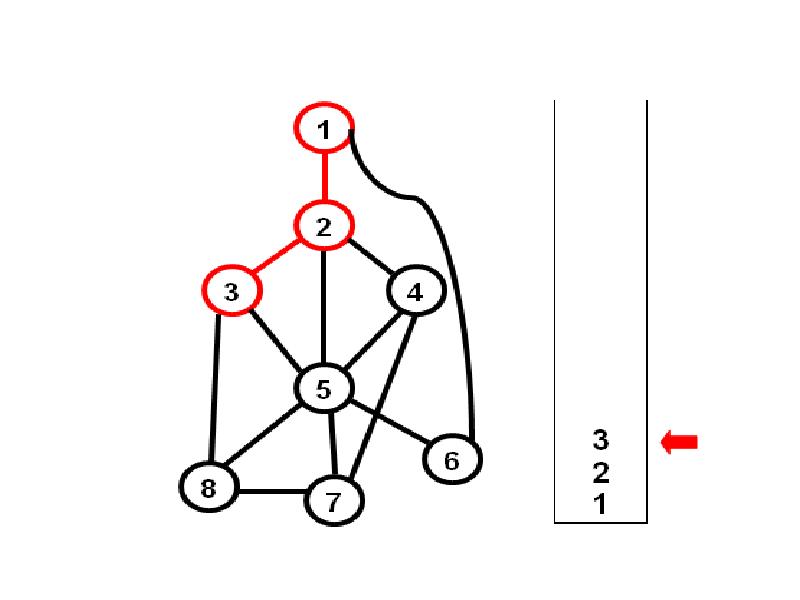
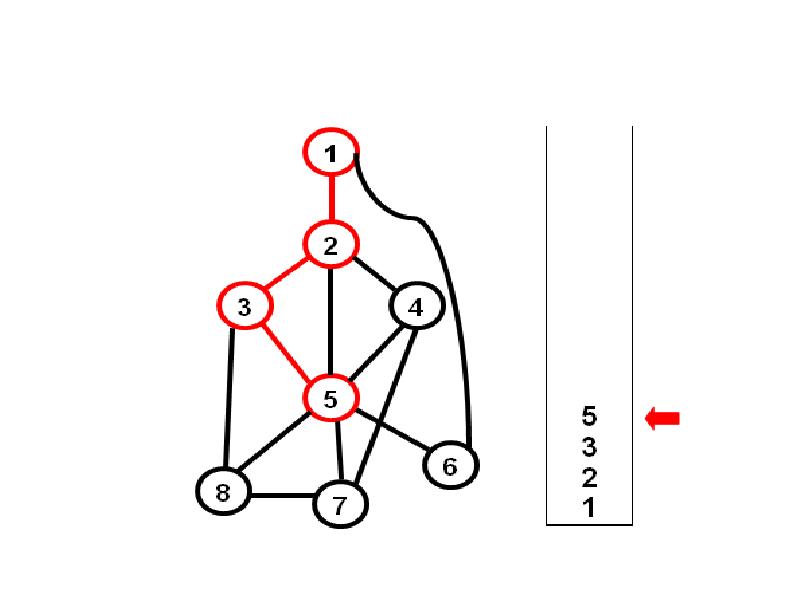
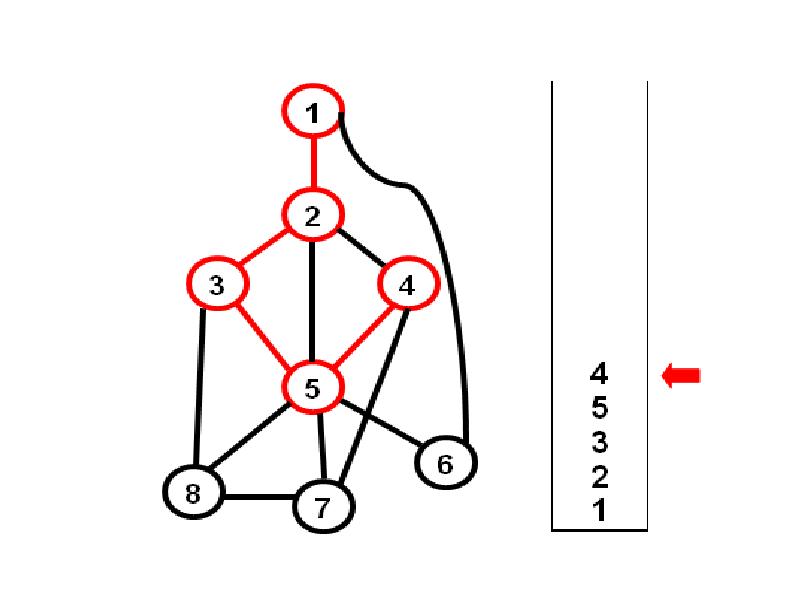
Алгоритм обхода в глубину 1) Берем произвольную начальную вершину, и заносим ее в стек; 2) Стек пуст? Если ДА – конец; 3) Берем вершину Z из стека; 4) Если есть вершина Q, связанная с Z и не отмеченная, то возвращаем Z в стек, заносим в стек Q, печатаем ребро (Z,Q); 5) Переходим к п.2

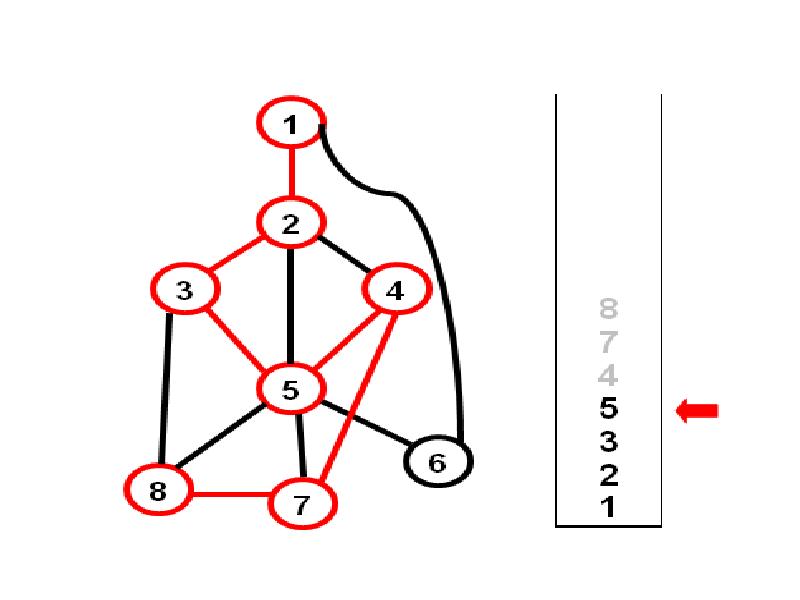
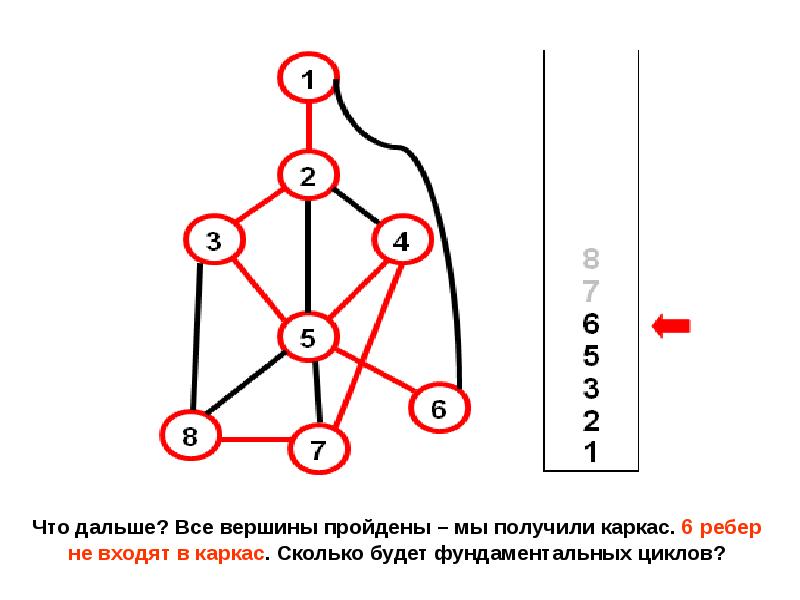
Как программно построить фундаментальные циклы?

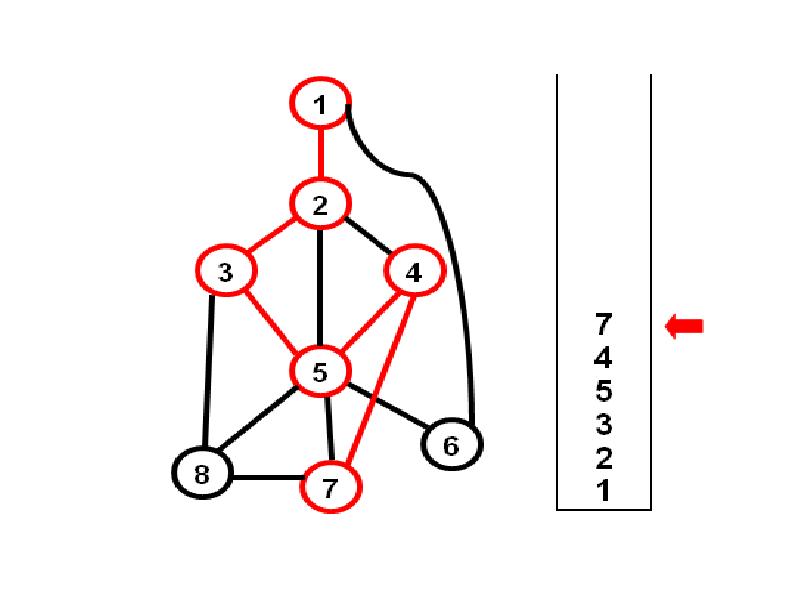
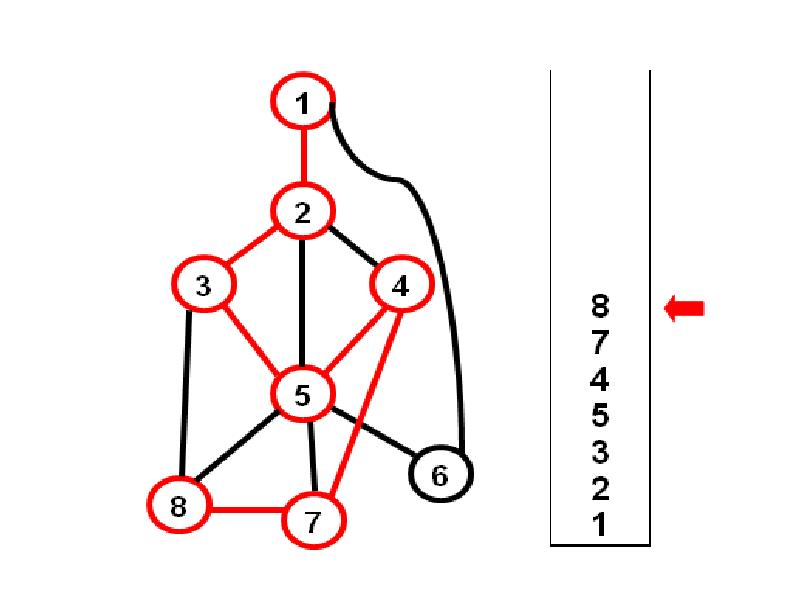
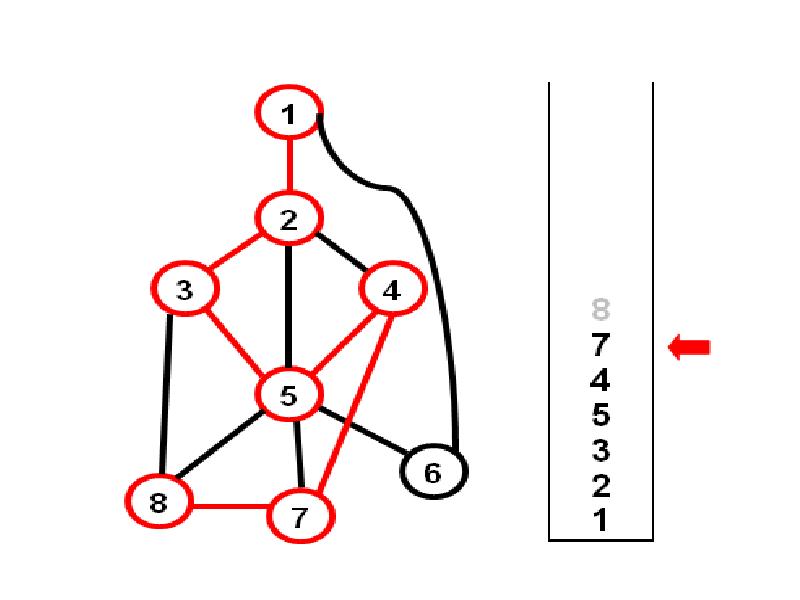
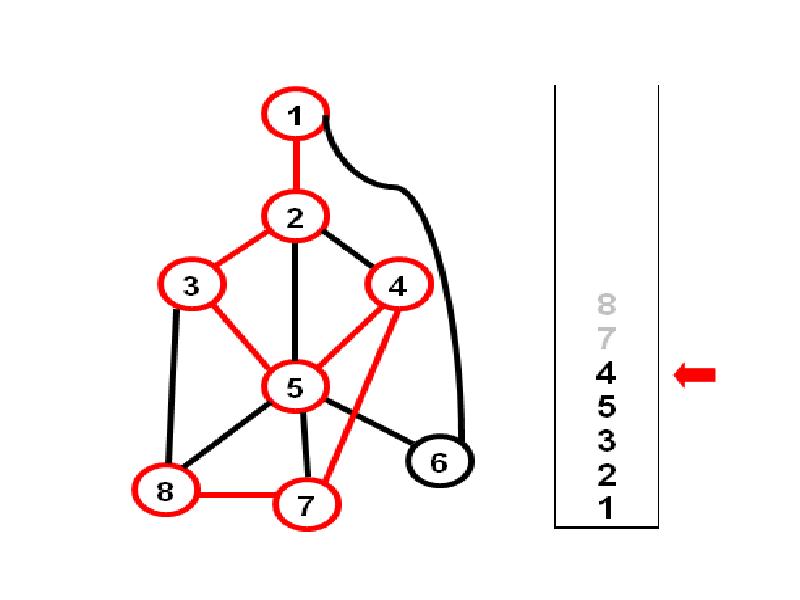
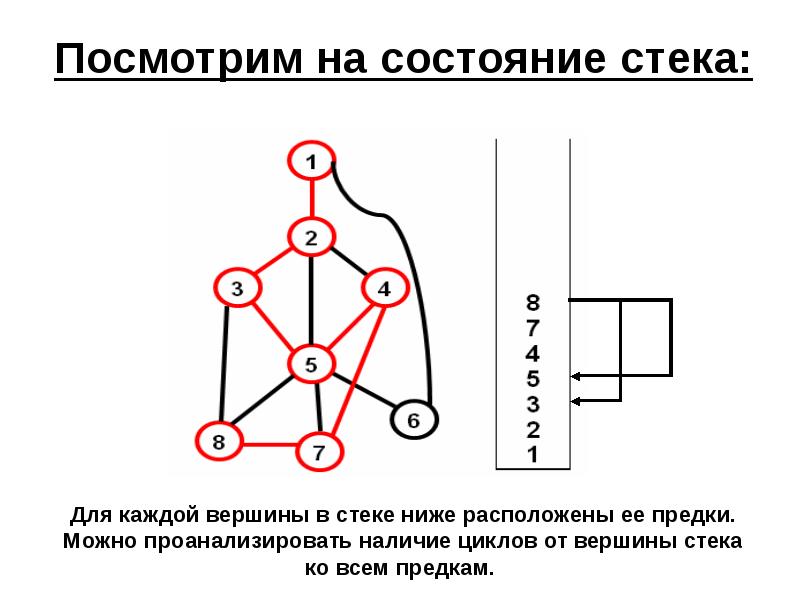
Посмотрим на состояние стека:

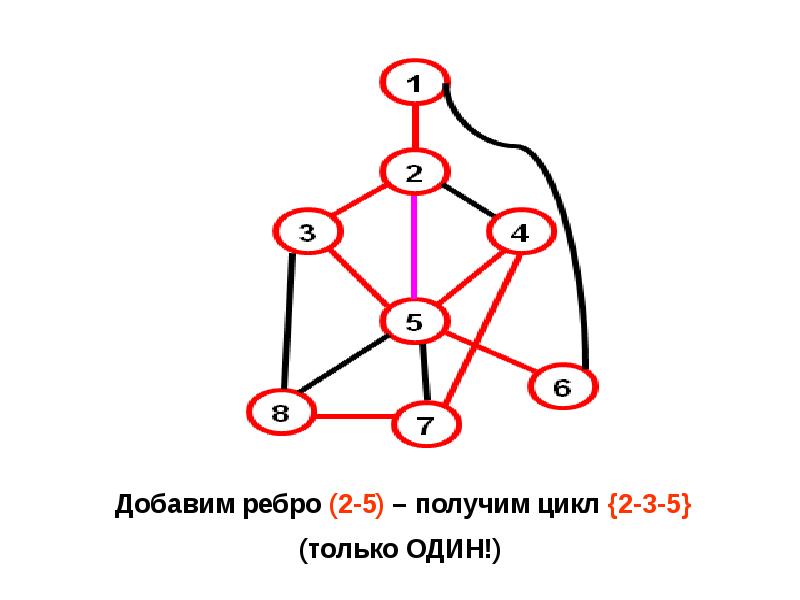
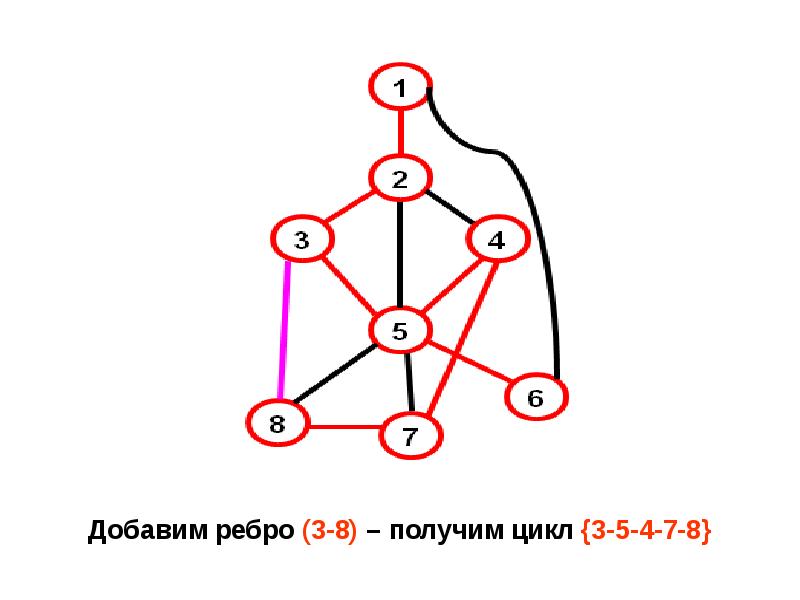
Алгоритм генерации циклов параллельно с поиском в глубину Добавив в стек очередную вершину Z, нужно пройтись по стеку от вершины к началу, проверяя (по матрице смежности) нет ли в графе ребра (Z,C). (C – вершина в стеке, расположенная ниже Z.) Если ребро есть – печатаем отрезок стека от Z до C.

Просмотр стека нужно начинать с вершины, лежащей на 2 позиции ниже вершины. Просмотр стека нужно начинать с вершины, лежащей на 2 позиции ниже вершины.

Программная реализация построения фундаментального множества циклов

void ChkLoop() // Проверка стека на наличие циклов void ChkLoop() // Проверка стека на наличие циклов { int i,j,C,k; i=sPtr-1; // i указывает на верхний элемент стека if (i <= 1) return; // Если в стеке мало вершин - выход C=sArr[i]; // C – вершина, добавленная последней for (j=i-2; j >= 0; j--) // Ищем связь с одной из более глубоких // вершин if (isBound(C,sArr[j])) // Нашли – печатаем найденный цикл { cout << "Loop: "; for (k=j; k<=i; k++) cout << sArr[k] << " "; cout << endl; } }

void Show() // Вывод состояния стека void Show() // Вывод состояния стека { int i; cout << "STACK: "; for (i=0; i < sPtr; i++) cout << sArr[i] << " "; cout << endl; }

int main(int argc, char* argv[]) int main(int argc, char* argv[]) { int i,j,n; char fnam[200]; FILE *inp; if (argc < 2) { cout << "Enter file name: "; cin >> fnam; } else strcpy(fnam,argv[1]); if ((inp=fopen(fnam,"r")) == NULL) { cout << "Error by open..." << endl; return 0; } else { fscanf(inp,"%d",&n); // Ввод размера стека и его создание cout << "Stack size=" << n << endl; InitStack(n);

// Ввод числа вершин графа // Ввод числа вершин графа fscanf(inp,"%d",&n); cout << "Number of nodes=" << n << endl; // Создание матрицы смежности InitGraph(n); while (1) // Задание ребер графа { if (fscanf(inp,"%d %d", &i, &j) == EOF) break; if ((i <= n) && (j <= n) && (i > 0) && (j > 0)) SetBound(i,j); else cout << "Bad node numbers: " << i << " " << j << endl; } // Построение стягивающего дерева и генерация циклов try { DFS(); } catch (char *error_message) { cout << error_message << endl; }

// Завершение... // Завершение... fclose(inp); DestroyStack(); delete Matr; delete Chk; cin >> i; } return 0; }

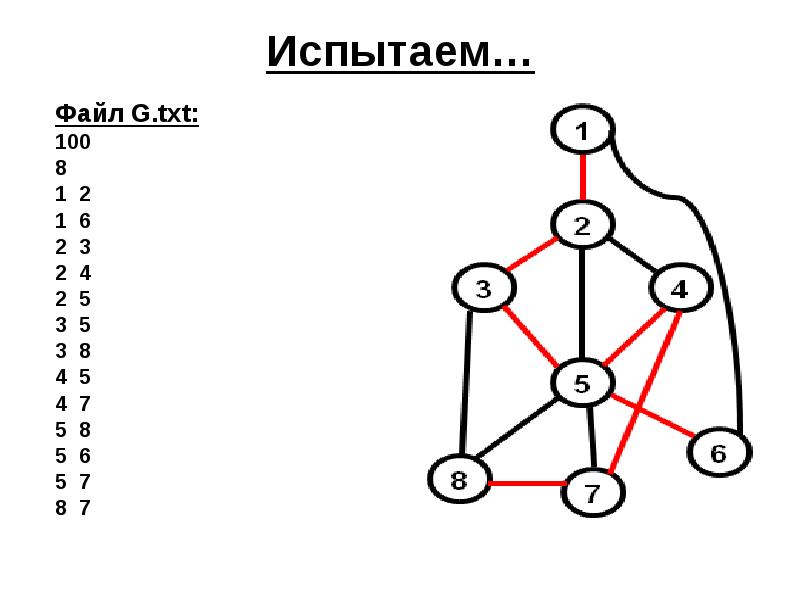
Испытаем… Файл G.txt: 100 8 1 2 1 6 2 3 2 4 2 5 3 5 3 8 4 5 4 7 5 8 5 6 5 7 8 7

Двусвязность

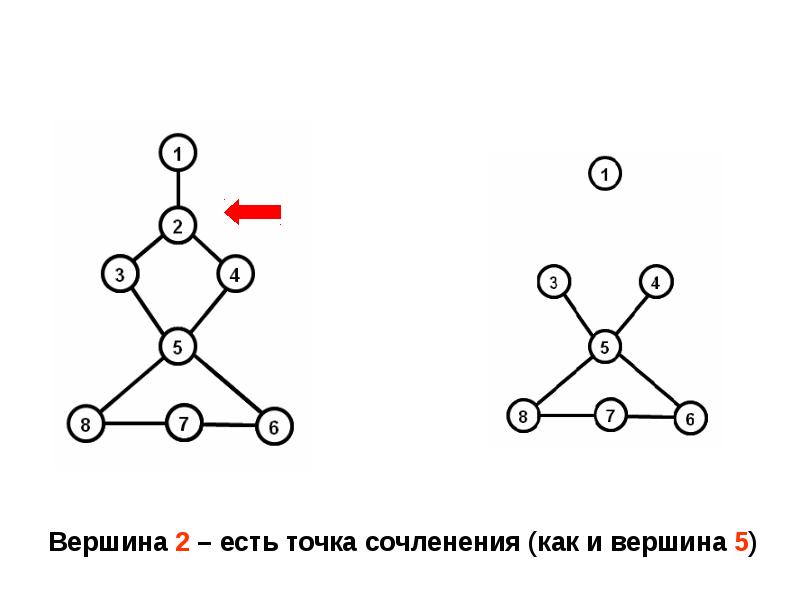
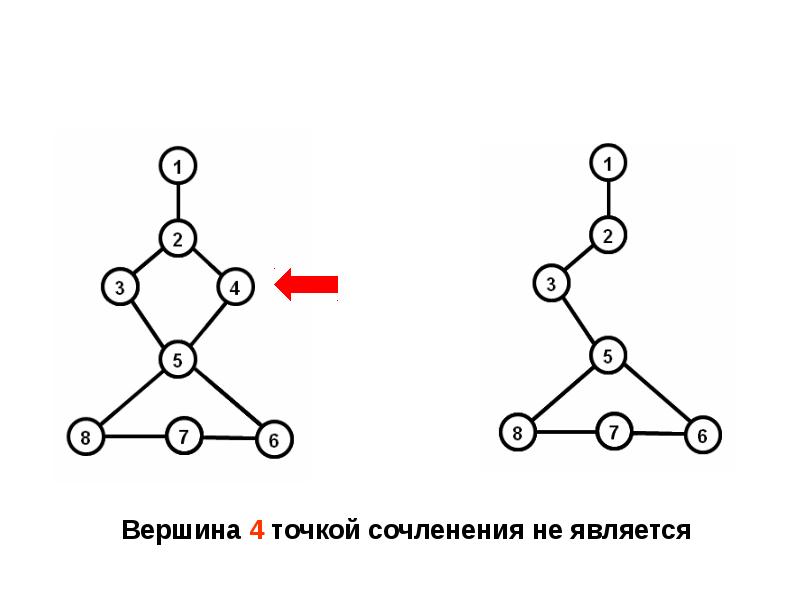
Определение Вершина A неориентированного графа называется точкой сочленения, если удаление этой вершины и всех инцидентных ей ребер ведет к увеличению числа компонентов связности.

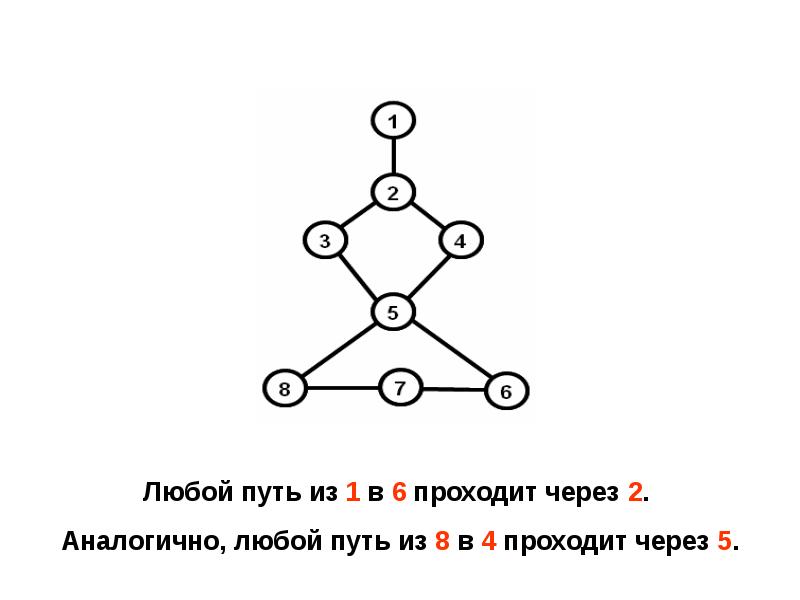
Эквивалентное определение точки сочленения Вершина A есть точка сочленения, если в графе существуют вершины V и U (отличные от A), такие, что любой путь из V в U проходит через A.

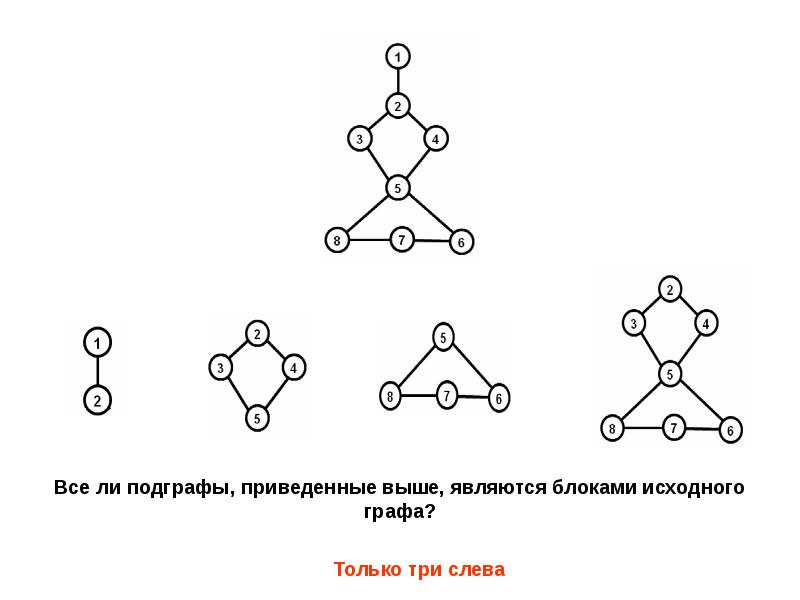
Определение Неориентированный граф называется двусвязным, если он связный и не содержит точек сочленения.

Двусвязность – очень важное свойство графа. Двусвязность – очень важное свойство графа. Расхожий пример: Если граф компютерной сети двусвязен, то исключение любого из узлов не развалит сеть на изолированные блоки.

Интересное свойство блоков Если B1 и B2 – два разных блока графа G, то возможны только два случая: Множество вершин B1 и B2 не пересекаются; Пересечение множества вершин B1 и B2 есть точка сочленения графа G.

Докажем это Если блоки B1 и B2 имеют две или более общие вершины, то граф, получающийся из B1 и B2 объединением множества вершин и ребер, будет двусвязным. Все пути между вершинами блоков B1 и B2 можно провести через одну или другую общую вершину – нет точек сочленения.

Получается, что объединение блоков B1 и B2 двусвязно, что противоречит максимальности блоков B1 и B2. Получается, что объединение блоков B1 и B2 двусвязно, что противоречит максимальности блоков B1 и B2.

Рассмотрим случай, когда блоки B1 и B2 имеют одну общую вершину A. Рассмотрим случай, когда блоки B1 и B2 имеют одну общую вершину A. Если эта вершина A не есть точка сочленения исходного графа G, то для двух вершин v1 (из B1) и v2 (из B2) существует путь в G, не проходящий через A. Добавим к объединению B1 и B2 ребра и вершины этого пути – получим двусвязный граф (включающий B1 и B2). Значит B1 и B2 – не максимальны.

Получается, что блоки могут либо пересекаться по точке сочленения, либо не иметь общих вершин. Получается, что блоки могут либо пересекаться по точке сочленения, либо не иметь общих вершин.

Теорема Пусть T есть стягивающее дерево графа G, построенное методом обхода в глубину и R – корень дерева T. Вершина V есть точка сочленения графа G в одном из двух случаев:  V=R и R имеет по крайней мере двух сыновей в T.  V <>R и существует сын W вершины V, такой, что ни W ни один из его потомков не связаны ребром с предками V.

Доказательство. Рассмотрим сначала случай V=R. Если корень имеет только одного сына, то устранение корня не увеличит число компонент связности. А если сыновей больше одного, то при устранении корня, они окажутся в разных компонентах связности.

Это имеет место потому, что путь между двумя различными сыновьями корня проходит через корень. Это имеет место потому, что путь между двумя различными сыновьями корня проходит через корень. Если бы это было не так, то между двумя сыновьями корня существовал бы путь, содержащий хорду (U,S), где ни U не было бы потомком S, ни S не было бы потомком U

Пусть теперь V<>R. Устраним V. Пусть теперь V<>R. Устраним V. Если после устранения существует путь от W (потомка V) до корня R, то этот путь должен содержать ребро, соединяющее W (или его потомка) с предком V

http://catstail.narod.ru/lec/lec-10.zip