Избранные главы математики презентация
Содержание
- 2. Содержание Основные понятия теории вероятностей Теоремы сложения, умножения вероятностей Формула полной
- 3. Определение. Вероятностью события А называется математическая оценка возможности появления этого события
- 4. Определение. Полной группой событий называется совокупность всех возможных результатов опыта. Определение.
- 5. Определение. Относительной частотой события А называется отношение числа опытов, в результате
- 6. Определение. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают
- 7. Теоремы сложения, умножения вероятностей Теоремы сложения, умножения вероятностей Теорема (сложения вероятностей).
- 8. Определение. Противоположными называются два несовместных события, образующие полную группу. Определение. Противоположными
- 9. Определение. Событие А называется независимым от события В, вероятность события А
- 10. Определение. Вероятность события В, вычисленная при условии, что имело место событие
- 11. Если события независимые, то
- 12. Формула полной вероятности. Формула Бейеса Пусть некоторое событие А может произойти
- 13. Теорема. Вероятность события А, которое может произойти вместе с одним из
- 14. Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания
- 15. Повторение испытаний. Формула Бернулли Если производится несколько испытаний, причем вероятность события
- 16. гдe гдe В частности Вероятность того, что в n
- 17. Cлучайная величина. Законы распределения. Функция распределения Случайной называют величину, которая в
- 18. Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения с
- 19. Закон распределения дискретной случайной величины Законом распределения дискретной случайной величины называют
- 20. Аналитическое задание закона распределения: Биномиальное распределение, определяемое законом Бернулли k =
- 21. Графическое задание закона распределения представлено на рис. 1 Графическое задание закона
- 22. Способ описания распределения случайной величины в виде таблицы, в виде формулы
- 23. Геометрический смысл интегральной функции распределения – это вероятность того, что случайная
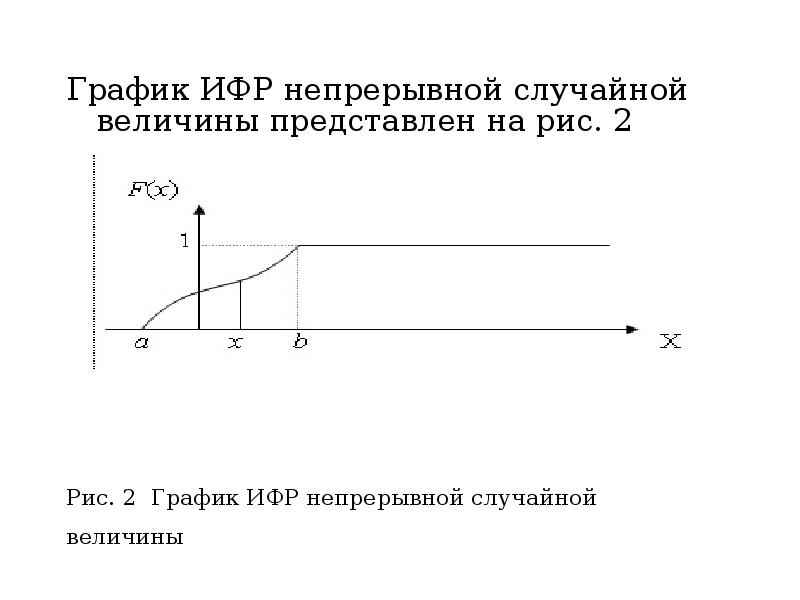
- 24. График ИФР непрерывной случайной величины представлен на рис. 2 График ИФР
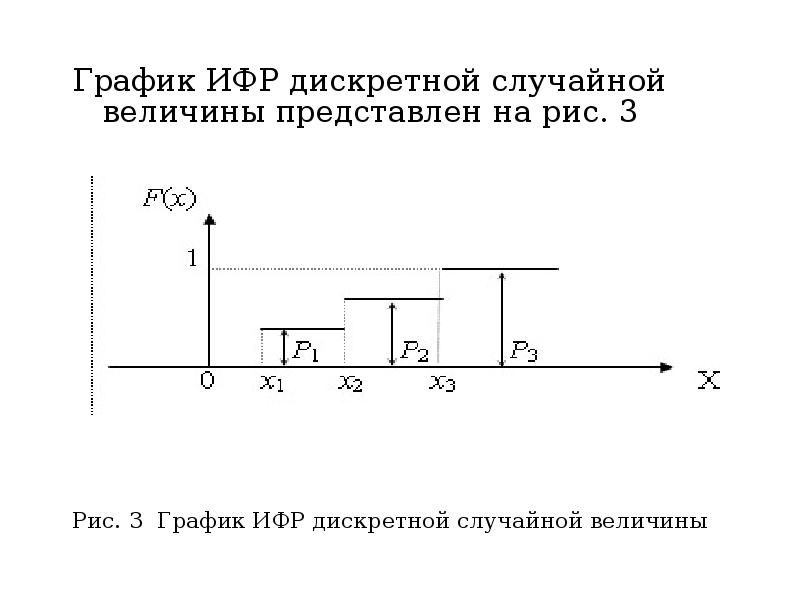
- 25. График ИФР дискретной случайной величины представлен на рис. 3 График ИФР
- 26. Дифференциальная функция распределения Для описания распределения вероятностей непрерывной случайной величины используется
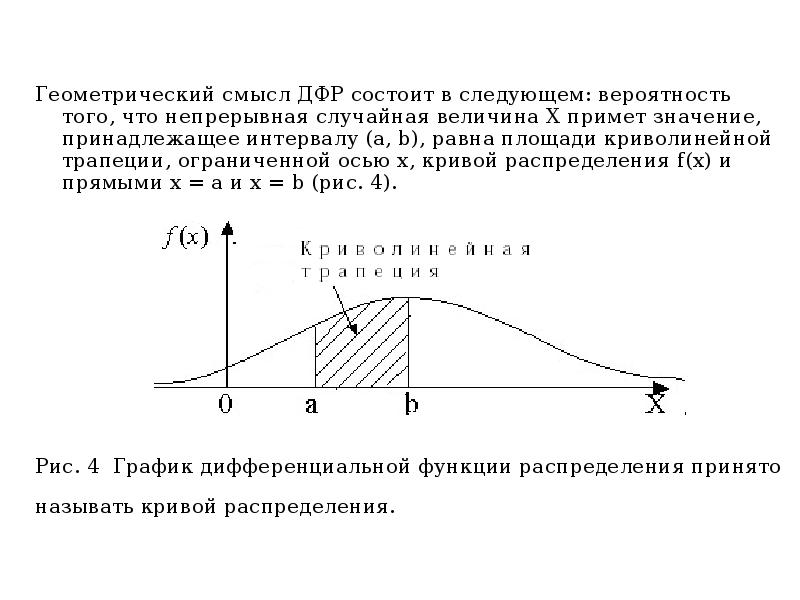
- 27. Геометрический смысл ДФР состоит в следующем: вероятность того, что непрерывная случайная
- 28. Свойства дифференциальной функции распределения: 1. Дифференциальная функция распределения неотрицательна, т. е.
- 29. При решении прикладных задач сталкиваются с различными законами распределения вероятностей непрерывных
- 30. Равномерное распределение непрерывной случайной величины Закон равномерного распределения вероятностей непрерывной
- 31. Распределение вероятностей называют равномерным, если на интервале (a,b), которому принадлежат все
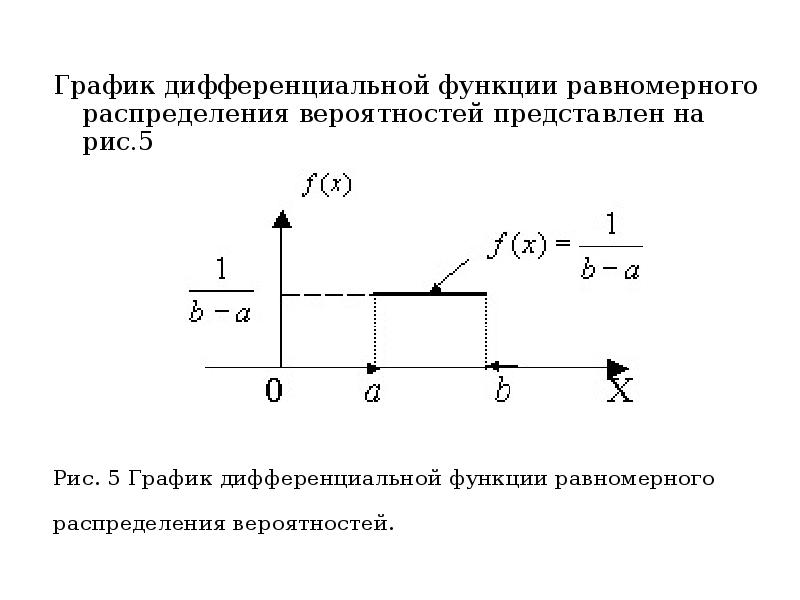
- 32. График дифференциальной функции равномерного распределения вероятностей представлен на рис.5 График дифференциальной
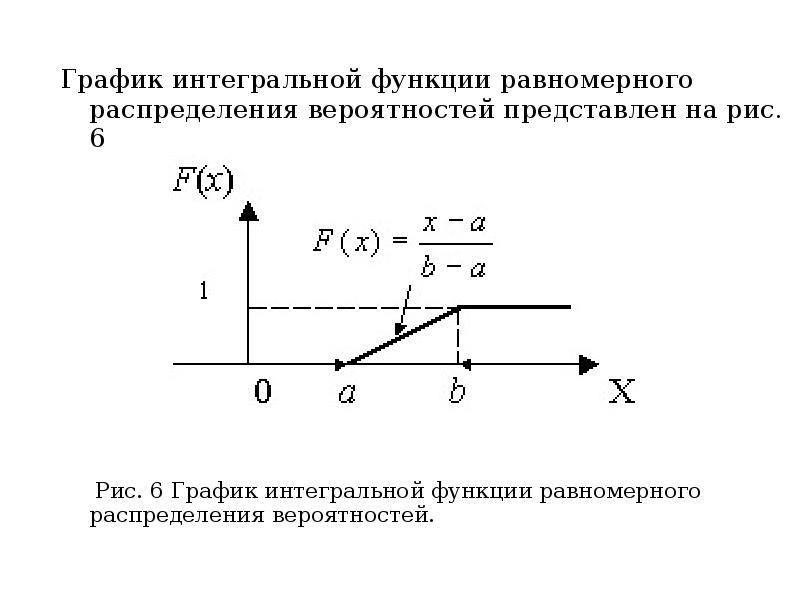
- 33. Интегральную функцию равномерного распределения аналитически можно записать так: Интегральную функцию равномерного
- 34. График интегральной функции равномерного распределения вероятностей представлен на рис. 6 График
- 35. Числовые характеристики случайных величин Закон распределения полностью характеризует случайную величину.
- 36. Математическое ожидание дискретной случайной величины X – это сумма произведений всех
- 37. Математическое ожидание случайной величины (как дискретной, так и непрерывной) есть неслучайная
- 38. Дисперсия и среднее квадратичное отклонение – это числовые характеристики случайной величины,
- 39. Дисперсией (рассеянием) случайной величины (как дискретной, так и непрерывной) называют математическое
- 40. «Нормальный закон распределения вероятностей непрерывной случайной величины» Закон нормального распределения вероятностей
- 41. К случайным явлениям, подчиняющимся нормальному закону распределения, относятся ошибки измерений производственных
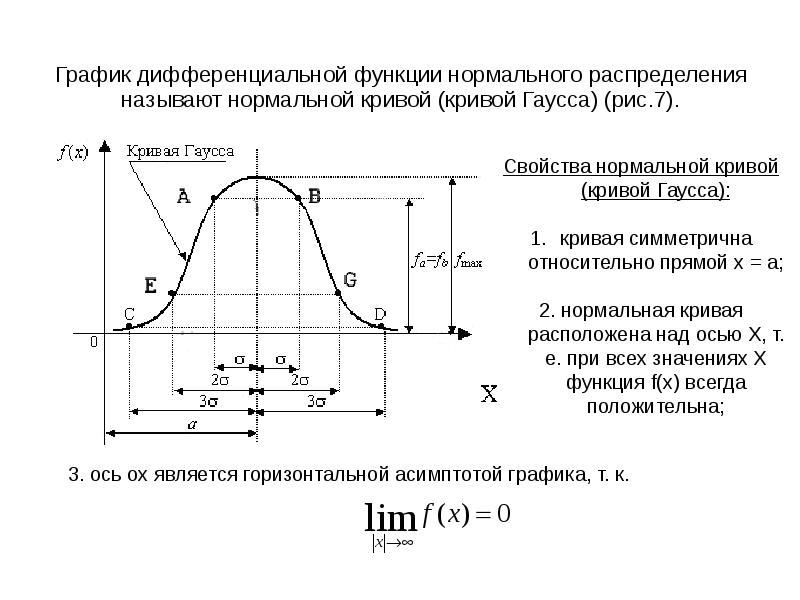
- 42. График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса) (рис.7).
- 43. 4. при x = a функция f(x) имеет максимум равный
- 44. в точках E и G, при
- 45. Асимптотически приближаясь к оси абсцисс, кривая Гаусса в точках C и
- 46. Если случайная величина распределена нормально, то абсолютная величина ее отклонения от
- 47. При a=0 нормальная кривая симметрична относительно оси ординат. При a=0 нормальная
- 48. При этом, при любых значениях и площадь ограниченная нормальной
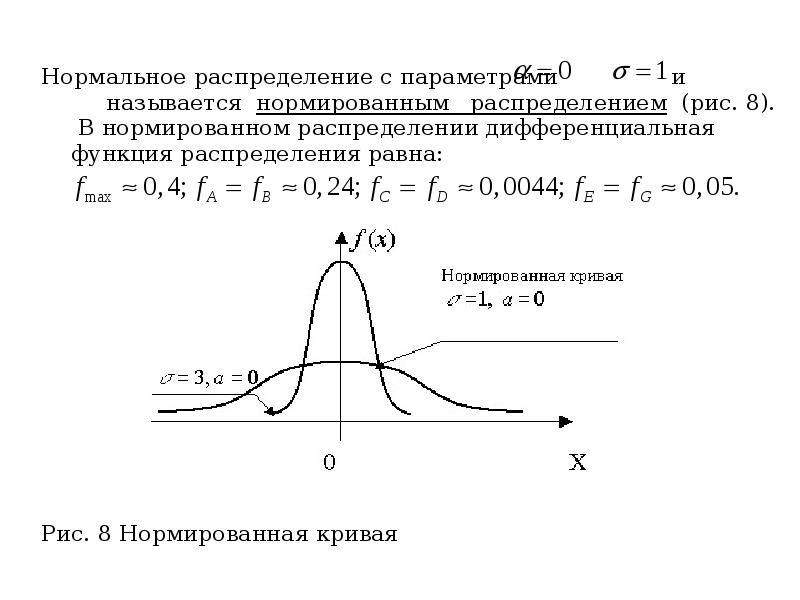
- 49. Нормальное распределение с параметрами и
- 50. Интегральная функция общего нормального распределения имеет вид: Интегральная функция общего нормального
- 51. Пусть случайная величина X распределена по нормальному закону в интервале (c,
- 52. Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и
- 53. Скачать презентацию













































Слайды и текст этой презентации
Похожие презентации





























