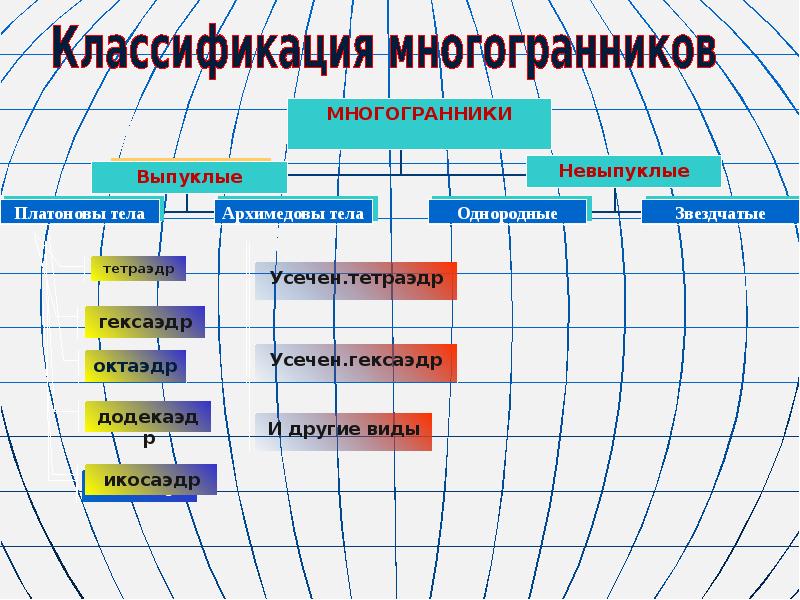
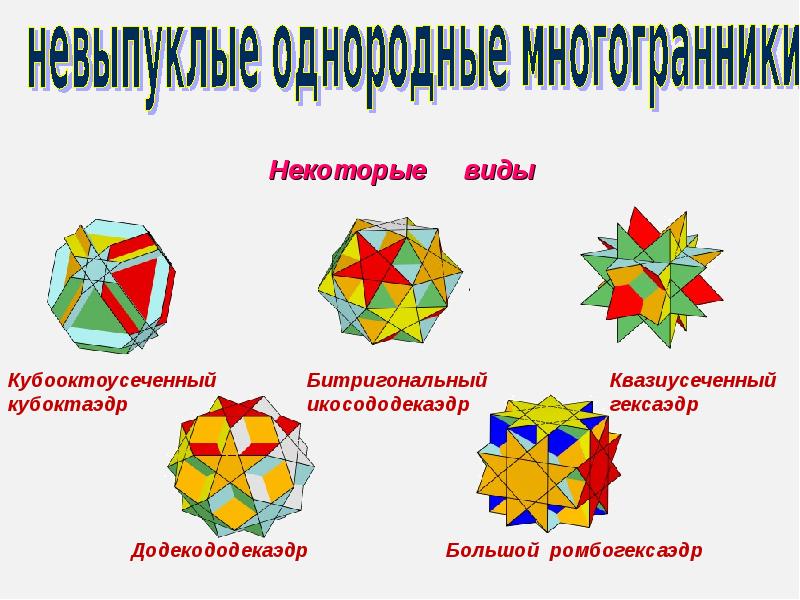
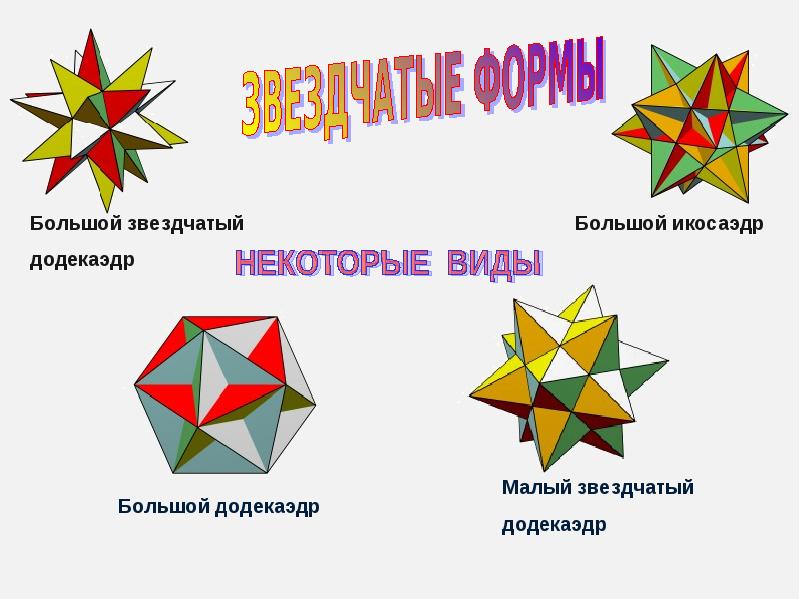
Презентация, доклад Классификация многогранников

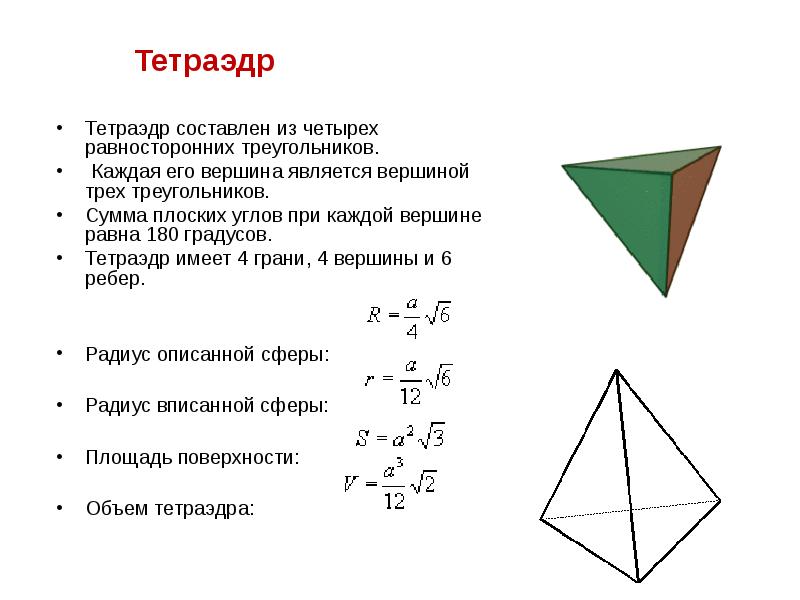
Тетраэдр

Куб (гексаэдр)

Октаэдр

Додекаэдр

Икосаэдр

Леонардо да Винчи любил делать из дерева каркасные модели многогранников. Когда его друг Пачоли издал в 1509 году в Венеции книгу «О божественной пропорции», иллюстрациями к ней послужили 59 рисунков, сделанных Леонардо со своих моделей.

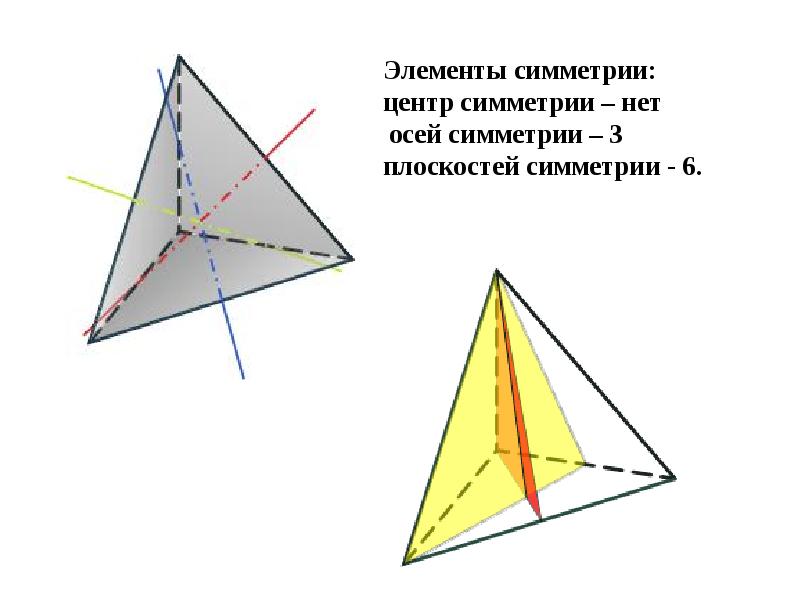
Тетраэдр Тетраэдр Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Радиус описанной сферы: Радиус вписанной сферы: Площадь поверхности: Объем тетраэдра:

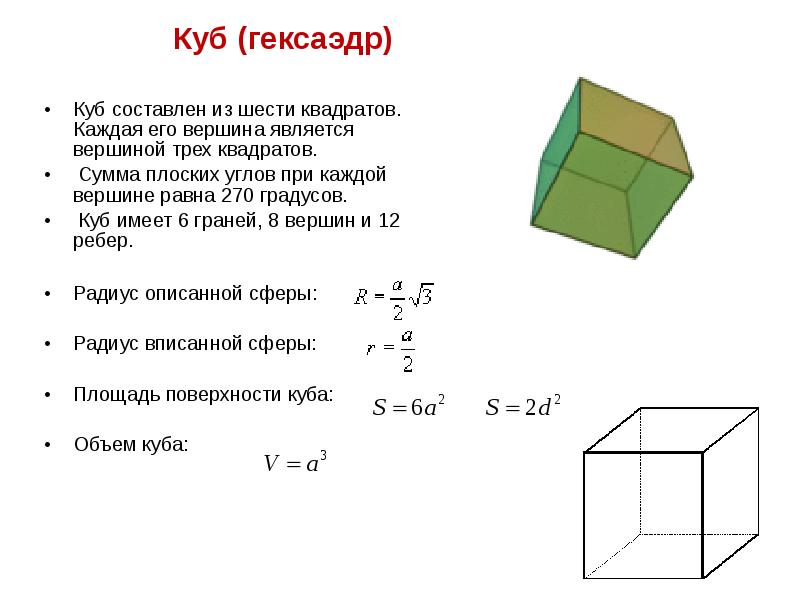
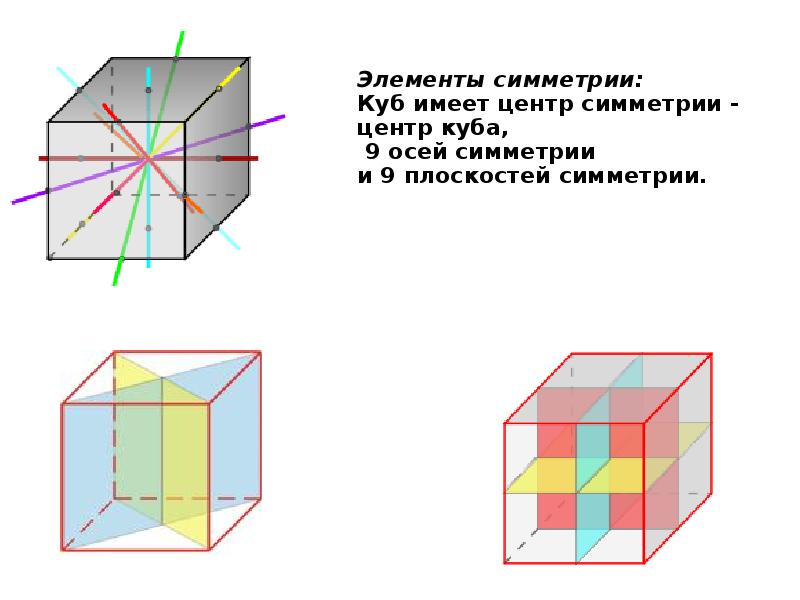
Куб (гексаэдр) Куб (гексаэдр) Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270 градусов. Куб имеет 6 граней, 8 вершин и 12 ребер. Радиус описанной сферы: Радиус вписанной сферы: Площадь поверхности куба: Объем куба:

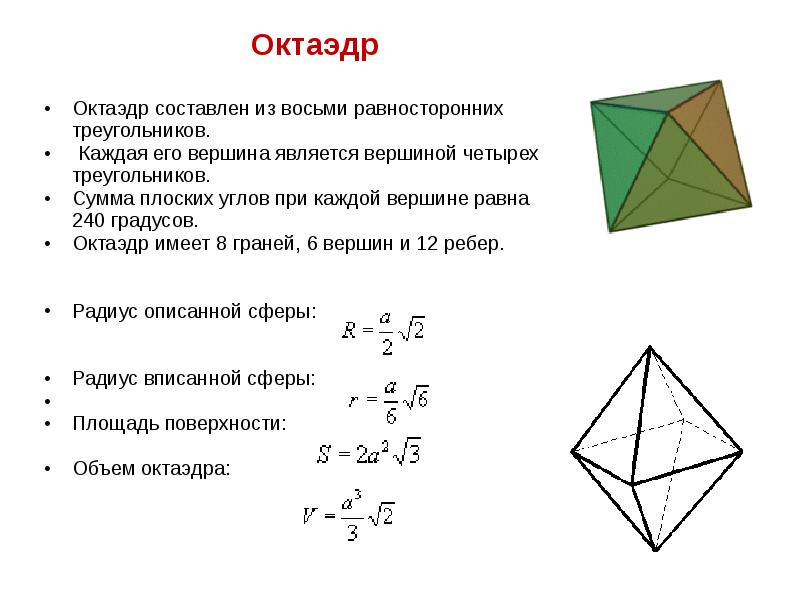
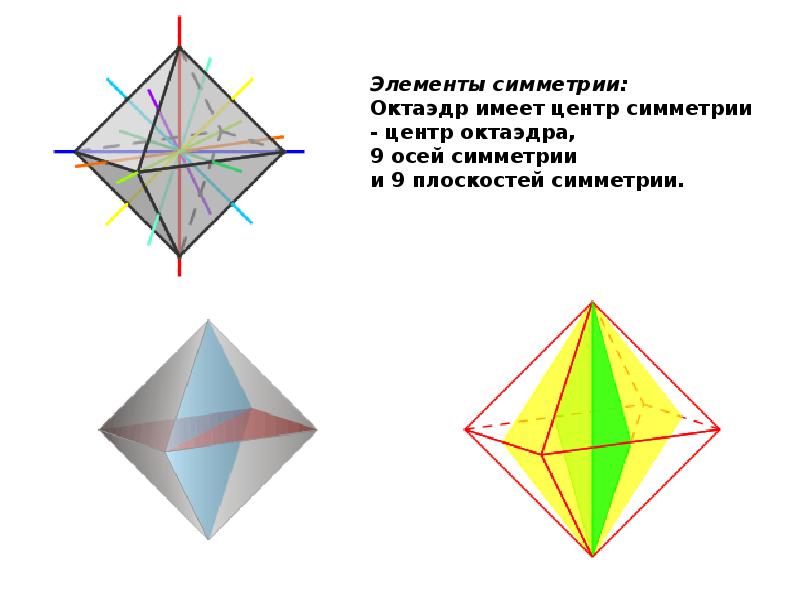
Октаэдр Октаэдр Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна 240 градусов. Октаэдр имеет 8 граней, 6 вершин и 12 ребер. Радиус описанной сферы: Радиус вписанной сферы: Площадь поверхности: Объем октаэдра:

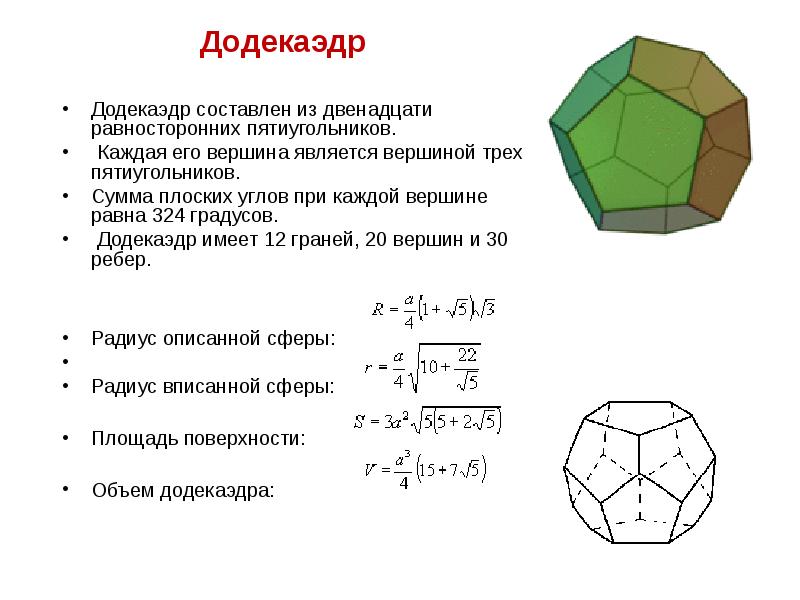
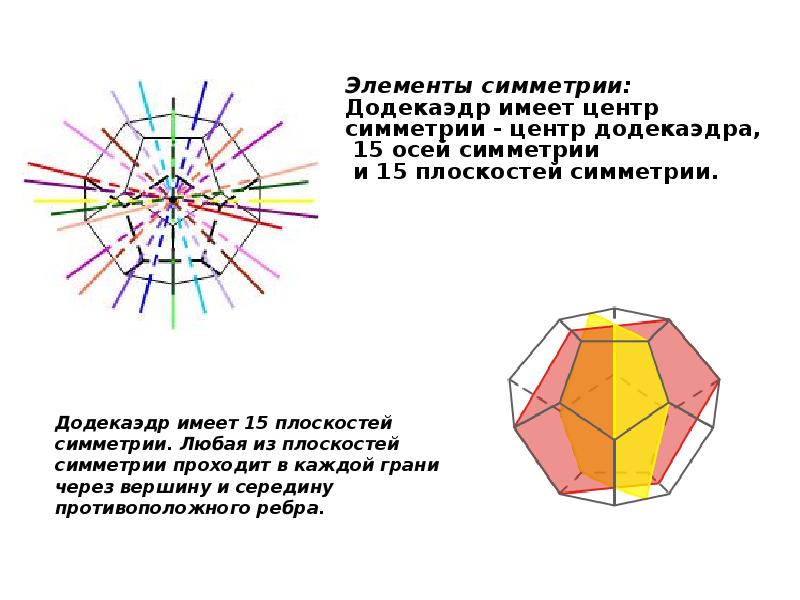
Додекаэдр Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324 градусов. Додекаэдр имеет 12 граней, 20 вершин и 30 ребер. Радиус описанной сферы: Радиус вписанной сферы: Площадь поверхности: Объем додекаэдра:

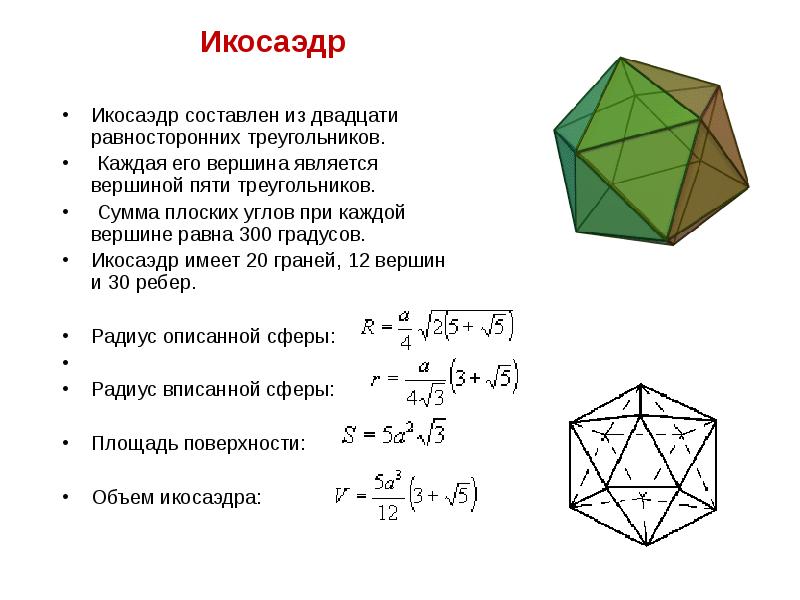
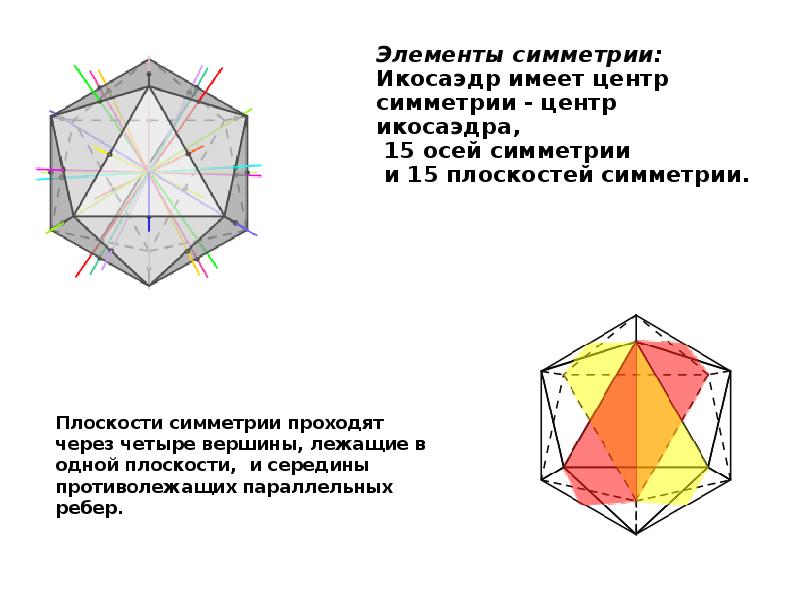
Икосаэдр Икосаэдр Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300 градусов. Икосаэдр имеет 20 граней, 12 вершин и 30 ребер. Радиус описанной сферы: Радиус вписанной сферы: Площадь поверхности: Объем икосаэдра:

Правильные многогранники существовали на Земле задолго до появления на ней человека- кубы поваренной соли, тетраэдры сурьмянистого сернокислого натрия, октаэдры хромовых квасцов, икосаэдры бора и додекаэдры радиолярий , микроскопических морских организмов…

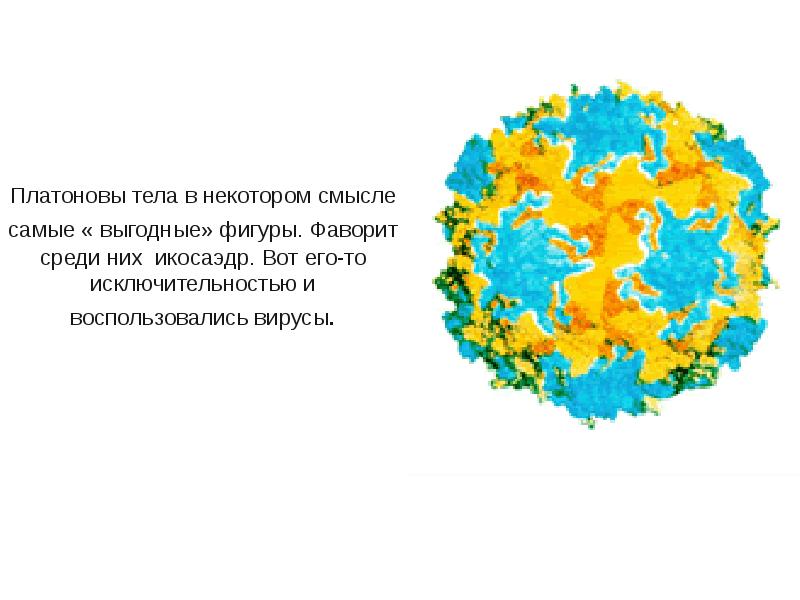
Платоновы тела в некотором смысле самые « выгодные» фигуры. Фаворит среди них икосаэдр. Вот его-то исключительностью и воспользовались вирусы.

На гравюре "Четыре тела" (Эшер) изображено пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

ДРУГОЙ МИР

Если вы услышите, что кто-то не любит математику, не верьте. Её нельзя не любить- она и вовне, и внутри нас. Её можно только знать или не знать.

«В огромном саду геометрии каждый найдёт букет себе по вкусу». Давид Гильберт.