Конические поверхности. Поверхности вращения презентация

Конические поверхности. Поверхности вращения.

Конические поверхности Конической поверхностью называется поверхность, образованная прямыми — образующими конуса, — проходящими через данную точку — вершину конуса — и пересекающими данную линию — направляющую конуса.

Пусть направляющая конуса задана уравнениями: Пусть направляющая конуса задана уравнениями: а вершина S конуса имеет координаты x0, y0, z0. Уравнения образующей запишем как уравнения прямой, проходящей через две точки S(x0, y0, z0) и M(x, y, z), принадлежащие направляющей (60): где X ,Y, Z - текущие координаты точек образующих. Исключая из уравнений (60) и (61) x, y, z, получим уравнение относительно переменных X, Y, Z, т.е. уравнение конической поверхности.

Поверхности вращения Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i (рис.96). Геометрическая часть определителя состоит из двух линий: образующей m и оси i

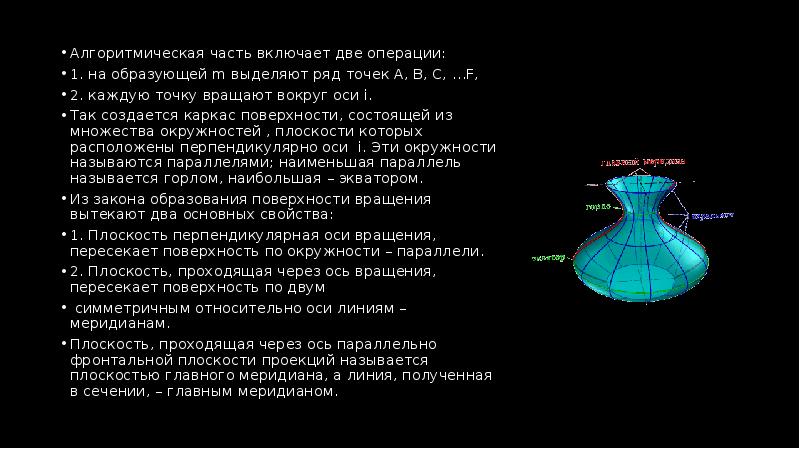
Алгоритмическая часть включает две операции: Алгоритмическая часть включает две операции: 1. на образующей m выделяют ряд точек A, B, C, …F, 2. каждую точку вращают вокруг оси i. Так создается каркас поверхности, состоящей из множества окружностей , плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором. Из закона образования поверхности вращения вытекают два основных свойства: 1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели. 2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам. Плоскость, проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.

Для вывода уравнения поверхности вращения необходимо выбрать систему координат. Чтобы уравнение поверхности вращения выглядело проще, ось вращения принимают за одну из координатных осей. Для вывода уравнения поверхности вращения необходимо выбрать систему координат. Чтобы уравнение поверхности вращения выглядело проще, ось вращения принимают за одну из координатных осей. Пусть в координатной плоскости Oyz задана кривая L уравнением F(Y, Z)=0 Вращаем кривую L вокруг оси Oy. Получим некоторую поверхность. Пусть M(x, y, z) - произвольная точка получившейся поверхности.

Уравнение и есть искомое уравнение поверхности вращения. Таким образом, чтобы получить уравнение поверхности, образованной вращением линии L, лежащей в плоскости Oyz, вокруг оси Oy, нужно в уравнении этой линии заменить z на Аналогичные правила будут иметь место и по отношению к уравнениям поверхностей, полученных вращением плоских линий вокруг других координатных осей.

Источники информации: http://graph.power.nstu.ru/wolchin/umm/Graphbook/book/001/038/01.htm http://vm.psati.ru/online-math-sem-1/page-2-10-01.html

Над презентацией работали: Соломатова Дарья Боргоякова Кристина Плаксин Никита Шурко Андрей Турков Виталий Назмутдинов Кирилл

Спасибо за внимание!