Л. Эйлер и развитие математического анализа в XVIII веке презентация

Л. ЭЙЛЕР И РАЗВИТИЕ МАТЕМАТИЧЕСКОГО АНАЛИЗА В XVIII ВЕКЕ Студента очной формы обучения Направления подготовки 01.03.02 Прикладная математика и информатика 1 курса группы 92061605 Гончарова Дмитрия Викторовича

План Введение Понятие математического анализа Вклад Л.Эйлера в развитие математического анализа Заключение

Введение Леонард Эйлер - самый продуктивный математик в истории, автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. Многие его работы оказали значительное влияние на развитие науки.

Понятие математического анализа Математический анализ - совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление.

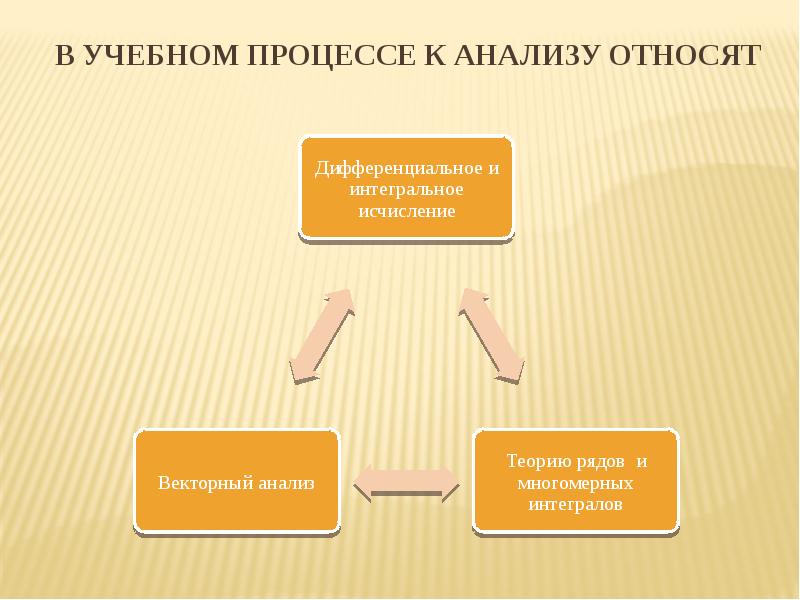
В учебном процессе к анализу относят

Предшественниками математического анализа были античный метод исчерпывания и метод неделимых. Все три направления, включая анализ, роднит общая исходная идея: разложение на бесконечно малые элементы, природа которых, впрочем, представлялась авторам идеи довольно туманно.

Вклад Л.Эйлера в развитие математического анализа Научное наследие Леонарда Эйлера колоссально. Ему принадлежат классические результаты в математическом анализе. Он продвинул его обоснование, существенно развил интегральное исчисление, методы интегрирования обыкновенных дифференциальных уравнений и уравнений в частных производных. Эйлеру принадлежит знаменитый шеститомный курс математического анализа, включающий «Введение в анализ бесконечно малых», «Дифференциальное исчисление» и «Интегральное исчисление». На этой «аналитической трилогии» учились многие поколения математиков всего мира.

Вклад Л.Эйлера в развитие математического анализа Эйлер получил основные уравнения вариационного исчисления и определил пути дальнейшего его развития, подведя главные итоги своих исследований в этой области в монографии «Метод нахождения кривых линий, обладающих свойствами максимума или минимума».

Вклад Л.Эйлера в развитие математического анализа Одна из главных заслуг Эйлера перед наукой — монография «Введение в анализ бесконечно малых» (1748). В 1755 году вышло дополненное «Дифференциальное исчисление», а в 1768—1770 годах — три тома «Интегрального исчисления». В совокупности это фундаментальный, хорошо иллюстрированный примерами курс, с продуманной терминологией и символикой. «Можно с уверенностью сказать, что добрая половина того, что преподаётся теперь в курсах высшей алгебры и высшего анализа, находится в трудах Эйлера» (Н. Н. Лузин).

Вклад Л.Эйлера в развитие математического анализа Перемены в математическом анализе отражены в обширном трактате Эйлера. Изложение анализа открывает двухтомное «Введение», где собраны изыскания о различных представлениях элементарных функций. Термин «функция» впервые появляется лишь в 1692 у Лейбница, однако на первые роли его выдвинул именно Эйлер. Изначальная трактовка понятия функции состояла в том, что функция — это выражение для счёта или аналитическое выражение.

Вклад Л.Эйлера в развитие математического анализа В отличие от Лопиталя Эйлер подробно рассматривает трансцендентные функции и в особенности два наиболее изученные их классы — показательные и тригонометрические. Он обнаруживает, что все элементарные функции могут быть выражены при помощи арифметических действий и двух операций — взятия логарифма и экспоненты.

Вклад Л.Эйлера в развитие математического анализа Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее: а отсюда . Полагая и , он получает отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

Заключение Большой вклад в развитие математического анализа внес Л.Эйлер. Он принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику по руководствам, первыми образцами которых явились классические монографии Эйлера. Он был прежде всего математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный.