Математическая статистика (лекция 6) презентация

Математические методы в биологии Блок 3. Математическая статистика Лекция 6

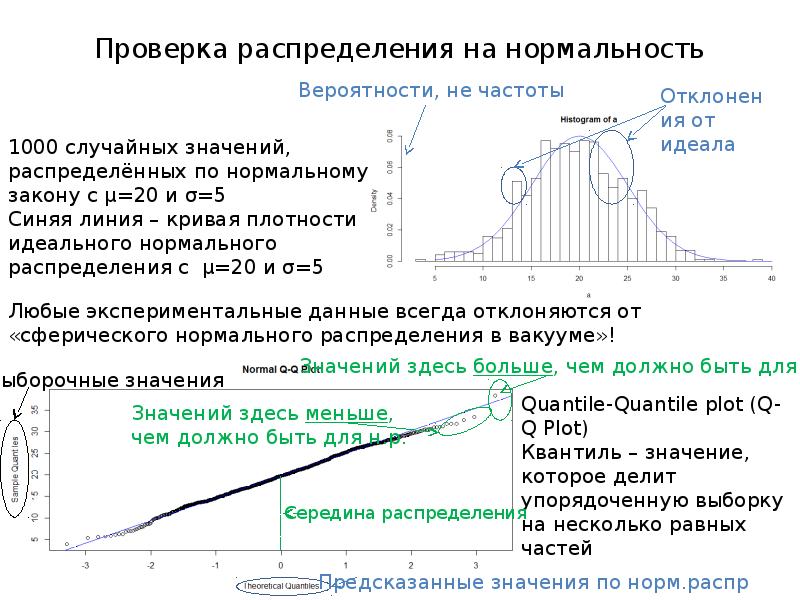
Проверка распределения на нормальность

Формальные тесты на нормальность Визуализация (гистограмма или Q-Q plot) позволяют определить, в каких конкретно точках выборочные значения отклоняются от нормального распределения. При этом Q-Q plot предпочтительней, когда наблюдений мало. Формальные тесты отвечают на вопрос, нормально ли распределение в принципе. Тест Шапиро-Уилкса H0: выборка распределена по нормальному закону () H1: выборка распределена по нормальному закону () Если p-value>0,05 – распределение соответствует нормальному закону () Тест Колмогорова-Смирнова H0: случайная величина X (значения признака в выборке) имеет распределение F(X) (нормальное распределение – частный случай) H1: её распределение отличается от F(X) => Если p-value>0,05 – случайная величина имеет распределение F(X)

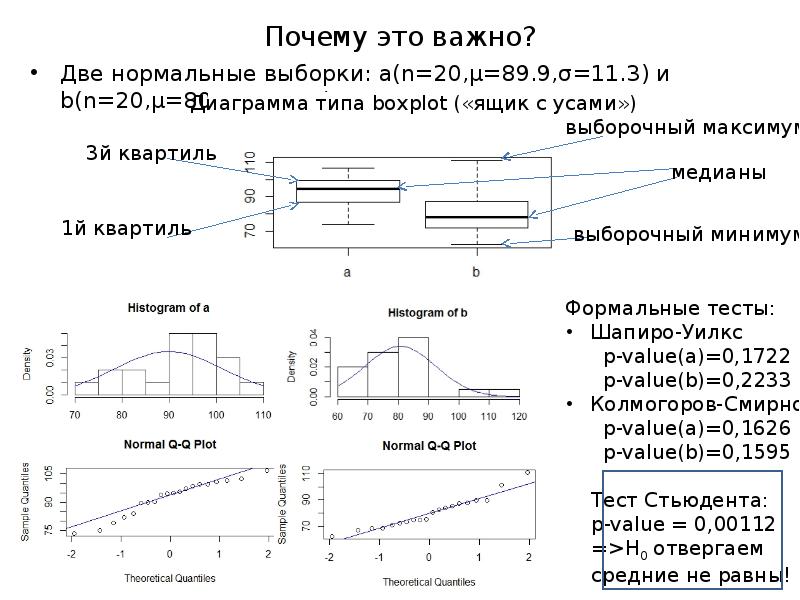
Почему это важно? Две нормальные выборки: a(n=20,μ=89.9,σ=11.3) и b(n=20,μ=80.7,σ=11.7)

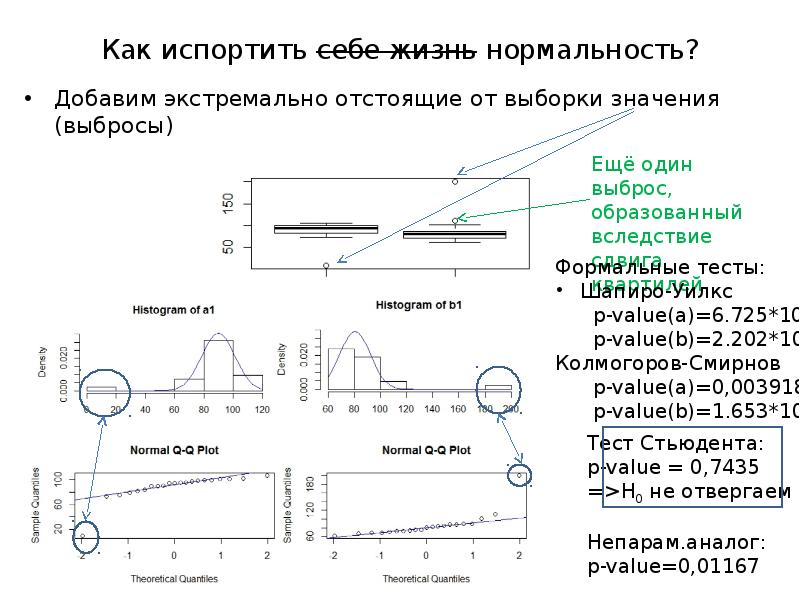
Как испортить себе жизнь нормальность? Добавим экстремально отстоящие от выборки значения (выбросы)

Однофакторный дисперсионный анализ Сравниваем между собой не две, а несколько групп Пример. Длина лепестка у ирисов трёх сортов Наблюдения делятся на группы по факторному (номинативному) признаку, выраженному независимой переменной Пример. Все собранные ирисы делятся на три группы – сорт Versicolor, сорт Virginica и сорт Setosa. Переменная «сорт ириса» – независимая переменная. Изучаем зависимую переменную – количественную переменную, выраженность которой зависит от независимой. Пример. Зависимая переменная – длина лепестка ириса.

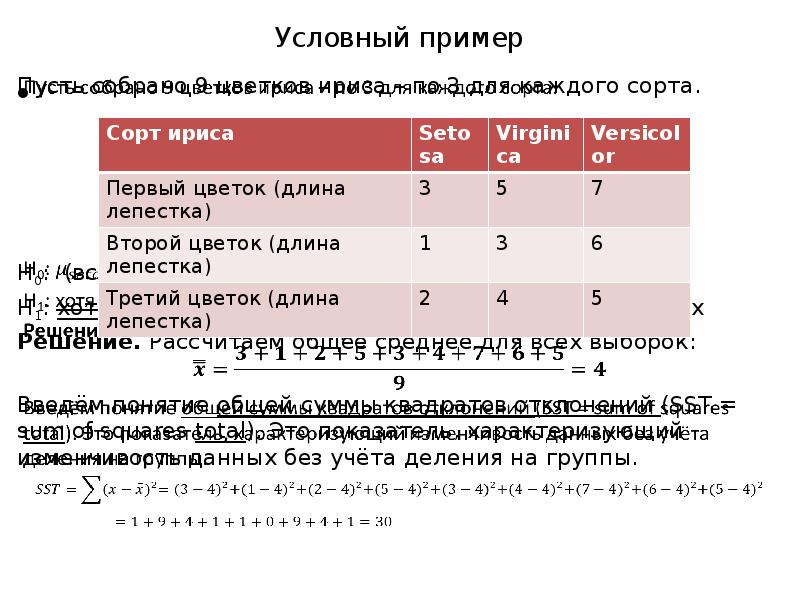
Условный пример Пусть собрано 9 цветков ириса – по 3 для каждого сорта. H0: (все выборки – из одной ГС) H1: хотя бы одно истинное среднее отлично от остальных Решение. Рассчитаем общее среднее для всех выборок: Введём понятие общей суммы квадратов отклонений (SST = sum of squares total). Это показатель, характеризующий изменчивость данных без учёта деления на группы.

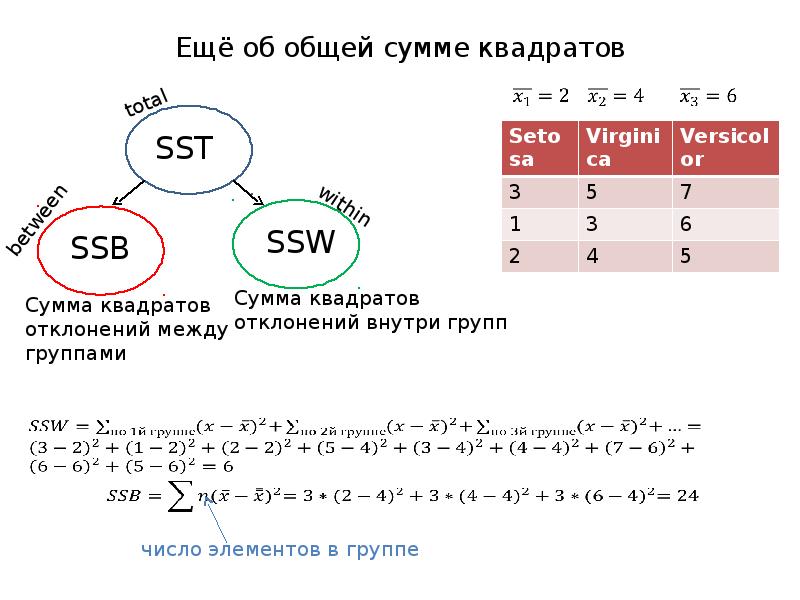
Ещё об общей сумме квадратов

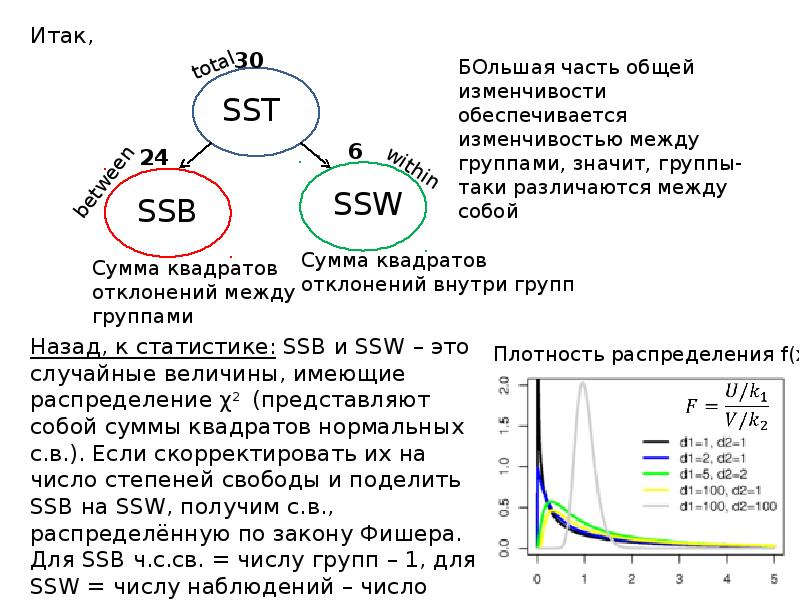
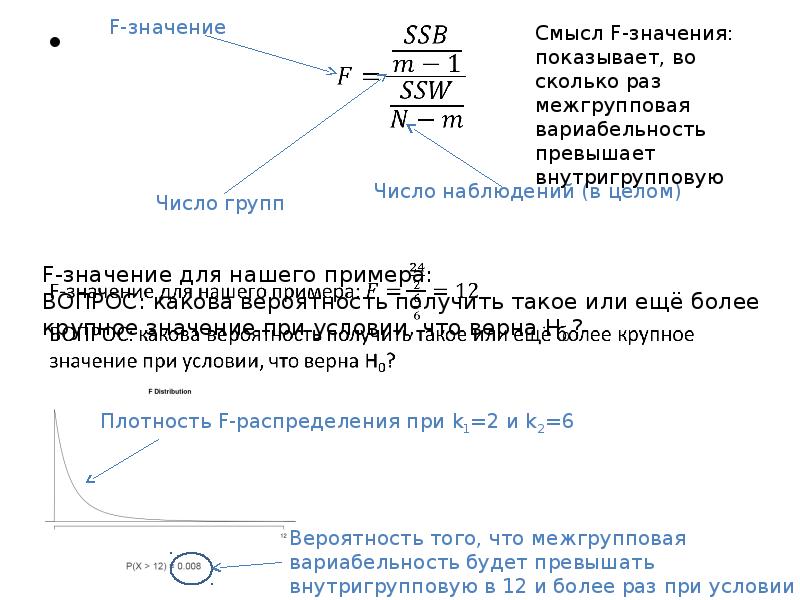
Итак, Итак, Назад, к статистике: SSB и SSW – это случайные величины, имеющие распределение χ2 (представляют собой суммы квадратов нормальных с.в.). Если скорректировать их на число степеней свободы и поделить SSB на SSW, получим с.в., распределённую по закону Фишера. Для SSB ч.с.св. = числу групп – 1, для SSW = числу наблюдений – число групп.

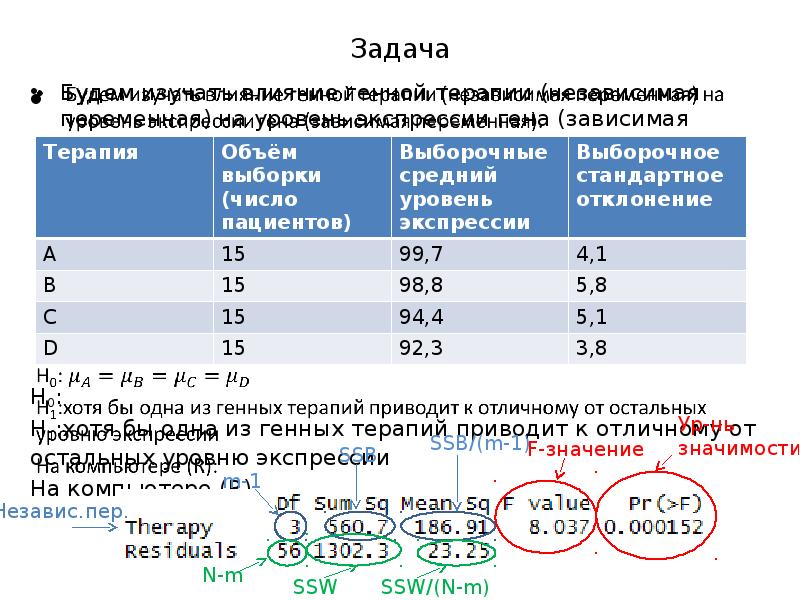
Задача Будем изучать влияние генной терапии (независимая переменная) на уровень экспрессии гена (зависимая переменная). H0: H1:хотя бы одна из генных терапий приводит к отличному от остальных уровню экспрессии На компьютере (R):

Множественные сравнения ВОПРОС: Можем ли мы теперь сказать, какая конкретно пара терапий статистически значимо различается между собой по уровню экспрессии гена? ВСПОМНИМ КОМБИНАТОРИКУ И ТЕРВЕР. Сколько попарных сравнений надо выполнить, чтобы перебрать все возможные пары A,B,C,D? Пусть пороговое значение отвержения H0 = 0,05, т.е. вероятность совершить ошибку 1го рода для каждого из 6 тестов равна 0,05. Какова вероятность того, что хотя бы в одном из 6 тестов будет совершена ошибка первого рода (H0 будет отклонена неправомерно, а различия между средними на самом деле случайны)? Вероятность не-совершения ошибки = 0,95. (вероятность того, что не будет совершена ошибка в 6 тестах), значит, вероятность того, что хотя бы в одном из тестов она будет совершена, = 1-0,735=0,265. Вывод. Даже если различий между средними на самом деле нет, в 26,5% случаев при извлечении 4х выборок из одной ГС между какими-то из них мы будем получать статистически значимые различия!

Что же делать? Поправка на множественное сравнение Бонферрони. Идея. Вероятность совершения ошибки первого рода растёт пропорционально увеличению числа попарных сравнений. Почему бы не уравновесить этот рост с помощью корректировки критического p-value в сторону убывания? А именно, разделим критическое значение p-value на число попарных сравнений: 0,05/6=0,008333. Тогда вероятность того, что в 6ти тестах будет совершена хотя бы одна ошибка 1го рода = 1-(1-0,008333)6 =0,049. НО! Сильное снижение критического уровня p-value ведёт к увеличению вероятности совершить ошибку 2го рода (H0 не отвергается, хотя должна была бы). Альтернатива – использование критерия Тьюки (критерий достоверно значимой разности Тьюки,  Tukey's honestly significant difference test, Tukey's HSD test) - похож на критерий Стьюдента, но стандартная ошибка среднего рассчитывается по-другому

Критерий Тьюки Пусть есть m групп: A,B,C,… H0, H1 Для каждого из попарных сравнений рассчитывается величина: Если число наблюдений в A и B разное, то В нашем примере

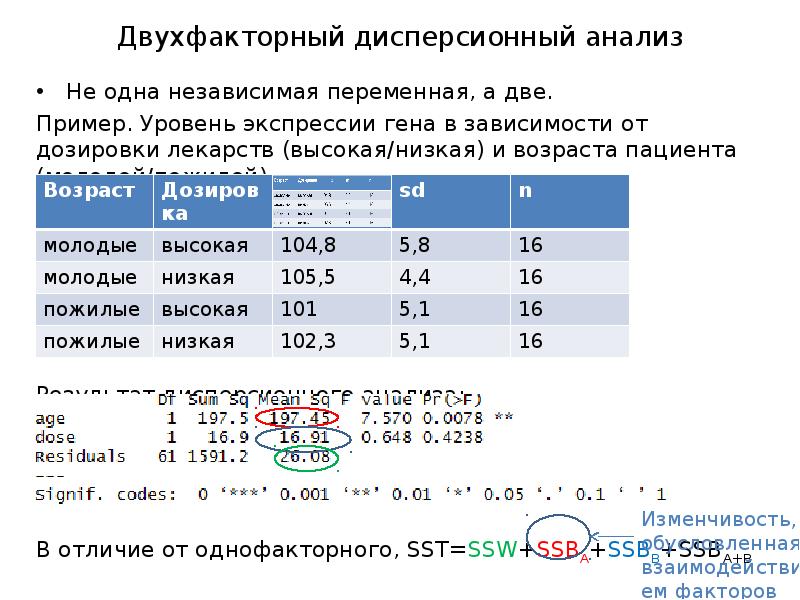
Двухфакторный дисперсионный анализ Не одна независимая переменная, а две. Пример. Уровень экспрессии гена в зависимости от дозировки лекарств (высокая/низкая) и возраста пациента (молодой/пожилой). Результат дисперсионного анализа: В отличие от однофакторного, SST=SSW+SSBA+SSBB+SSBA+B

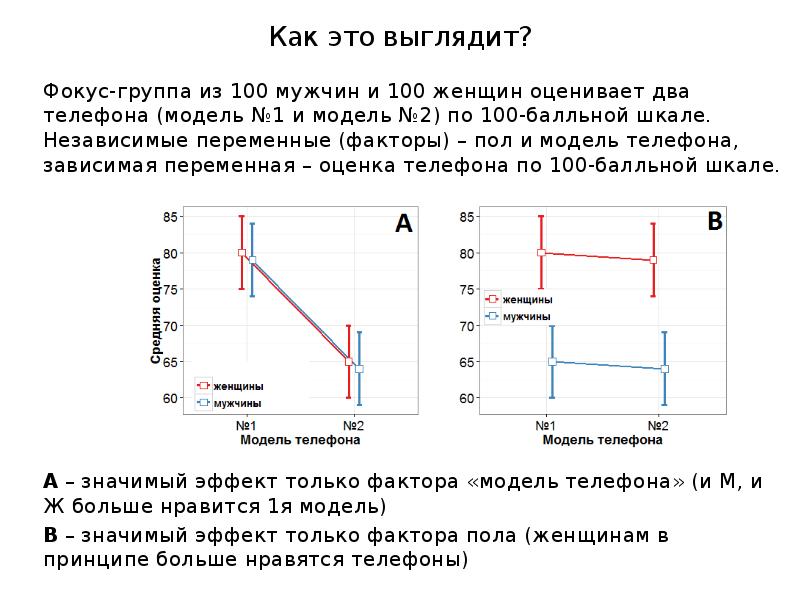
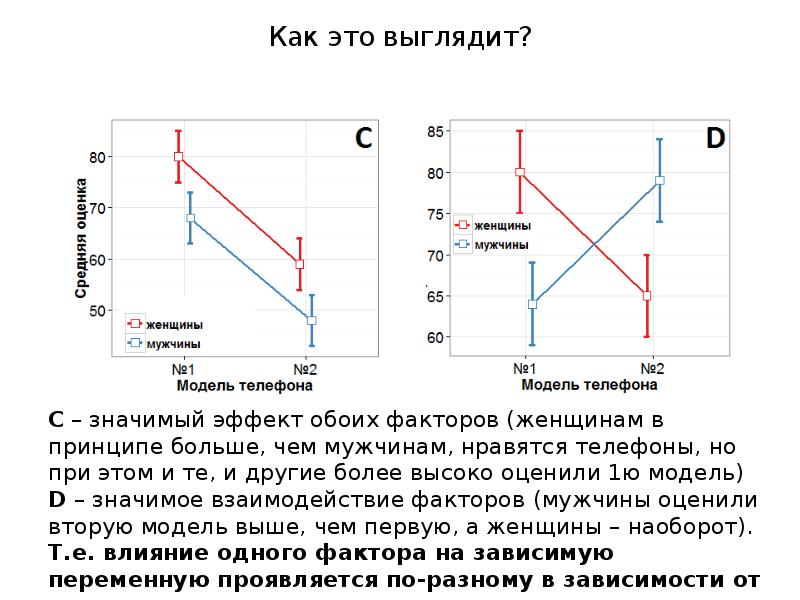
Как это выглядит? Фокус-группа из 100 мужчин и 100 женщин оценивает два телефона (модель №1 и модель №2) по 100-балльной шкале. Независимые переменные (факторы) – пол и модель телефона, зависимая переменная – оценка телефона по 100-балльной шкале. A – значимый эффект только фактора «модель телефона» (и М, и Ж больше нравится 1я модель) B – значимый эффект только фактора пола (женщинам в принципе больше нравятся телефоны)

Требования к использованию дисперсионного анализа Нормальность распределения зависимой переменной в каждой из групп Гомогенность дисперсий (дисперсии признака внутри групп равны между собой) Могут нарушаться при большом объёме выборок (>50). Нормальность распределения проверяется: Графически (гистограмма плотности вероятностей, qq-plot) Формальными тестами (Шапиро-Уилкса, Колмогорова-Смирнова) Гомогенность дисперсий проверяется: Графически (боксплот) Формальными тестами (тест Левена, при p>0,05 дисперсии одинаковы)

Резюме по сравнению средних Для сравнения средних значений в двух группах – t-test Для сравнения средних в трёх и более группах – дисперсионный анализ Если результаты дисперсионного анализа говорят, что по крайней мере в двух группах средние различны, – использовать критерий Тьюки

Домашнее задание Посмотреть научно-популярный доклад «Статистика и плохая наука: как поправка на множественные сравнения объясняет парадоксальные результаты исследований» Ссылка: https://www.youtube.com/watch?v=dcVG0NtZMwE