Матрицы презентация
Содержание
- 2. М А Т Р И Ц Ы 1.ОПРЕДЕЛЕНИЯ О п
- 3. М А Т Р И Ц Ы 1.ОПРЕДЕЛЕНИЯ Матрицу
- 4. М А Т Р И Ц Ы 1.ОПРЕДЕЛЕНИЯ О
- 5. М А Т Р И Ц Ы 1.ОПРЕДЕЛЕНИЯ З
- 6. М А Т Р И Ц Ы 1.ОПРЕДЕЛЕНИЯ Квадратной
- 7. М А Т Р И Ц Ы 1.ОПРЕДЕЛЕНИЯ О
- 8. М А Т Р И Ц Ы 1.ОПРЕДЕЛЕНИЯ О
- 9. М А Т Р И Ц Ы 2.ОПЕРАЦИИ НАД МАТРИЦАМИ О
- 10. М А Т Р И Ц Ы 2.ОПЕРАЦИИ НАД МАТРИЦАМИ 1)
- 11. М А Т Р И Ц Ы 2.ОПЕРАЦИИ НАД МАТРИЦАМИ Свойства
- 12. М А Т Р И Ц Ы 2.ОПЕРАЦИИ НАД МАТРИЦАМИ 2)
- 13. М А Т Р И Ц Ы 2.ОПЕРАЦИИ НАД МАТРИЦАМИ Свойства
- 14. М А Т Р И Ц Ы 2.ОПЕРАЦИИ НАД МАТРИЦАМИ 3)
- 15. М А Т Р И Ц Ы 3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
- 16. М А Т Р И Ц Ы 3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
- 17. М А Т Р И Ц Ы 3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
- 18. М А Т Р И Ц Ы 3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
- 19. М А Т Р И Ц Ы 4. РАНГ МАТРИЦЫ О
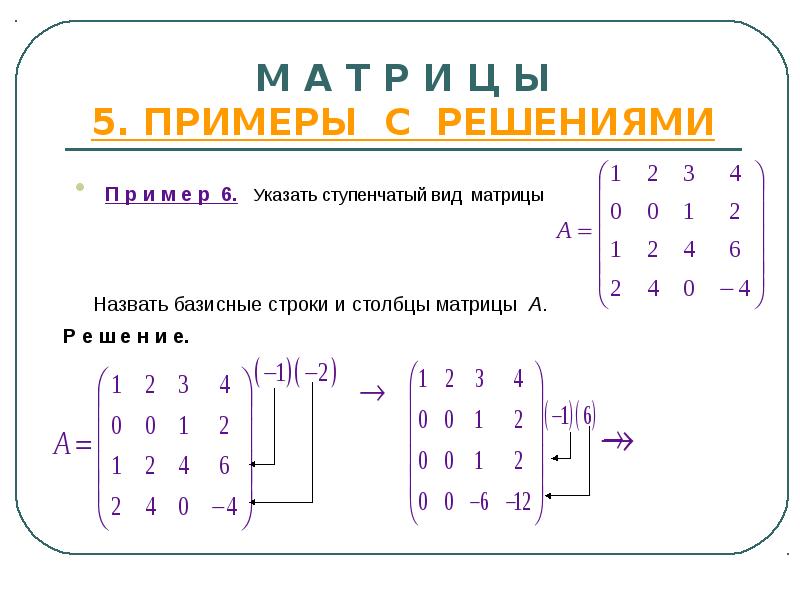
- 20. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
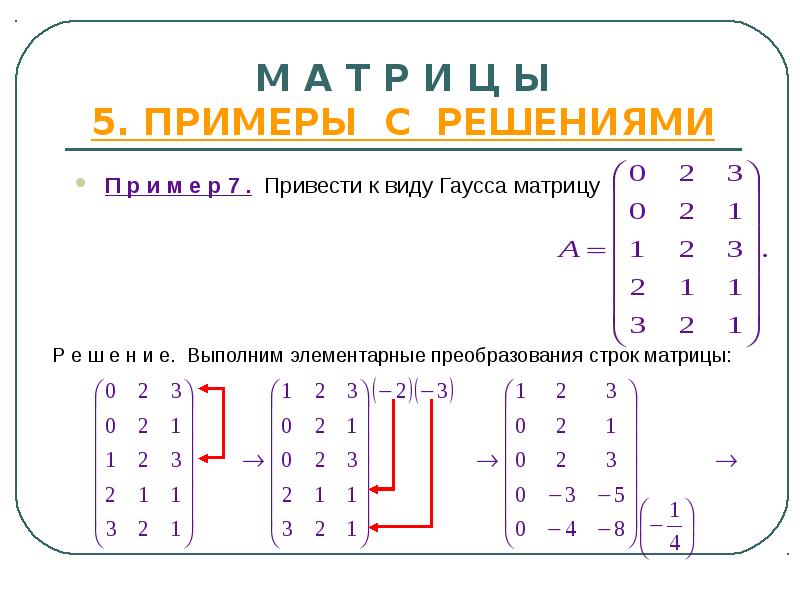
- 21. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
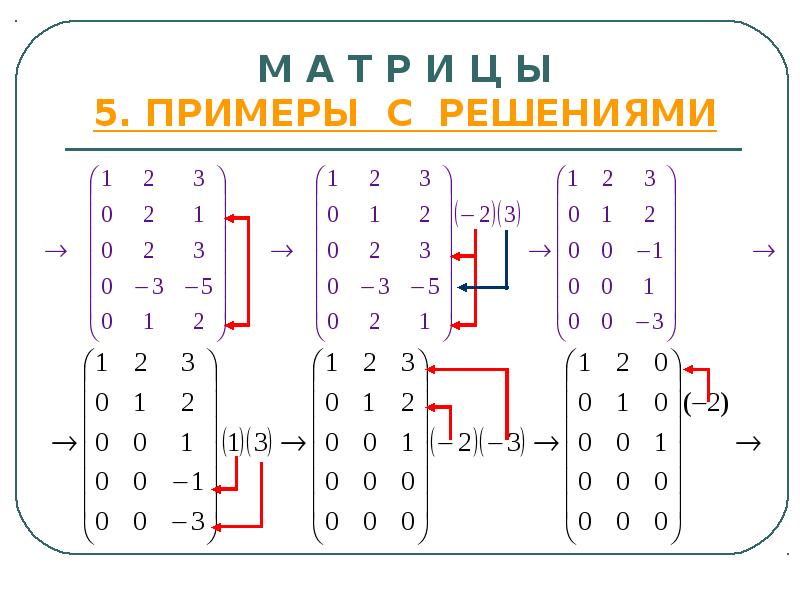
- 22. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
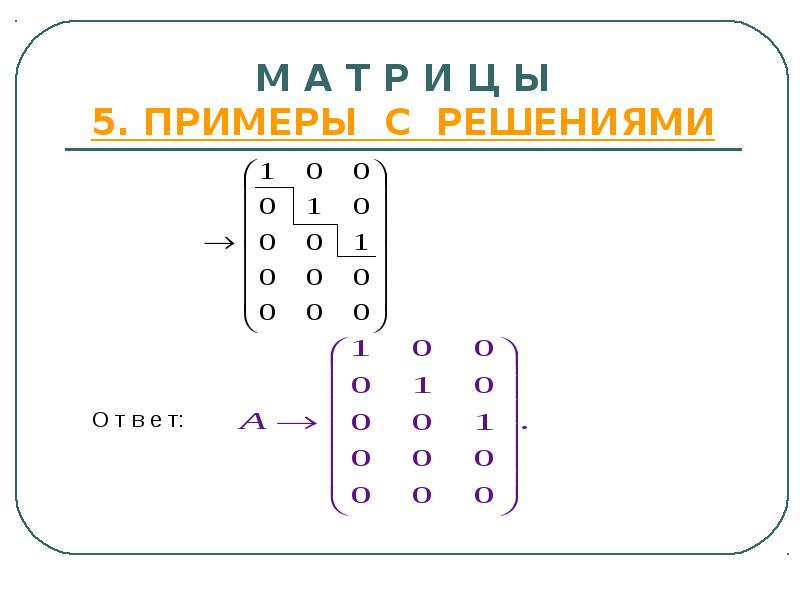
- 23. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
- 24. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
- 25. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
- 26. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
- 27. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
- 28. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
- 29. М А Т Р И Ц Ы 5. ПРИМЕРЫ С РЕШЕНИЯМИ
- 30. Скачать презентацию

























Слайды и текст этой презентации
Похожие презентации





























