Модели стационарных рядов. АРСС-модели презентация

МОДЕЛИ СТАЦИОНАРНЫХ РЯДОВ АРСС -модели

Стационарные ряды Аддитивная модель тренда временного ряда Модель, адекватно описывающую поведение случайных остатков , строят в классе стационарных рядов Стационарность временного ряда связывают с требованием, чтобы он имел постоянное среднее и колебался вокруг этого среднего с постоянной дисперсией. На практике, моделируют случайные остатки, которые получаются после элиминирования из исходного временного ряда его тенденции остатки, невязки;

Основные характеристики стационарных рядов Модель: (либо исходный ряд, например, урожайность ячменя; либо после удаления тенденции) - оценка среднего значения - оценка дисперсии - оценка автоковариационной функции порядка - оценка автокорреляционной функции порядка

Тестирование стационарности - постоянство математического ожидания Параметрические тесты Стьюдента и Фишера; Непараметрический тест Манна-Уитни – постоянство дисперсии Параметрические тесты Фишера, Кокрена и Бартлета; Непараметрический тест Сиджела-Тьюки или - постоянство автоковариационной или автокорреляционной функций Для проверки гипотез могут применяться те же критерии, что и для средних (автокорреляции) или дисперсий (автоковариации)

Операторы B – оператор сдвига назад: – оператор разности: – оператор суммирования: – белый шум с дисперсией   Модель основывается на гипотезе, что изучаемый процесс является выходом линейного фильтра, на вход которого подан процесс белого шума:

Типы моделей Если последовательность конечна или бесконечна, но сходится, то фильтр называется устойчивым, а процесс будет стационарным. Тогда — среднее значение, вокруг которого процесс варьирует. В противном случае — нестационарен и не имеет особого смысла, кроме как некой точки отсчета уровня процесса. Рассмотрим некоторые специфические модели, получаемые линейной фильтрацией белого шум: модель авторегрессии (АР), модель скользящего среднего (СС) и смешанную модель (АРСС). Некоторые нестационарные процессы описываются моделью авторегрессии проинтегрированного скользящего среднего (АРПСС). При дальнейшем рассмотрении будем считать =0.

Авторегрессионная модель (АР) Текущее значение процесса выражается через конечную линейную совокупность предыдущих значений процесса и возмущения - авторегрессионный процесс порядка р, который обозначают АР(р) В этой модели р + 2 неизвестных параметра , , и , которые должны быть оценены по имеющимся данным об изучаемом процессе Процессы могут быть стационарными и нестационарными. Для решения практических задач, как правило, достаточно р≤ 2.

Модель скользящего среднего (СС) В модели конечного скользящего среднего текущее значение процесса линейно зависит от конечного числа предыдущих значений белого шума Это процесс скользящего среднего порядка q или кратко СС (q). Следует отметить, что в данном случае название ≪скользящее среднее≫ вводит в заблуждение, так как веса не обязательно должны в сумме давать единицу и не обязательно должны быть положительными. Если введем оператор процесса скользящего среднего порядка q , то модель СС (q) может быть записана кратко: Она содержит q + 2 неизвестных параметра . Обычно q = 0, 1, 2

Двойственность в представлении АР и СС Если в модели АР(р) последовательно выразить , выразить через , , , … , то получим эквивалентную запись через бесконечную взвешенную сумму реализаций белого шума: Однако здесь количество неизвестных параметров модели оказывается бесконечным и форма АР(р) явно предпочтительней. Аналогично, модель СС(q) можно представить через АР бесконечного порядка. Т.е. АР и СС являются эквивалентными формами записи общего линейного процесса.

Смешанная модель (АРСС) В некоторых случаях при построении модели исследуемых процессов полезно включать в нее и члены скользящего среднего, и авторегрессионные члены. Это приводит к смешанной модели АРСС (р, q): с (р + q + 2) неизвестными параметрами. Особый практический интерес представляет случай р = 1, q = 1.

Нестационарные модели Модель авторегрессии проинтегрированного скользящего среднего (АРПСС) предназначенная описывать нестационарные временные ряды, обладающие следующими свойствами: Анализируемый временной ряд включает в себя аддитивную составляющую , имеющую вид алгебраического полинома некоторой степени d-1 (d > 0); Ряд, получившийся из после применения к нему d-кратной процедуры последовательных разностей, может быть описан моделью АРСС(р, q)

Нестационарные модели Введем обобщенный авторегрессионный оператор Тогда модель можно записать таким образом: Модель является более общей и называется интегрированной моделью авторегрессии —скользящего среднего (АРПСС) порядка (р, d, q). Наиболее распространенные порядки модели: р = 0, d = 1, q = 1 р = 0 , d = 2, q = 2 р = 1, d = 1, q = 1 р = 1, d = 1, q = 0 р = 2 , d = 1, q = 0

Стационарность и обратимость процесса Процесс АР(р) является стационарным, если корни характеристического уравнения лежат вне единичного круга. На простом примере легко убедиться, что если корни лежат внутри единичного круга, то модель проявляет нестационарность. Особое внимание авторов модели привлек случай, когда корни лежат на единичной окружности. Так появилась не стационарная модель АРПСС. Условие обратимости для процесса СС(q) заключается в том, чтобы корни характеристического уравнения лежали вне единичного круга. Для процесса АРСС условия обратимости аналогичны

Автокорреляционная функция для АР Автокорреляционная функция в этом методе является основным инструментом при построении модели. Изучим ее свойства сначала для АР-процессов: Домножим выражение на и возьмем математическое ожидание. Тем самым получим разностное уравнение для автоковариаций: Отметим, что при k > 0. Разделим уравнение на : , при k > 0 (*) В общем случае автокорреляционная функция стационарного АР процесса будет состоять из смеси затухающих экспонент и затухающих синусоидальных волн.

Автокорреляционная функция для АР Имея коэффициенты автокорреляции, можно с их помощью оценить параметры АР процесса. Для этого подставим в (*) k = 1,2,..., р и получим систему линейных уравнений для : Это уравнения Юла-Уокера. Заменив теоретические автокорреляции на их оценки, можно получить оценки Юла-Уокера для параметров модели.

Автокорреляционная функция для CC Обратимся теперь к СС-процессам. Получим сначала автоковариационную функцию: Отсюда дисперсия процесса будет: и

Автокорреляционная функция для CC Следовательно, автокорреляционная функция будет: (**) Итак, для к > q автокорреляционная функция СС-процесса равна нулю. Другими словами, автокорреляционная функция процесса скользящей средней обрывается при лаге q. Это значит, что по автокорреляционной функции можно для процессов СС определить численное значение q. По оценкам , используя q уравнении (**), можно получить оценки . Однако в отличие от уравнений Юла-Уокера для AP-процессов, которые являются линейными, уравнения (**) являются нелинейными. Поэтому, за исключением простого случая, когда q - 1, эти уравнения должны решаться итеративно.

Частная автокорреляционная функция При построении модели вначале неизвестно, какого порядка авторегрессионный процесс надо ставить в соответствие фактическому ряду. Инструментом решения этого вопроса служит частная автокорреляционная функция. Здесь используется тот факт, что процесс АР (р), имеющий автокорреляционную функцию с бесконечным числом членов, по своей природе может быть описан с помощью р ненулевых функций от автокорреляций.

Частная автокорреляционная функция Для авторегрессионного процесса порядка р частная автокорреляционная функция будет отлична от нуля при k < р и равна нулю при k > р. Другими словами частная автокорреляционная функция АР (р)- процесса обрывается после лага р. Если значения параметров не слишком близки к границам нестационарности, то успешно могут быть использованы оценки Юла-Уокера; при невыполнении этого условия оценки оказываются грубыми.

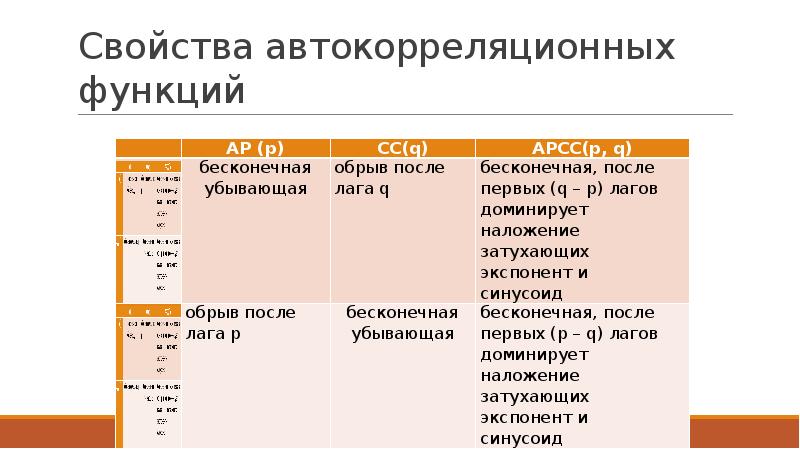
Свойства автокорреляционных функций