Осевая и центральная симметрии презентация

ОСЕВАЯ И ЦЕНТРАЛЬНАЯ Симметрии алгебра ΙΙ четверть

Содержание : Это интересно Высказывания о симметрии Простейшие виды симметрии Симметричность точек относительно прямой Симметричность двух точек относительно третьей Симметрия фигуры относительно точки Симметрия вокруг нас

Это интересно! Греческое слово симметрия буквально означает «соразмерность» Под симметрией в широком смысле понимают всякую правильность во внутреннем строении тела или фигуры Учение о различных видах симметрии представляет большую и важную ветвь в геометрии

Высказывания о симметрии «Симметрия — в широком или узком смысле в зависимости от того, как вы определите значение этого понятия,— является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство». Известный математик Генрих Вейль «Математик любит прежде всего симметрию» Максвелл Д. «Для человеческого разума симметрия обладает, по - видимому, совершенно особой притягательной силой» Фейнман Р.

Простейшие виды симметрии Зеркальная симметрия: две зеркально симметричные плоские фигуры всегда можно наложить друг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости Центральная симметрия: две центрально симметричные плоские фигуры всегда можно наложить друг на друга, не выводя их из общей плоскости. Для этого достаточно одну из них повернуть на угол 180 0 около центра симметрии Симметрия вращения: тело (или фигура) обладает симметрией вращения, если при повороте на некоторый угол около некоторой прямой АВ (ось симметрии) оно полностью совмещается со своим исходным положением

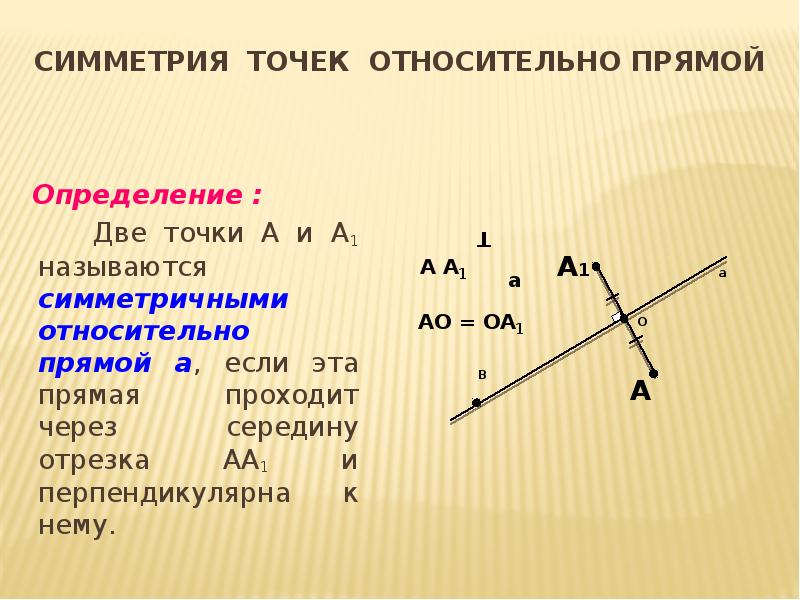
Симметрия точек относительно прямой Определение : Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.

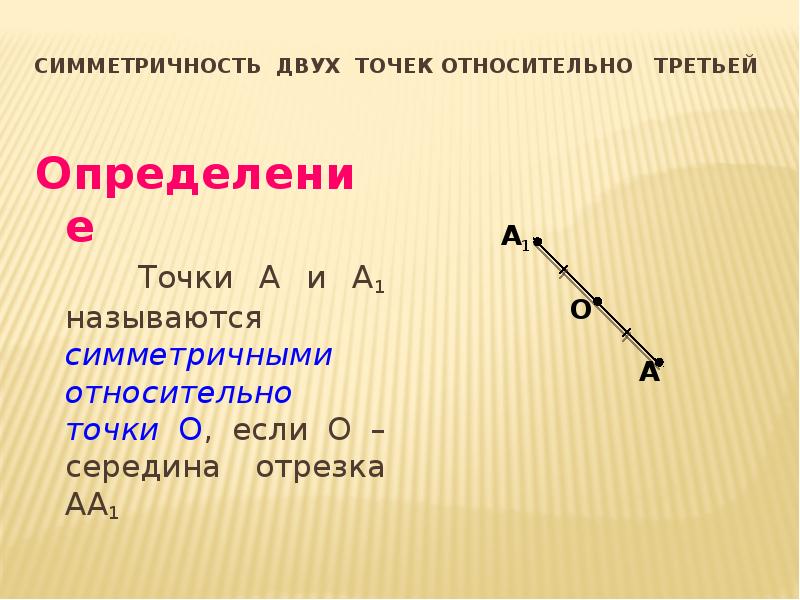
Симметричность двух точек относительно третьей Определение Точки A и A1 называются симметричными относительно точки О, если О – середина отрезка AA1

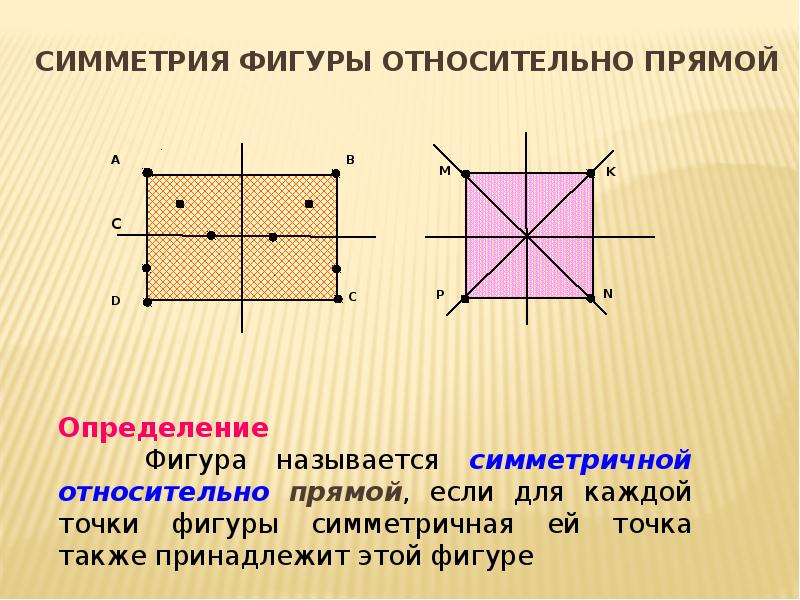
Симметрия фигуры относительно Прямой

Симметрия в искусстве

Симметрия в технике

Симметрия в архитектуре

Симметрия в природе

Симметрия в литературе Палиндром - это абсолютное проявление симметрии в литературе Например: «А луна канула» «А роза упала на лапу Азора»

Конец сделано ученицей 8 Б класса Казаковой Ольгой