Основные понятия математической статистики презентация

Основные понятия математической статистики Тишков Артем Валерьевич, к.ф.-м.н., доцент Микрюкова Надежда Николаевна

Основные понятия математической статистики. Математическая статистика – это раздел математики о методах регистрации, систематизации и анализа статистических экспериментальных данных, полученных в результате наблюдения массовых случайных явлений. Статистическая совокупность – это множество объектов, обладающих общими признаками, которые являются наиболее важными (типичными) для характеристики этих объектов. Серия измерений какого либо признака совокупности – это совокупность значений случайной величины. Объём совокупности N –это число членов совокупности.

Генеральная совокупность – это совокупность всех объектов, которые имеют типичную характеристику или признак. Это все возможные значения случайной величины. Генеральная совокупность – это совокупность всех объектов, которые имеют типичную характеристику или признак. Это все возможные значения случайной величины. Выборочная совокупность (выборка) – это отобранная тем или иным способом часть генеральной совокупности. Из одной генеральной совокупности можно отбирать сколь угодно много выборок, главное, чтобы выборка была репрезентативной (представительной), а для этого элементы выборки должны отбираться случайным образом. Варианта – это числовое значение изучаемого признака( отдельные значения случайной величины).

Основные задачи, которые стоят перед математической статистикой: 1. Определение закона распределения случайной величины по имеющимся статистическим данным ( по выборке – закон распределения для всей генеральной совокупности). 2. Определение неизвестных параметров распределения ( по выборке оценить параметры генеральной совокупности). 3. Задача проверки правдоподобия выдвигаемых статистических гипотез.

Схема предварительной обработки экспериментальных данных. 1) Сбор экспериментальных данных. Чтобы определить закон распределения случайной величины, нужно провести серию измерений или подсчётов для интересующей нас случайной величины (признака). В результате получаем статистический ряд – это совокупность числовых данных или выборка объёмом n: Затем производят упорядочивание членов выборки – эта операция называется ранжирование. Ранжирование -- это расположение всех имеющихся вариант по возрастанию. Получаем ранжированный статистический ряд.

Пример: При измерении частоты пульса у 10 пациентов получены следующие результаты: 90, 110, 65, 80, 90, 60, 70, 80, 70, 80 Ранжированный ряд имеет вид: 60, 65, 70, 70, 80, 80, 80, 90, 90, 110. Колебания изучаемого признака называются варьирование. В нашем примере варьирование - это изменение частоты пульса.

Схема предварительной обработки экспериментальных данных. 2) Составление вариационного ряда. вариационный ряд (статистическое распределение) -- набор пар значение – частота, с которой это значение встретилось в выборке. Если случайная величина изменяется дискретно, то составляем дискретный вариационный ряд.

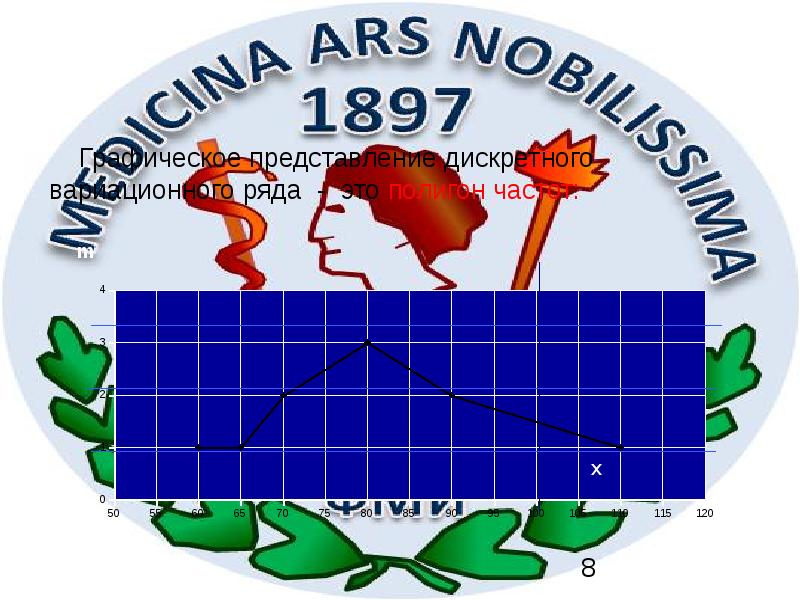
Графическое представление дискретного вариационного ряда - это полигон частот: Графическое представление дискретного вариационного ряда - это полигон частот:

Если признак изменяется непрерывно, то составляется интервальный вариационный ряд: набор пар вид интервал – частота. Если признак изменяется непрерывно, то составляется интервальный вариационный ряд: набор пар вид интервал – частота. Для построения интервального вариационного ряда выборку разбивают на интервалы. Есть несколько рекомендаций по вычислению числа интервалов: k=log2n+1 (формула Стерджесса), k=√n и др , подробнее см. http://ami.nstu.ru/~headrd/seminar/publik_html/Z_lab_8.htm Длина интервала ΔX рассчитывается по формуле:

Контрольные вопросы. 1.Равномерный закон распределения непрерывной случайной величины. 2.Нормальный закон распределения непрерывной случайной величины. 3.Основные понятия математической статистики. 4.Схема предварительной обработки экспериментальных данных. 5.Статистические характеристики совокупности. 6.Ошибка среднего арифметического. 7.Доверительный интервал и доверительная вероятность. 8.Распределение Стьюдента.