Основы логики. Таблица истинности. Равносильные логические выражения презентация
Содержание
- 2. Логика – это наука о формах и способах мышления
- 3. Содержание Формы мышления Алгебра высказываний Логические выражения, операции и таблицы
- 4. 1. Формы мышления
- 5. 1.1. Понятие Понятие – это форма мышления, отражающая основные, наиболее существенные
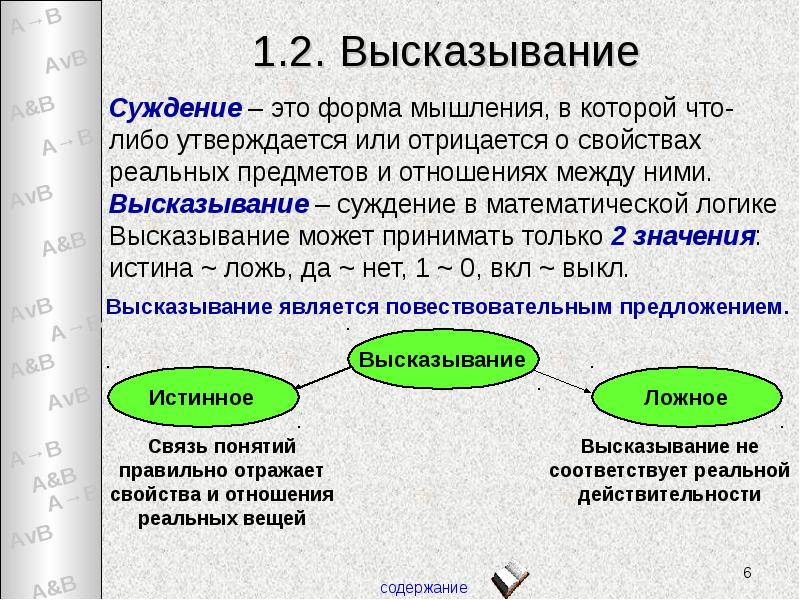
- 6. 1.2. Высказывание
- 7. Какие из предложений являются высказыванием?
- 8. Определи истинность высказываний
- 9. Простые и сложные высказывания
- 10. 1.3. Утверждение
- 11. 1.4. Умозаключение
- 12. 1.5. Логическое выражение
- 13. 2. Алгебра высказываний Алгебра высказываний служит для определения истинности или ложности
- 14. Высказывания могут быть простыми и сложными. Высказывания могут быть простыми и
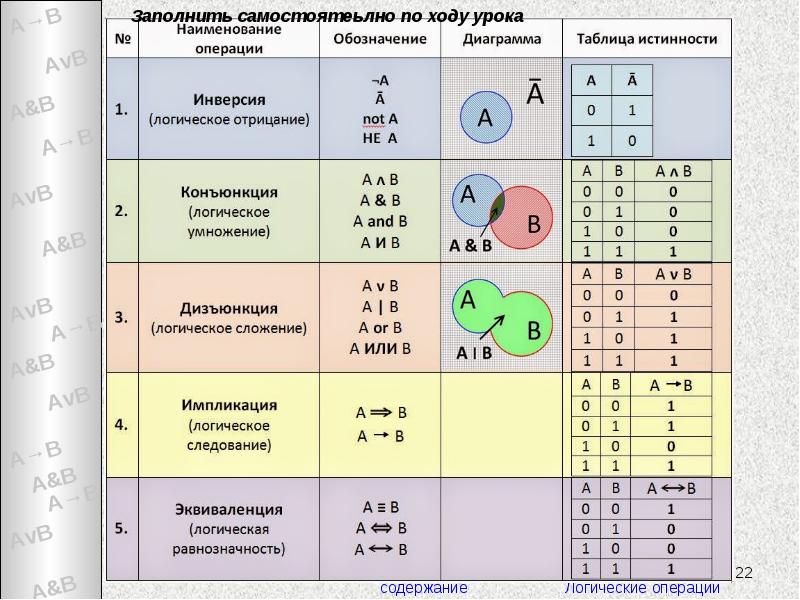
- 15. Логические операции
- 16. 2.1. Логическое умножение (конъюнкция)
- 17. 2.2. Логическое сложение (дизъюнкция)
- 18. 2.3. Логическое отрицание (инверсия)
- 19. 2.4. Логическое следование (импликация) Соответствует обороту Если…, то… (из А следует
- 20. 2.5. Логическое равенство (эквивалентность)
- 21. 2.5. Логическое сложение по модулю 2 (исключающее ИЛИ)
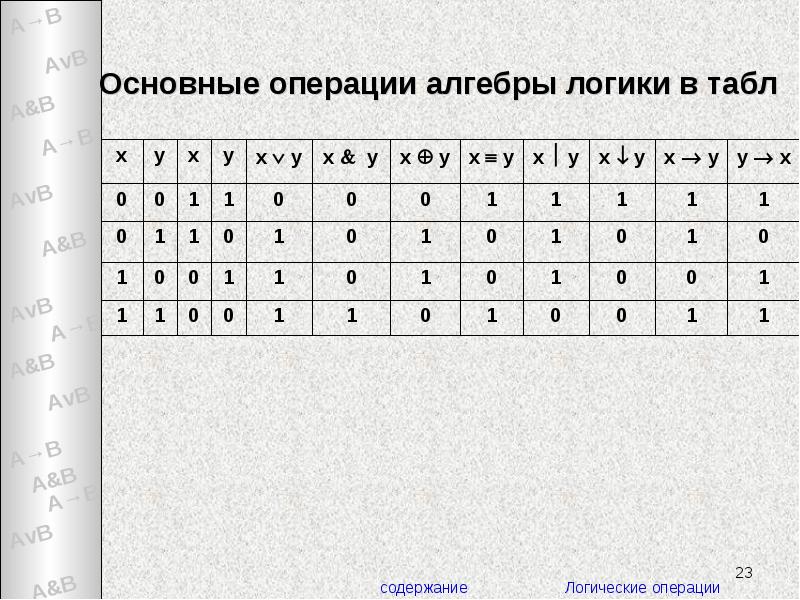
- 23. Основные операции алгебры логики в табл
- 24. 3. Логические выражения
- 25. Найдите значения логических выражений
- 27. Построение таблицы истинности
- 28. Построение таблицы истинности
- 29. ПРИМЕР: составить таблицу истинности для сложного логического выражения
- 30. ПРИМЕР: составить таблицу истинности для сложного логического выражения D = неA
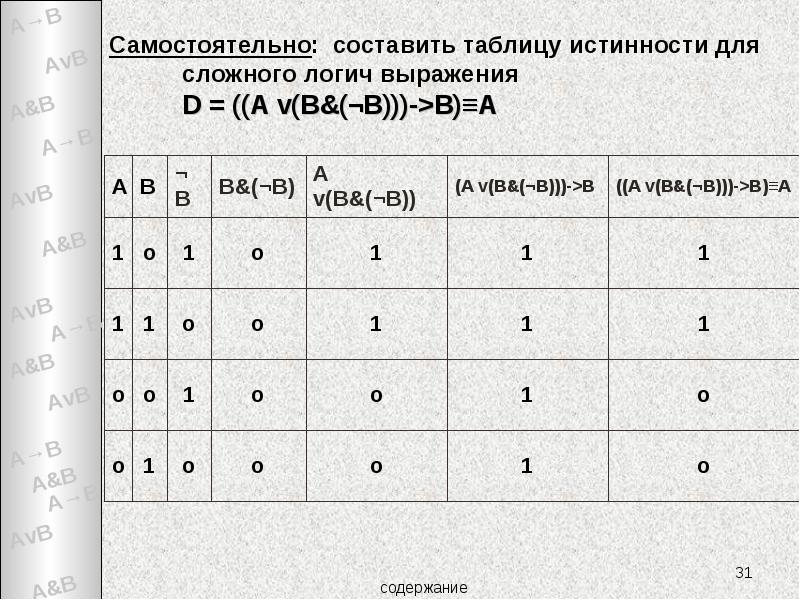
- 31. Самостоятельно: составить таблицу истинности для сложного логич выражения D = ((А
- 32. Задание. Составить таблицы истинности для сложных логич выражений А(¬¬С) а+(в+¬в¬с)
- 33. Задание: Дан фрагмент таблицы истинности логического выражения F от трех аргументов:
- 34. Равносильные логические выражения
- 35. Докажи равносильность выражений: Докажи равносильность выражений: А+В+С=В+С+А АВС=ВСА
- 36. Выражение называется тождественно ложным (истинным), если оно принимает значение 0 (1)
- 37. 5. Домашнее задание Даны высказывания: A = «р делится на 5»
- 38. 2. Составьте и запишите истинные сложные высказывания из простых с использованием
- 39. Доп дом задание ●какое тождество записано неверно х+¬х=1, х+х+х+х+х+х+х=1, ххххххх=1 ●дай
- 40. Проверь себя Задание 1 Задание 2 Задание 3 Задание 4 Задание
- 41. Задание 1 Расставь соответствующие номера Логика Высказывание Алгебра логики Логическая константа
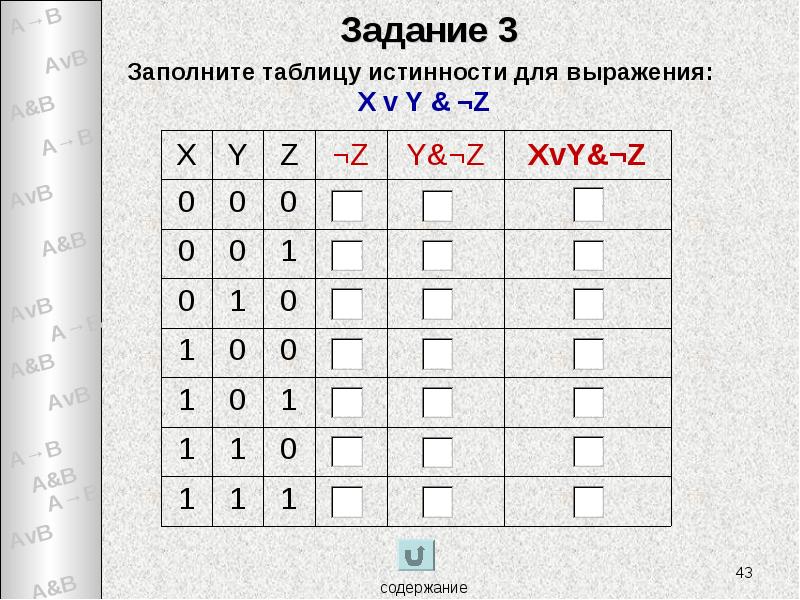
- 43. Задание 3
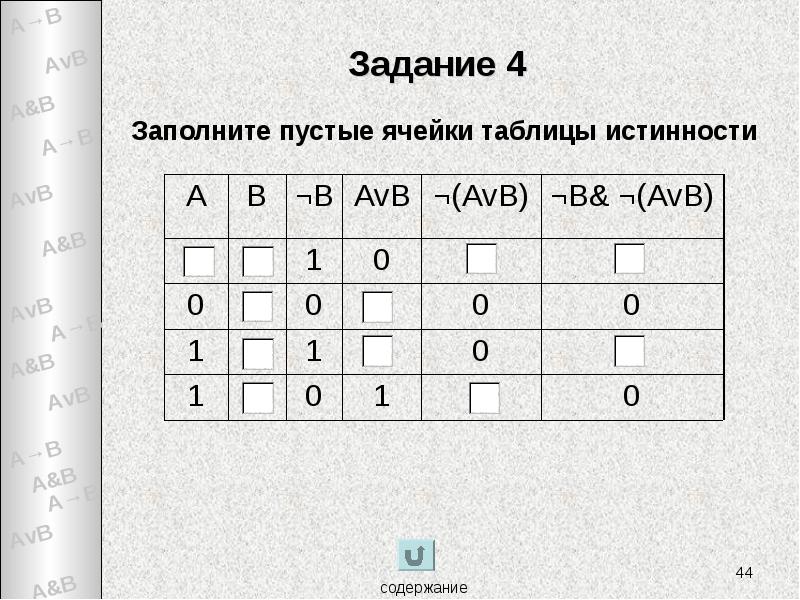
- 44. Задание 4
- 49. Скачать презентацию










































Слайды и текст этой презентации
Скачать презентацию на тему Основы логики. Таблица истинности. Равносильные логические выражения можно ниже:
Похожие презентации





























