Основы векторной алгебры. Векторы на плоскости и в пространстве презентация
Содержание
- 2. 1. ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
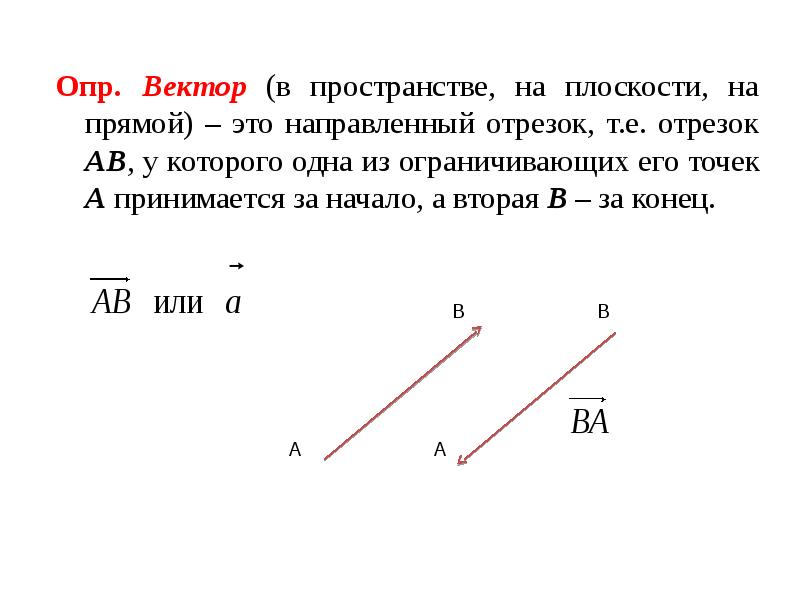
- 3. Опр. Вектор (в пространстве, на плоскости, на прямой) – это направленный
- 4. Опр. Ненулевые векторы называются равными:
- 5. Сложение векторов Пусть - два произвольных вектора. Возьмем произвольную
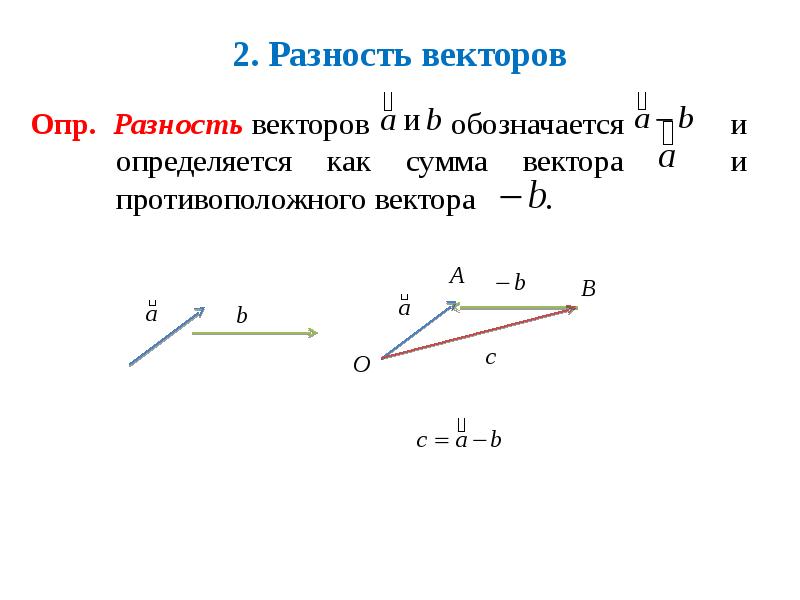
- 6. 2. Разность векторов Опр. Разность векторов обозначается
- 7. 3. Умножение вектора на число Опр. Произведение вектора на число
- 8. Опр. Два вектора называются коллинеарными, если они лежат на
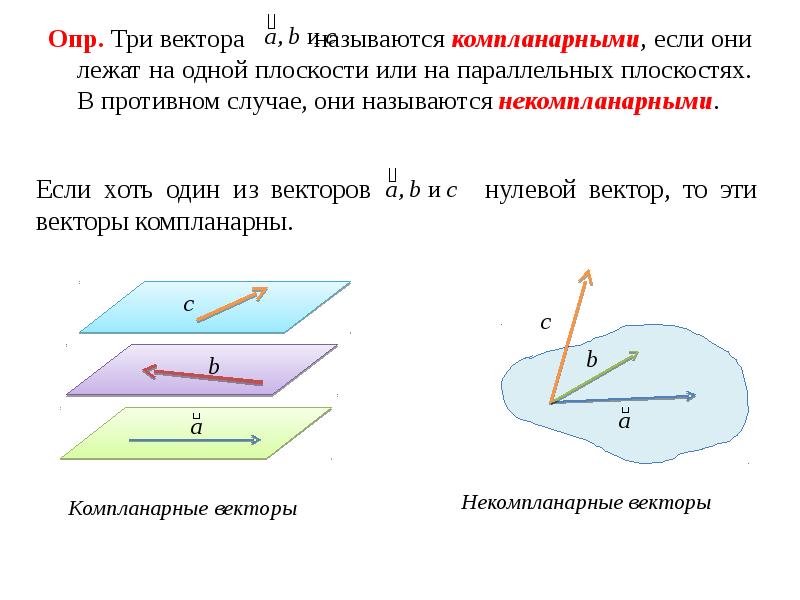
- 10. Опр. Три вектора называются компланарными, если они лежат на
- 11. Множество всех свободных векторов на прямой будем обозначать R1, на плоскости
- 12. Опр. Опр. 1) Базисом в пространстве называются любые 3 некомпланарных вектора,
- 13. Опр. Если - базис в пространстве и
- 14. Опр. Если - некоторая система векторов пространства R
- 15. Опр. Векторы называются линейно зависимыми, если существует такая линейная комбинация
- 16. Свойства Если среди векторов есть нулевой вектор, то эти векторы линейно
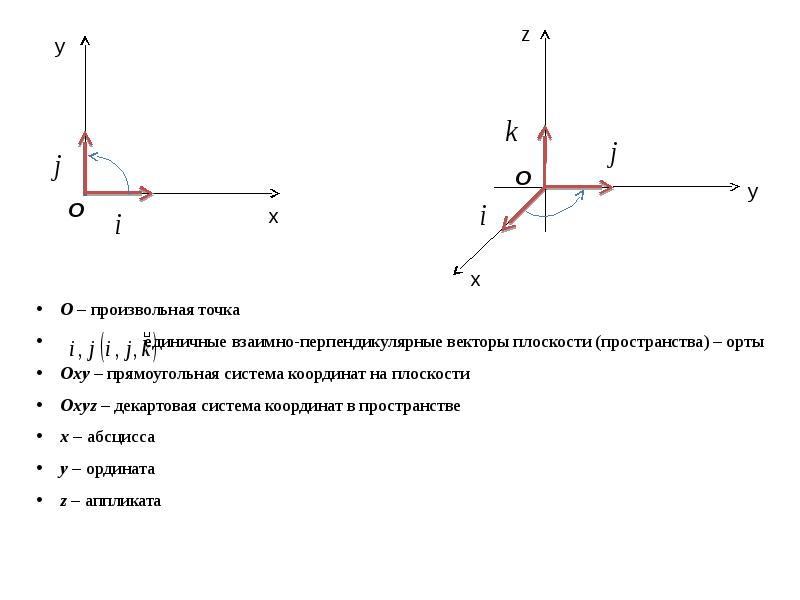
- 17. 2. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
- 18. О – произвольная точка О – произвольная точка
- 20. Задача 1. Найти координаты вектора, если даны координаты его начальной и
- 21. Условие коллинеарности двух векторов Векторы
- 23. Линейные операции над векторами в координатной форме
- 24. Направление вектора определяется углами α, β, γ, образованными с осями координат
- 25. 3. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 26. Опр. Скалярным произведением двух векторов называется число, обозначаемое
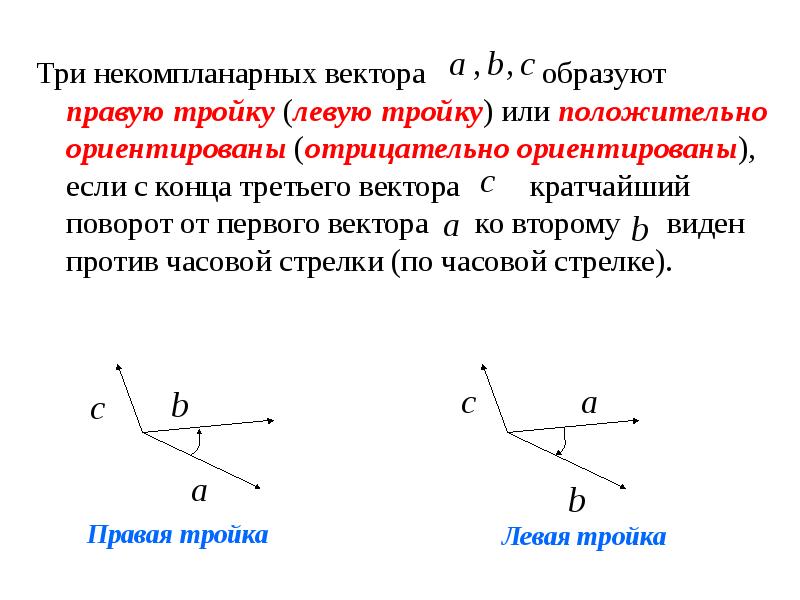
- 31. Три некомпланарных вектора образуют правую тройку (левую тройку)
- 32. Векторное произведение векторов Опр. Векторным произведением двух векторов
- 33. Обозначения:
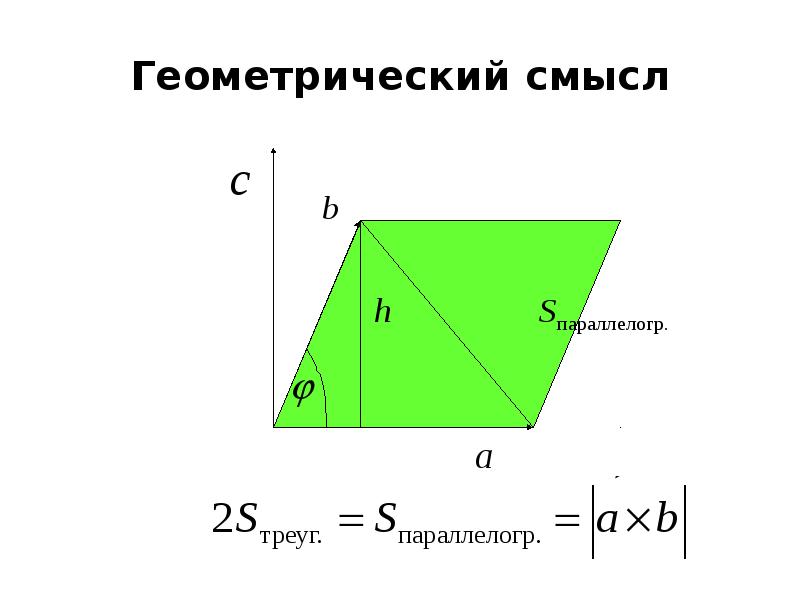
- 34. Геометрический смысл
- 35. Свойства
- 36. 6. Теорема (запись векторного произведения в координатах) Если
- 37. Смешанное произведение векторов Опр. Смешанным произведением трех векторов
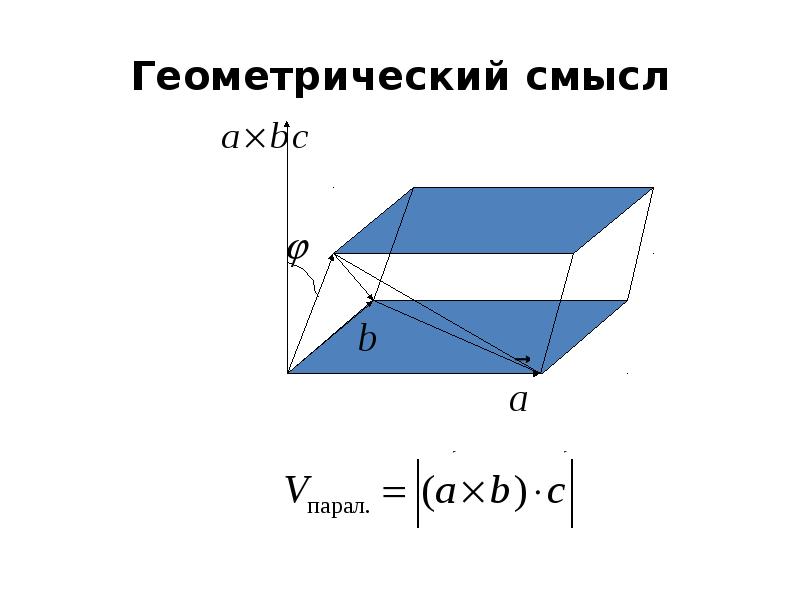
- 38. Геометрический смысл
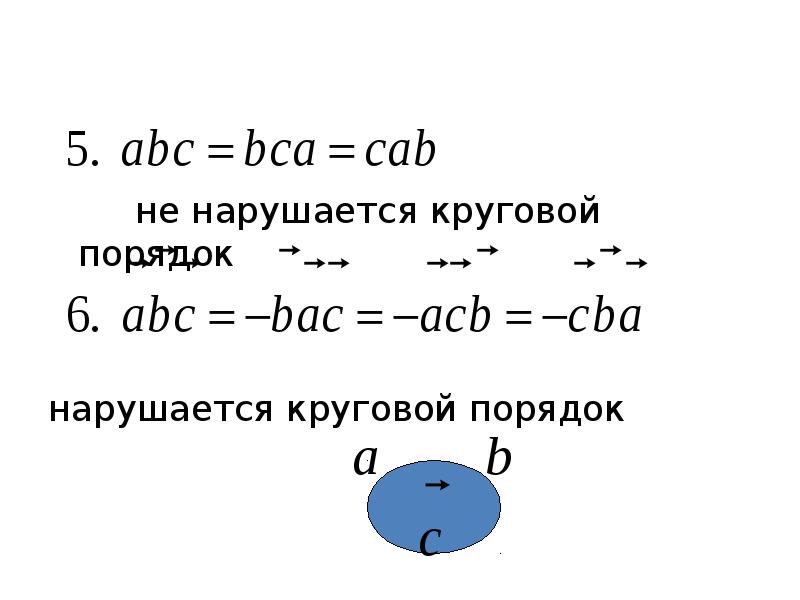
- 39. Свойства
- 40. не нарушается круговой порядок нарушается круговой порядок
- 41. 7. Теорема (запись смешанного произведения в координатах) Если
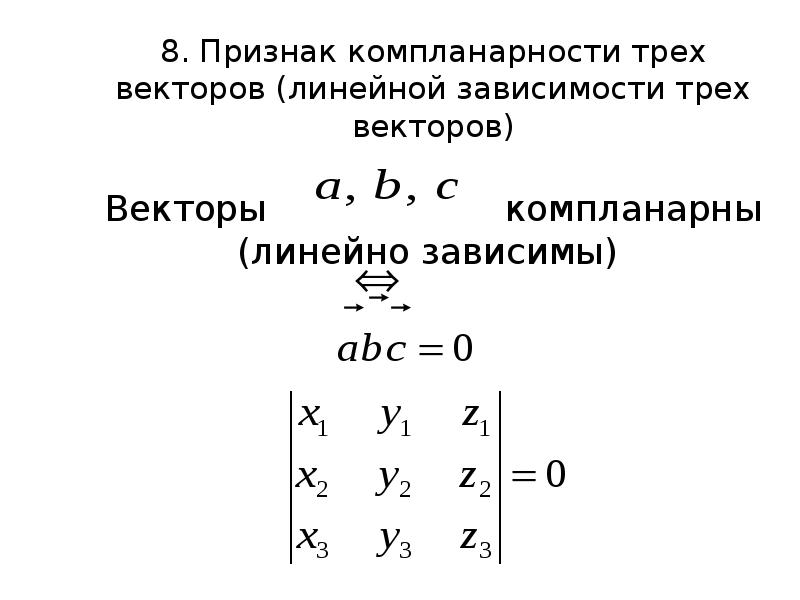
- 42. 8. Признак компланарности трех векторов (линейной зависимости трех векторов) Векторы
- 43. Скачать презентацию































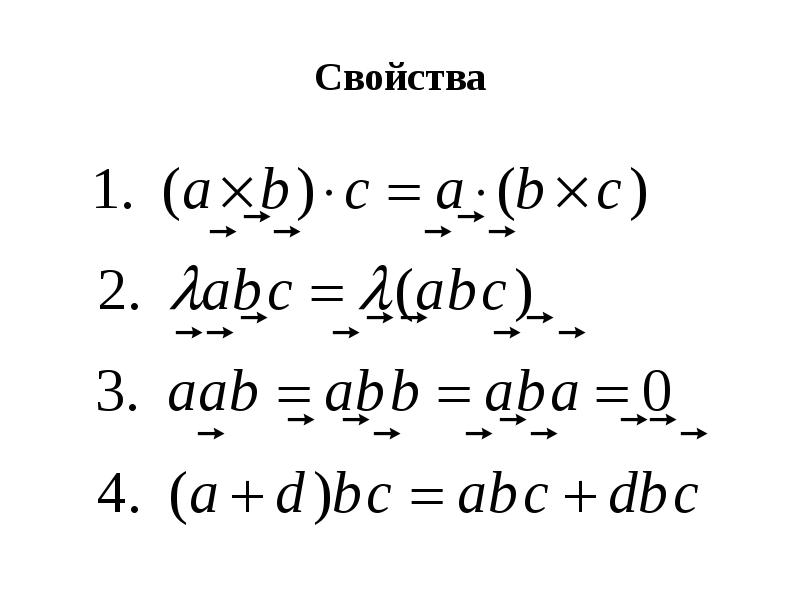

Слайды и текст этой презентации
Скачать презентацию на тему Основы векторной алгебры. Векторы на плоскости и в пространстве можно ниже:
Похожие презентации





























