Перестановки. Построение перестановки по таблице инверсий. (Лекция 6) презентация

Лекция 6 Перестановки

Перестановки Перестановкой порядка N называется расположение N различных объектов в ряд в некотором порядке. Например, для трех объектов — а, b и с — существует шесть перестановок: аbс, acb, bac, bса. cab, cba. Для множества из N элементов можно построить N! различных перестановок: первую позицию можно занять N способами, вторую — (N – 1) способом, так как один элемент уже занят, и т. д. На последнее место можно поставить только один оставшийся элемент. Следовательно, общее количество вариантов расстановки равно N  (N −1)  (N − 2)  ...  1 = N! Далее будем рассматривать перестановки элементов множества {1, 2, 3, … , N}

Инверсии Пусть даны базовое множество из N элементов 1,2, 3,..., N и его перестановка Пара называется инверсией (инверсионной парой) перестановки , если при i < j. Например, перестановка 4, 1, 3, 2 имеет четыре инверсии: (4,1), (3,2), (4,3) и (4,2). Единственной перестановкой, не содержащей инверсий, является упорядоченная перестановка 1, 2, 3, ... , N. Таким образом, каждая инверсия — это пара элементов перестановки, нарушающих ее упорядоченность.

Таблицей инверсий перестановки a1,a2, ...,aN называется последовательность чисел b1, b2 …, bN , где bj есть число элементов перестановки, больших j и расположенных левее j Таблицей инверсий перестановки a1,a2, ...,aN называется последовательность чисел b1, b2 …, bN , где bj есть число элементов перестановки, больших j и расположенных левее j (т. е. количество инверсий вида (x, j), при x > j). Например, для перестановки 5 9 1 8 2 6 4 7 3 таблица инверсий: 2 3 6 4 0 2 2 1 0. Свойство элементов таблицы инверсий: bN = 0, … 0 ≤ bi ≤ N – i , … 0 ≤ b1 ≤ N – 1. Утверждение Таблица инверсий единственным образом определяет соответствующую ей перестановку.

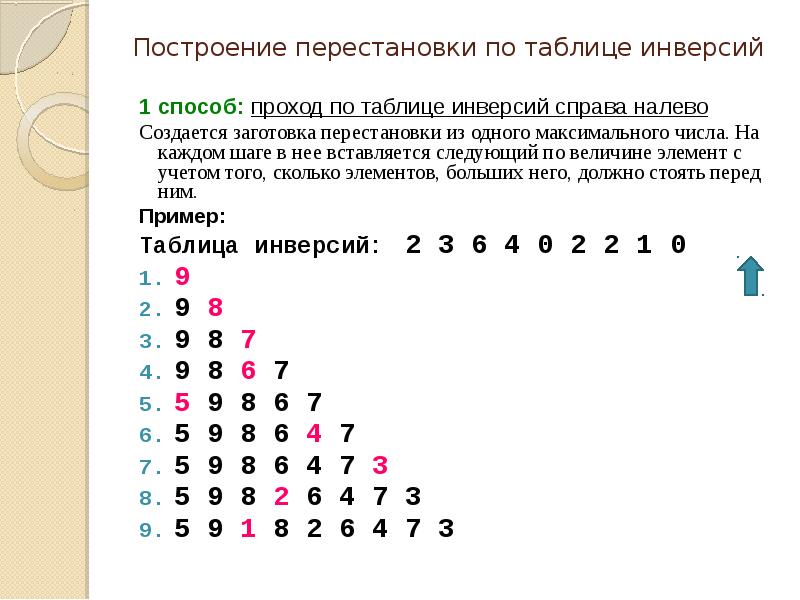
Построение перестановки по таблице инверсий 1 способ: проход по таблице инверсий справа налево Создается заготовка перестановки из одного максимального числа. На каждом шаге в нее вставляется следующий по величине элемент с учетом того, сколько элементов, больших него, должно стоять перед ним. Пример: Таблица инверсий: 2 3 6 4 0 2 2 1 0 9 9 8 9 8 7 9 8 6 7 5 9 8 6 7 5 9 8 6 4 7 5 9 8 6 4 7 3 5 9 8 2 6 4 7 3 5 9 1 8 2 6 4 7 3

Алгоритм П1: построение перестановки по таблице инверсий справа налево Вход: N > 0 - количество элементов перестановки, b1, b2 …, bN – таблица инверсий, 0 ≤ bj ≤ N − j. Р := пустая последовательность; цикл по j от N вниз до 1 вставить число j в Р после bj элементов; конец цикла; Выход: Р − перестановка, соответствующая данной таблице инверсий

Построение перестановки по таблице инверсий 2 способ: проход по таблице инверсий слева направо Создается заготовка пустой перестановки длины N. На каждом шаге для каждого элемента перестановки, начиная с 1, отсчитывается в ней столько пустых ячеек, какое число записано в соответствующей позиции в таблице инверсий. В следующее за ними пустое место вставляется этот элемент. Пример: Таблица инверсий: 2 3 6 4 0 2 2 1 0 Перестановка:

Алгоритм П2: построение перестановки по таблице инверсий слева направо Вход: N > 0 - количество элементов перестановки, b1, b2 …, bN – таблица инверсий, 0 ≤ bj ≤ N − j. Р := последовательность из N пустых элементов; цикл по i от 1 до N с шагом 1 выполнять пропустить bi пустых мест в P; поместить i на следующее пустое место; конец цикла Выход: Р − перестановка, соответствующая данной таблице инверсий

Инверсионный метод поиска всех перестановок Таблица инверсий однозначно определяет перестановку и каждая перестановка имеет только одну таблицу инверсий. Следовательно, если мы сумеем перебрать все таблицы инверсий, то с помощью алгоритмов П1 или П2 сможем по ним восстановить все перестановки. Рассмотрим таблицу инверсий как N-значное число в такой необычной «системе счисления»: количество цифр, которое можно использовать в i-м разряде (с конца, начиная с 0) равно i. Возьмем «минимальную» таблицу и будем последовательно прибавлять к ней, как к числу, единицу, пользуясь, например, алгоритмом сложения с переносом для многоразрядных чисел, модифицированным для нашей «системы счисления».

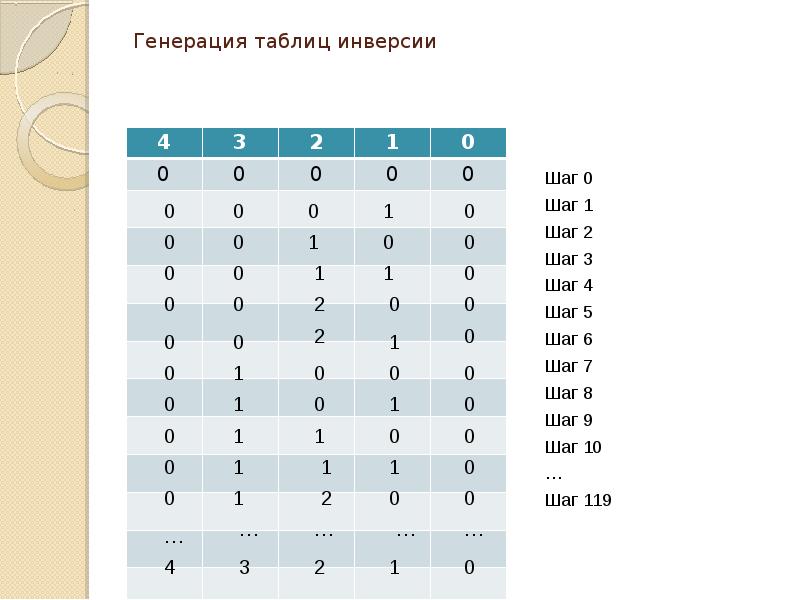
Генерация таблиц инверсии

Алгоритм И1: нахождение следующей таблицы инверсий Пусть B = b1, b2, ..., bN – таблица инверсий, построенная на предыдущем шаге. Тогда следующая таблица инверсий получается из нее прибавлением к ней единицы: i := N; flag := истина; пока flag выполнять x := bi + 1; если x > N – i то начало bi := 0; i := i –1; конец иначе начало bi := x; flag := ложь; конец конец пока

Алгоритм Дейкстры: поиск следующей по алфавиту перестановки Пусть даны две перестановки b = b1, b2 …, bN и c = c1, c2 …, cN набора 1, 2, ..., N. Говорят, что перестановка b предшествует перестановке с в алфавитном (лексико­графическом) порядке, если для минимального значения k, такого что bk ≠ ck, справедливо bk < сk. Например, перестановка 1 2 3 4 5 предшествует перестановке 1 2 4 5 3 (здесь k = 3). Первой перестановкой в алфавитном порядке является перестановка 1,2,3, ..., N, а последней — N,N-1,N-2,...,1

Идея алгоритма Дейкстры: определить каким-либо образом функцию, которая по заданной перестановке выдает непосредственно следующую за ней в алфавитном порядке, и применять ее последовательно к собственным результатам начиная с самой первой перестановки, пока не будет получена последняя. Например, для перестановки 1 4 6 2 9 5 8 7 3 следующей по алфавиту является перестановка 1 4 6 2 9 7 3 5 8.

Алгоритм Дейкстры: генерация следующей по алфавиту перестановки Вход: N > 0 — количество элементов; a1, a2, …, aN-1, aN – предыдущая перестановка. Шаг 1. Просматривая перестановку, начиная с последнего элемента, найдем такой номер i, что ai+1 > ... > aN и ai < ai+1. Если такого i нет, то последовательность упорядочена по убыванию и следующей перестановки нет: конец алгоритма. Шаг 2. Найти в «хвосте» ai+1, …, aN элемент aj,, такой что i+1  j  N, aj есть наименьшее значение, удовлетворяющее условию aj > ai. После этого поменять местами ai и aj . Шаг 3. Упорядочить «хвост» ai+1, …, aN по возрастанию. Для этого достаточно его инвертировать (обернуть в обратном порядке). Выход: следующая по алфавиту перестановка за данной.

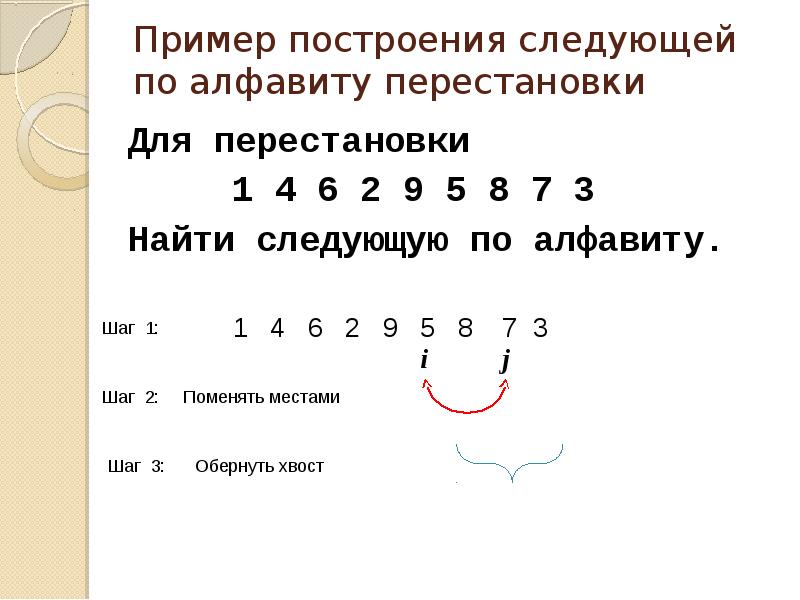
Пример построения следующей по алфавиту перестановки Для перестановки 1 4 6 2 9 5 8 7 3 Найти следующую по алфавиту.

Рекурсивный метод поиска всех перестановок Метод рекурсивного перебора перестановок основан на идее сведения исходной задачи к аналогичной задаче на меньшем наборе входных данных. Система рекуррентных соотношений, определяющих множество Реr(М) всех перестановок базового множества М произвольной природы: Реr(0) = {""}, Реr(М) = Permut(i, M\{i}), Permut(i, S) = {"i" + s  s  Per(S) }. Первое равенство задает условие обрыва рекурсивного спуска: пустое множество элементов порождает пустую перестановку. Два последних равенства определяют правила рекурсивного перехода.

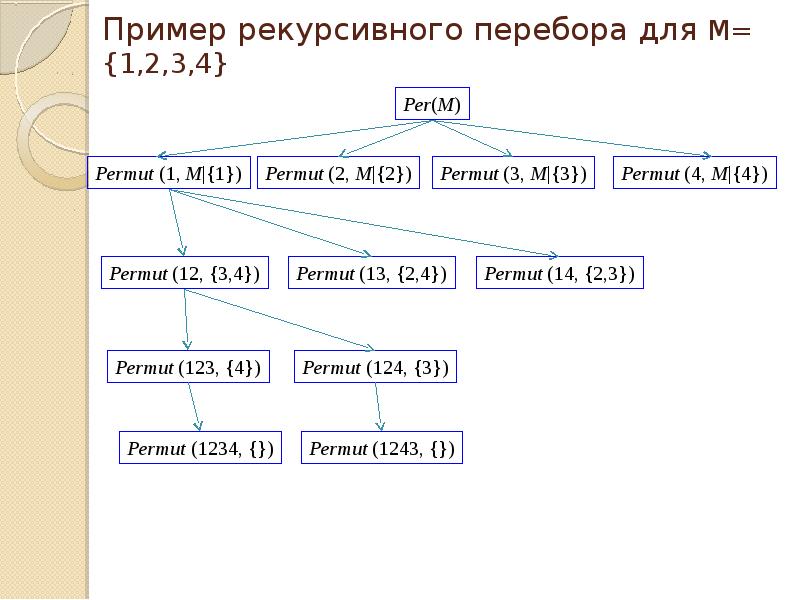
Пример рекурсивного перебора для M= {1,2,3,4}

На языке Си этот процесс можно описать следующим образом: typedef char string[256]; void permut(string start, string rest) { int lenr = strlen(rest); int lens = strlen(start); int i=0; string sl=“"; string s2=“"; if (lenr == 0) Printf(“%s\n”, start); else { for (i = 0; i < lenr; i++) { /* Добавляем i-ый символ к строке start */ strcpy(sl,start); strncpy(sl+lens,rest+i,1); strncpy(sl+lens+1,"\0",1); /* Удаляем i-ый символ из строки rest */ strncpy(s2,rest,i); strncpy(s2+i,rest+i+l,lenr-i-1); strncpy(s2+lenr-l,"\0", 1); /* Рекурсивный переход */ permut( s1, s2 ); } } }

Генерация всех перестановок методом Кнута Идея: если построены все перестановки длины N, то для каждой такой перестановки можно построить N+1 перестановку длины N+1. Пример: Для перестановки 3241 можно построить 5 различных перестановок длины 5: 53241 35241 32541 32451 32415

Генерация перестановок методом Кнута – 1 способ Пусть дана перестановка длины N. Дописать в конец перестановки числа (2i+1)/2 (0  i  N). Перенумеровать элементы полученных перестановок в порядке их возрастания. Пример: дана перестановка 3241. 3 2 4 1 0.5  4 3 5 2 1 3 2 4 1 1.5  4 3 5 1 2 3 2 4 1 2.5  4 2 5 1 3 3 2 4 1 3.5  3 2 5 1 4 3 2 4 1 4.5  3 2 4 1 5

Генерация перестановок методом Кнута – 2 способ Пусть дана перестановка длины N: a1 a2 … aN . Дописать в конец перестановки числа k (1  k  N +1). Для всех ai  k заменить их на ai + 1. Пример: дана перестановка 3241. 3 2 4 1 1  4 3 5 2 1 3 2 4 1 2  4 3 5 1 2 3 2 4 1 3  4 2 5 1 3 3 2 4 1 4  3 2 5 1 4 3 2 4 1 5  3 2 4 1 5

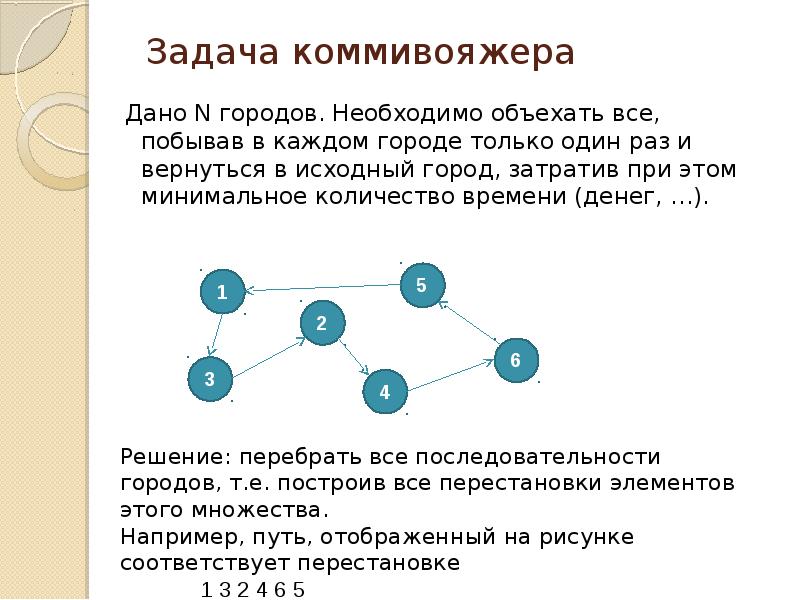
Задача коммивояжера Дано N городов. Необходимо объехать все, побывав в каждом городе только один раз и вернуться в исходный город, затратив при этом минимальное количество времени (денег, …).