Применение производной к исследованию функций презентация
Содержание
- 2. Как родилась производная Великий французский математик Пьер Ферма в 1629 году
- 3. Как родилась производная
- 4. Как родилась производная
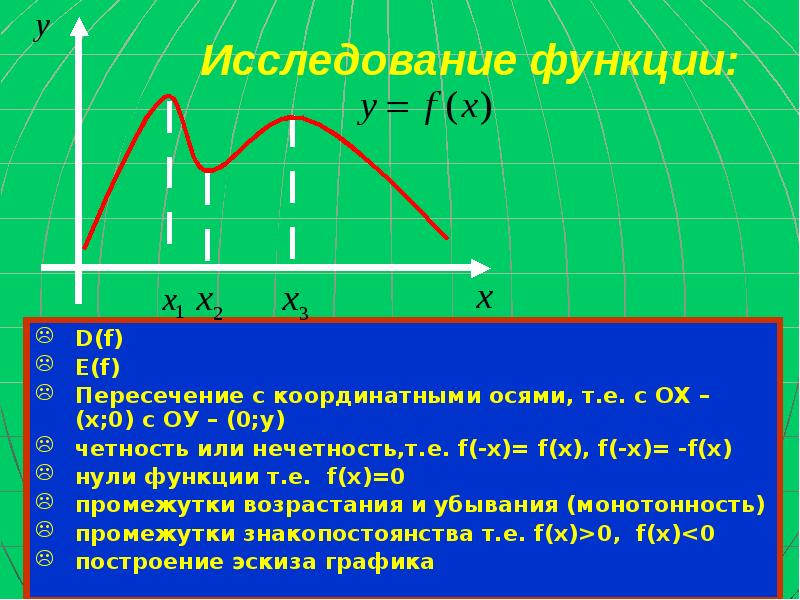
- 5. Исследование функции: D(f) E(f) Пересечение с координатными осями, т.е. с ОХ
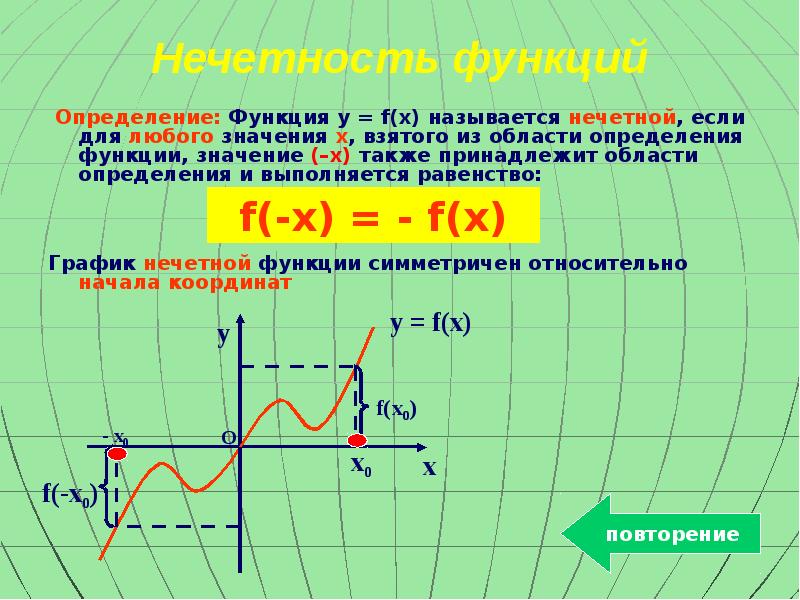
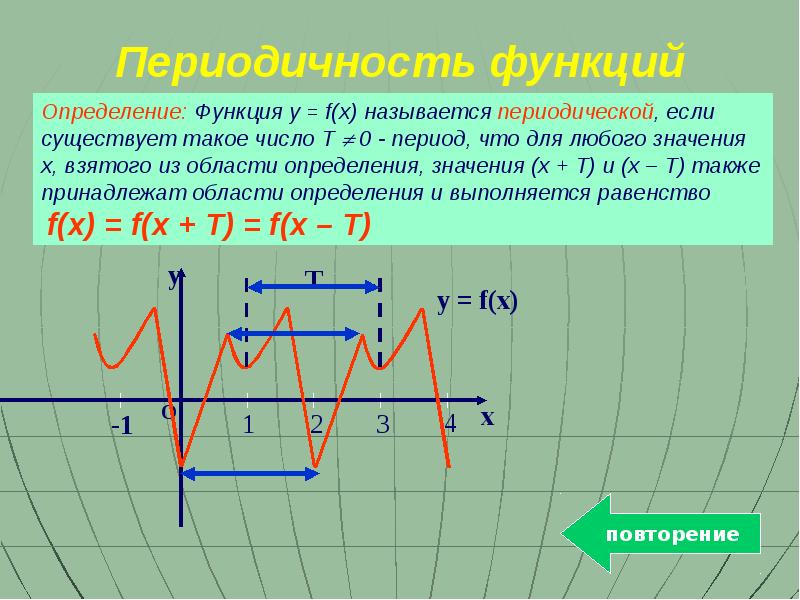
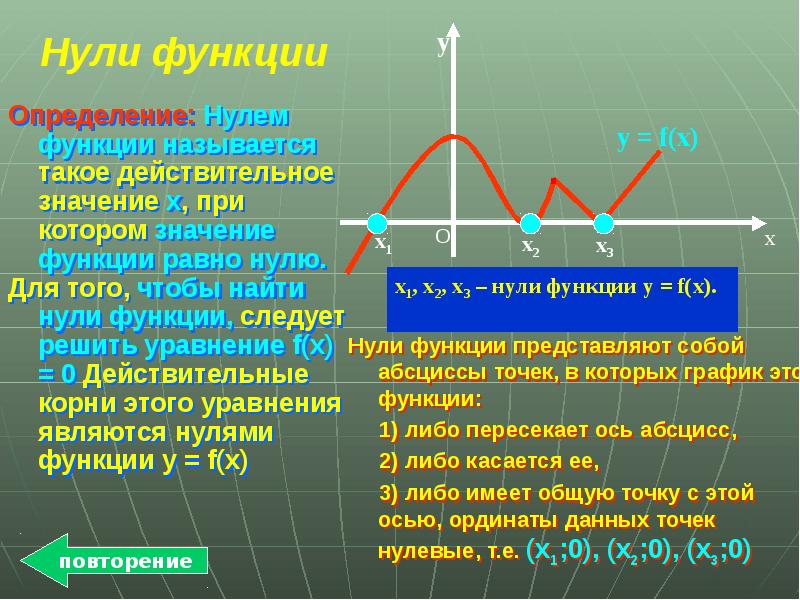
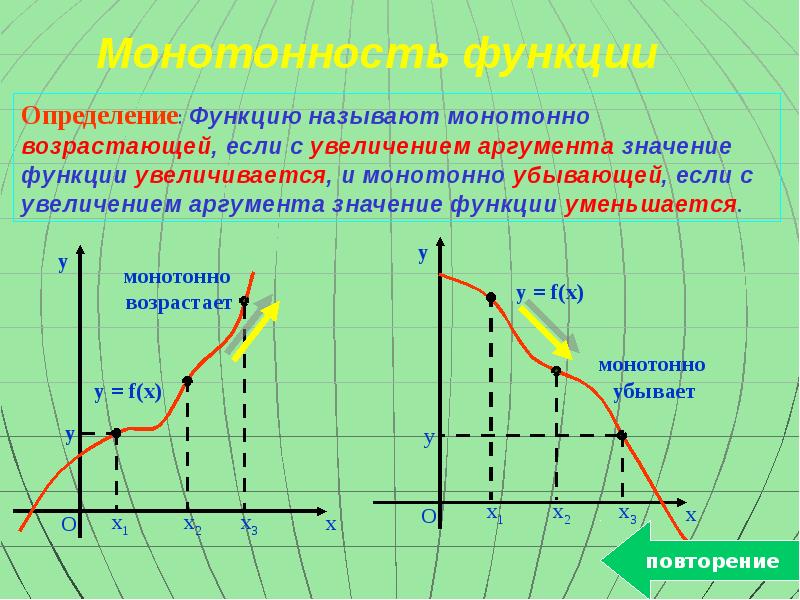
- 6. Повторение Четность, нечетность функций Периодичность Нули функции Промежутки знакопостоянства Монотонность функции
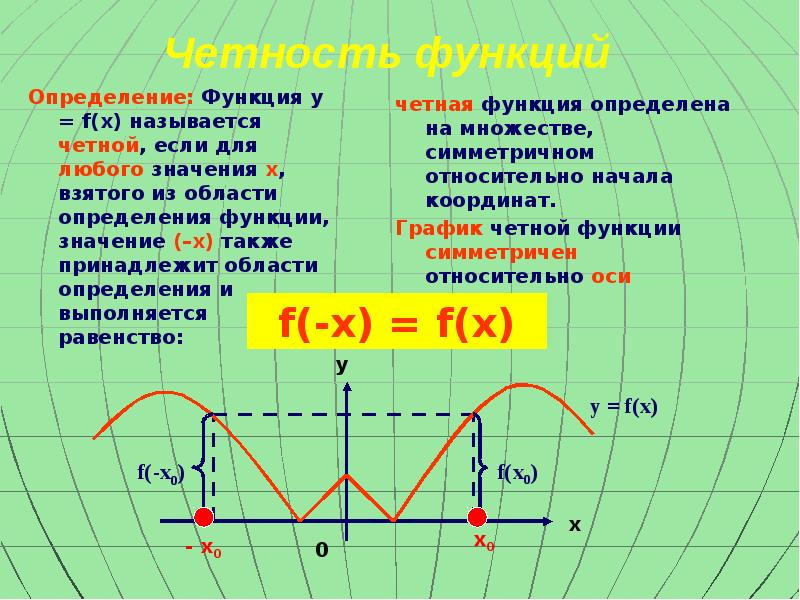
- 7. Четность функций Определение: Функция y = f(x) называется четной, если для
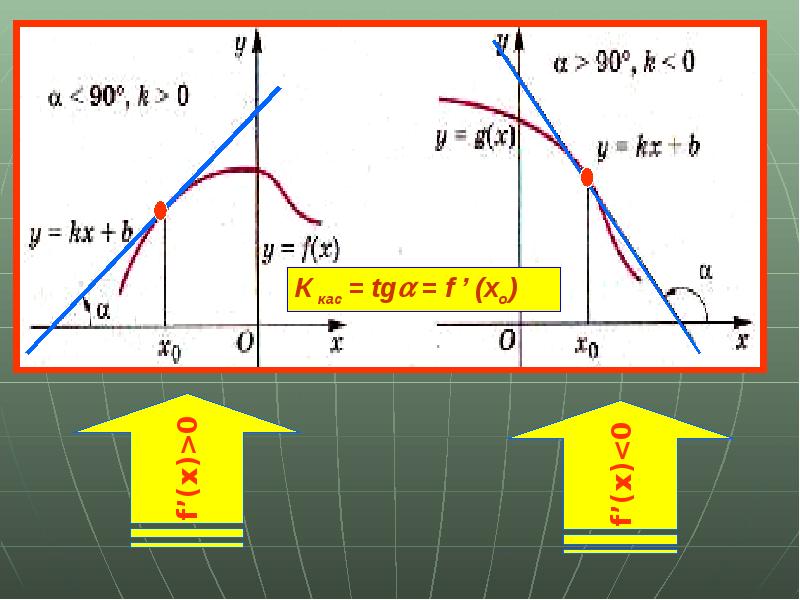
- 13. Если производная функции в каждой точке некоторого промежутка положительна, то функция
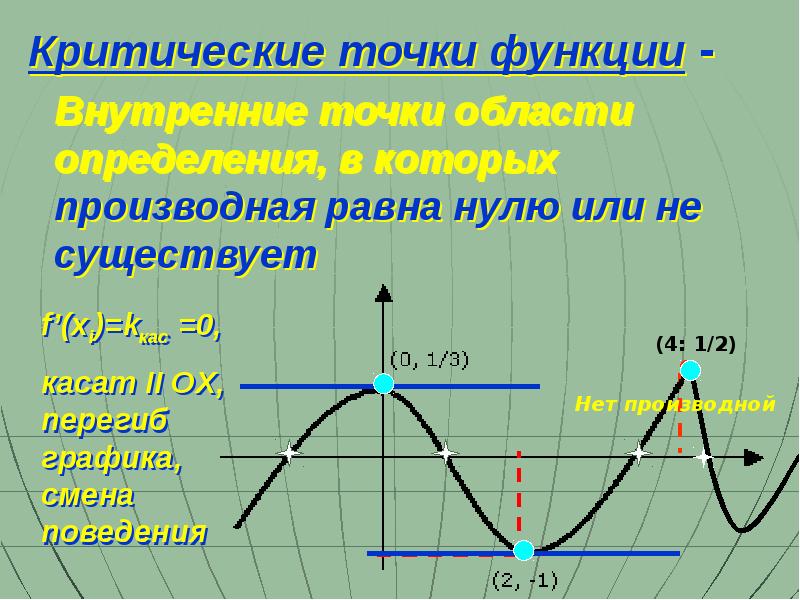
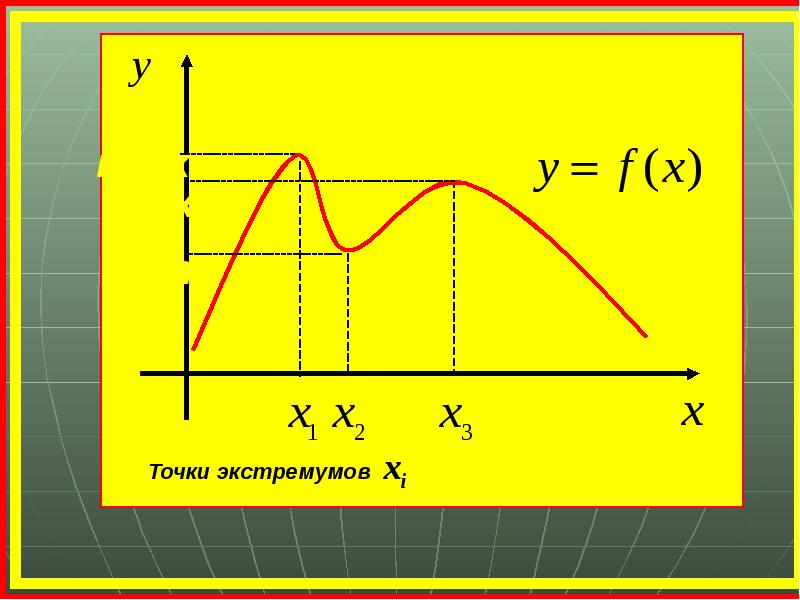
- 15. Внутренние точки области определения, в которых производная равна нулю или не
- 20. Обратите внимание!!! Что происходит с производной при переходе через экстремальную точку?
- 21. Скачать презентацию











Слайды и текст этой презентации
Скачать презентацию на тему Применение производной к исследованию функций можно ниже:
Похожие презентации





























