СЛУ. Теорема Крамера. Метод обратной матрицы презентация
Содержание
- 3. ТЕОРЕМА КРАМЕРА Если главный определитель системы линейных алгебраических уравнений Δ отличен от
- 4. Формулы Крамера где Δj=0 (j=1,…,n) - определители, образованные из главного определителя СЛУ
- 5. Однородные системы ЛУ (ОСЛУ) Система уравнений с нулевыми свободными членами называется
- 6. Критерий существования нетривиального решения однородной системы (ОСЛУ) Теорема. Для того, чтобы
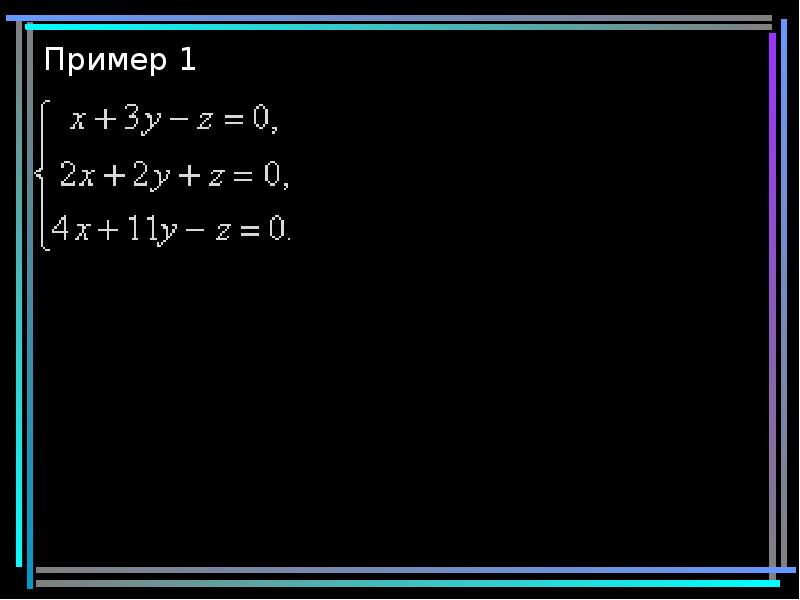
- 7. Пример 1
- 8. Пример 1
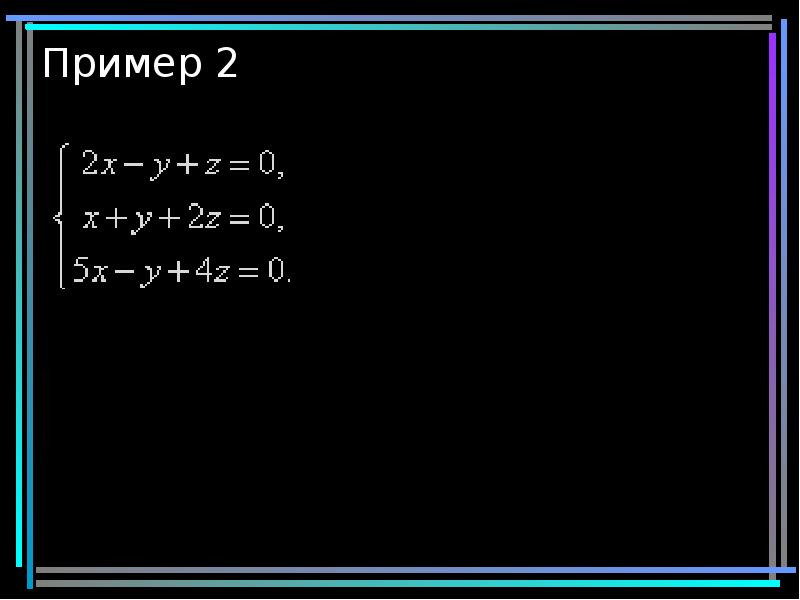
- 9. Пример 2
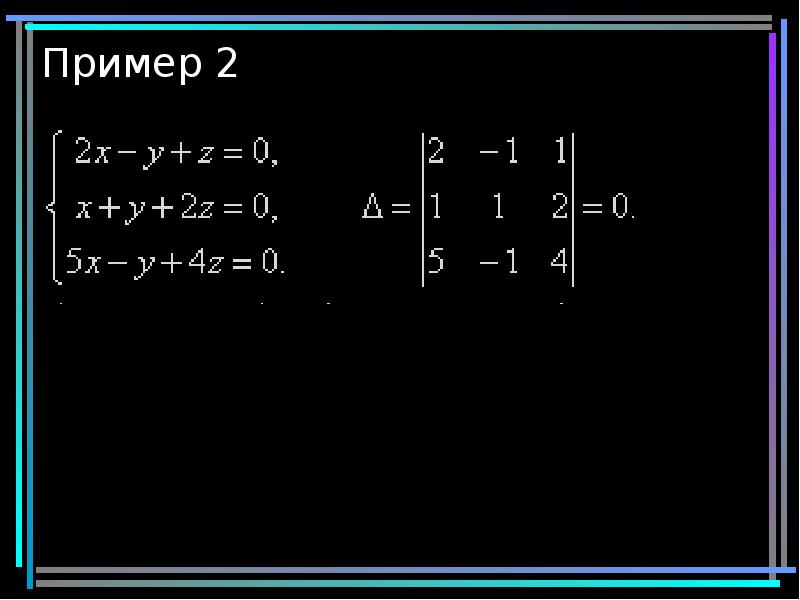
- 10. Пример 2
- 11. Пример 2
- 12. Пример 2
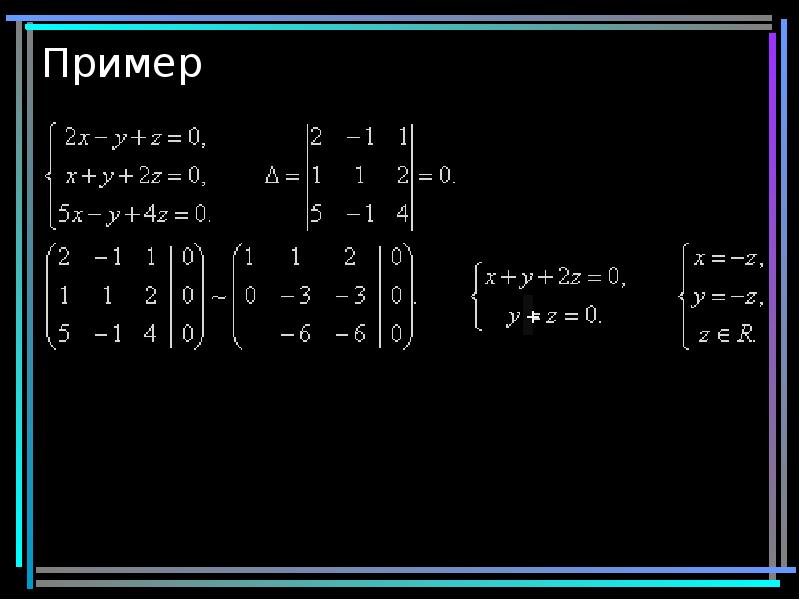
- 13. Пример
- 14. Решение систем линейных уравнений матричным методом или методом обратной матрицы
- 15. Обратная матрица Пусть A — квадратная матрица порядка nхn:
- 16. Пример
- 17. Невырожденная матрица ― квадратная матрица, определитель которой отличен от нуля. В
- 18. Всякая невырожденная матрица A имеет единственную обратную матрицу.
- 19. Свойства обратной матрицы (справедливы для любых невырожденных матриц): (A·B)−1 = B−1·A−1;
- 20. Пусть задана СЛАУ следующего вида:
- 21. Эту систему можно представить в матричном виде: AX = b, где
- 23. Система уравнений называется совместной, если она имеет хотя бы одно решение,
- 24. Порядок операций при вычислении обратной матрицы:
- 26. Матрица, обратная к диагональной матрице — диагональная матрица. Пример –доказать
- 27. Матрица, обратная к треугольной матрице — треугольная матрица
- 30. Найти решение системы уравнений: 3x1-5x2= 22 x1+4x2= 5
- 32. Скачать презентацию

















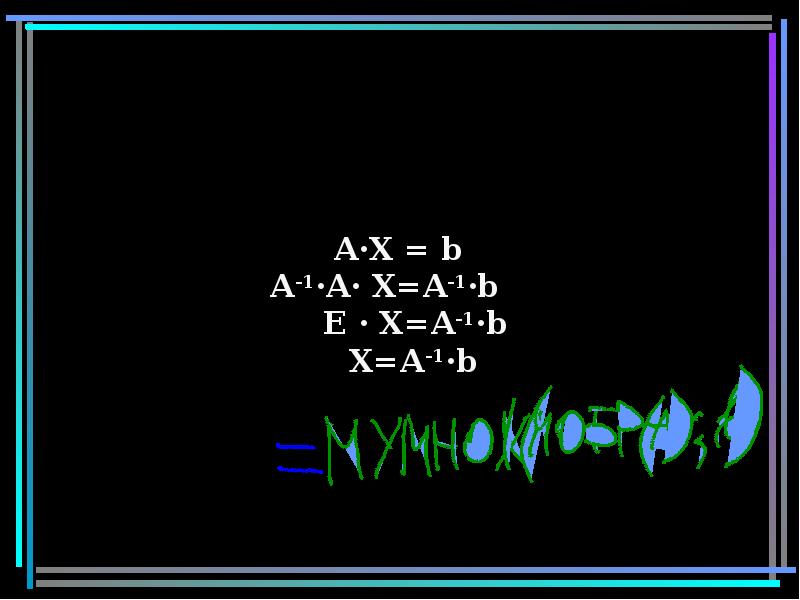









Слайды и текст этой презентации
Скачать презентацию на тему СЛУ. Теорема Крамера. Метод обратной матрицы можно ниже:
Похожие презентации





























