Способы решения уравнения sinX - cosX = 1 презентация

Способы решения уравнения sinX-cosX=1 Работа Кострициной Полины, Косторева Ярослава Гледких Алексея, Плешкова Владислава

Использование формулы понижения степени и двойного угла Cos x/2=0 x/2=п/2+Пn, n принад.Z X=П+2Пn, n принад.Z Ответ: x=П + 2Пn, n принад.Z x=П/2 + 2Пn, n принад.Z

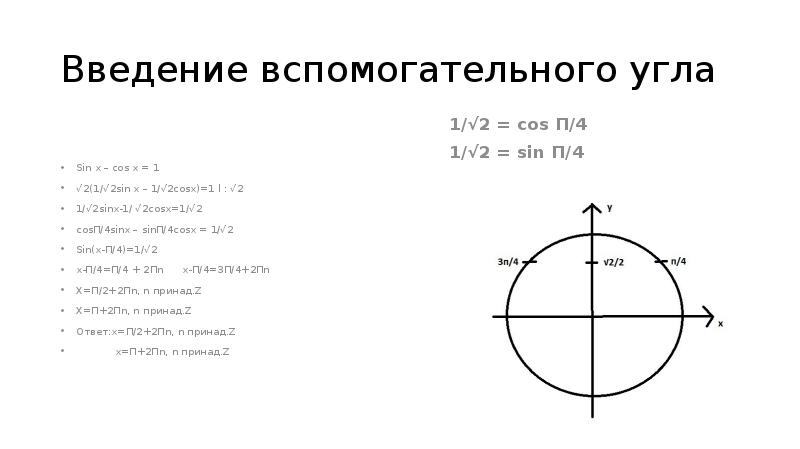
Введение вспомогательного угла Sin x – cos x = 1 √2(1/√2sin x – 1/√2cosx)=1 l : √2 1/√2sinx-1/ √2cosx=1/√2 cosП/4sinx – sinП/4cosx = 1/√2 Sin(x-П/4)=1/√2 x-П/4=П/4 + 2Пn x-П/4=3П/4+2Пn X=П/2+2Пn, n принад.Z X=П+2Пn, n принад.Z Ответ:x=П/2+2Пn, n принад.Z x=П+2Пn, n принад.Z

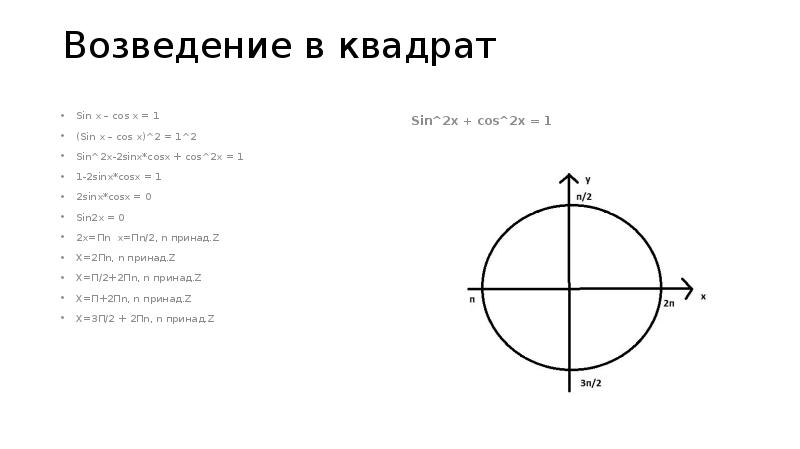
Возведение в квадрат Sin x – cos x = 1 (Sin x – cos x)^2 = 1^2 Sin^2x-2sinx*cosx + cos^2x = 1 1-2sinx*cosx = 1 2sinx*cosx = 0 Sin2x = 0 2x=Пn x=Пn/2, n принад.Z X=2Пn, n принад.Z X=П/2+2Пn, n принад.Z X=П+2Пn, n принад.Z X=3П/2 + 2Пn, n принад.Z

Проверка: sinx-cosx 1)sin2п-cos2п = 1 0-1=1 -1не=1

Формулы универсальной подстановки Sinx = 2tg x/2 / 1+tg^2 x/2 Cosx = 1 – tg^2 x/2 / 1+ tg^2 x/2 2 tg x/2 / 1 + tg^2 x/2 – 1-tg^2 x/2 / 1 + tg^2 x/2 = 1 l* 1 + tg^2 x/2не=0 так как tg 2x/2>=0 2tg x/2 - 1 + tg^2 x/2 = 1 + tg^2 x/2 2tg x/2 = 2 l : 2 tg x/2 = 1 Xне= П+ 2Пn n принад.Z x/2 = П/4 + Пn, n принад.Z Проверим: x = П/2 + 2Пn, n принад.Z sinx - cosx = 1 sinП – cosП = 1 Ответ: 0-(-1) = 1 x = П/2 + 2Пn, n принад.Z 1=1 + x = П + 2Пn, n принад.Z

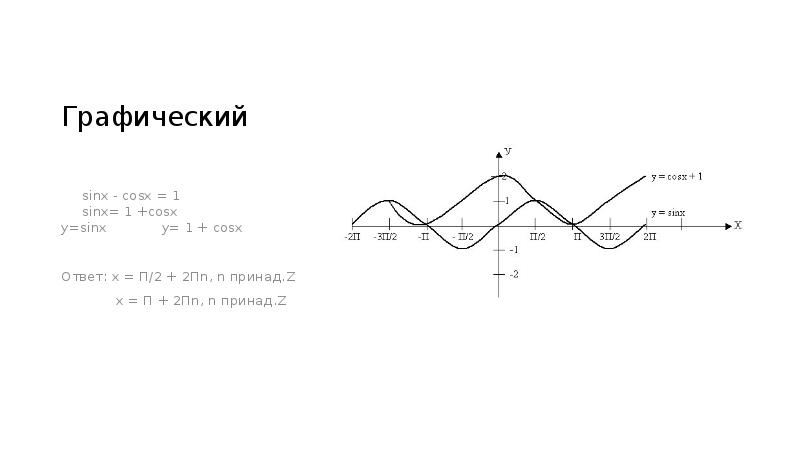
Графический sinx - cosx = 1 sinx= 1 +cosx y=sinx y= 1 + cosx Ответ: x = П/2 + 2Пn, n принад.Z x = П + 2Пn, n принад.Z

Сведение к однородному Cos x/2 = 0 x/2 = П/2 + Пn, n принад.Z X = П + 2Пn, n принад.Z Ответ: x = П/2 + 2Пn, n принад.Z x = П + 2Пn, n принад.Z

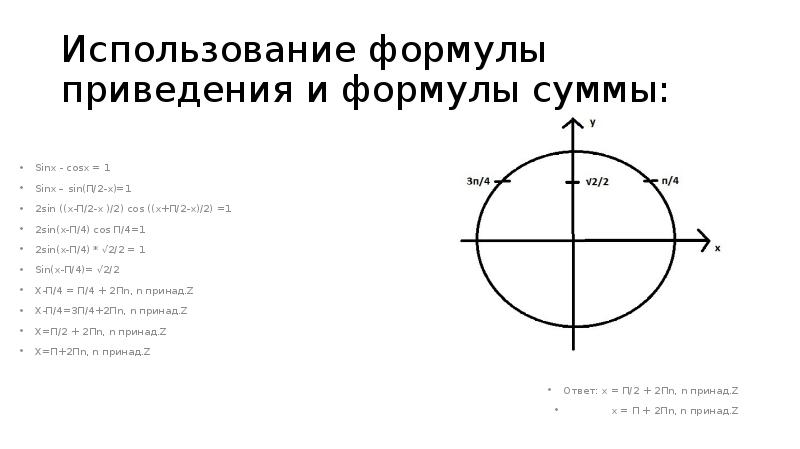
Использование формулы приведения и формулы суммы: Sinx - cosx = 1 Sinx – sin(П/2-x)=1 2sin ((x-П/2-x )/2) cos ((x+П/2-x)/2) =1 2sin(x-П/4) cos П/4=1 2sin(x-П/4) * √2/2 = 1 Sin(x-П/4)= √2/2 X-П/4 = П/4 + 2Пn, n принад.Z X-П/4=3П/4+2Пn, n принад.Z X=П/2 + 2Пn, n принад.Z X=П+2Пn, n принад.Z

СПАСИБО ЗА ВНИМАНИЕ