Презентация, доклад Сравнительный анализ

Лекция 3. Сравнительный анализ

Понятие выборки Генеральная совокупность – это все множество объектов, в отношении которого формулируется исследовательская гипотеза. Это не бесконечное по численности, но, как правило, недоступное для сплошного исследования множество потенциальных участников исследования. Выборка – это ограниченная по численности группа объектов (участников исследования, респондентов), специально отбираемая из генеральной совокупности для изучения ее свойств.

Репрезентативность выборки это представительность или способность выборки представлять изучаемые явления достаточно полно – с точки зрения их изменчивости в генеральной совокупности. Приемы достижения репрезентативности: Простой случайный (рандомизированный) отбор. Стратифицированный случайный отбор (отбор по свойствам генеральной совокупности).

Объем выборки Строгих рекомендаций по предварительному определению требуемого объема выборки не существует. Наиболее общие рекомендации: При разработке диагностической методики – от 200 до 1000-2500 человек. При сравнении двух выборок, общая численность – 50-60 человек. При изучении взаимосвязи – не меньше 30 человек. Чем больше изменчивость свойства, тем больше должен быть объем выборки. Изменчивость можно уменьшить увеличивая однородность выборки, но при этом уменьшаются возможности генерализации выводов.

Зависимые и независимые выборки Зависимые выборки – это те выборки, в которых каждому респонденту одной выборки поставлен в соответствие по определенному критерию респондент другой выборки. Независимые выборки – это те выборки, в которых вероятность отбора любого респондента одной выборки не зависит от отбора любого из респондентов другой выборки.

Выбор критерия для сравнения двух выборок

Критерий t-Стьюдента для независимых выборок Проверяет гипотезу о том, что средние значения двух генеральных совокупностей из которых извлечены независимые выборки, отличаются друг от друга. Исходные предположения: Одна выборка извлекается из одной генеральной совокупности, другая – из другой (значения измеренных признаков гипотетически не должны коррелировать между собой). В обеих выборках распределение приблизительно соответствует нормальному закону. Дисперсии признаков в двух выборках примерно одинаковы.

Структура исходных данных: изучаемый признак(и) измерен у респондентов, каждый из которых принадлежит к одной из сравниваемых выборок. Ограничения: Распределения существенно не отличаются от нормального закона в обеих выборках. При разной численности выборок дисперсии статистически достоверно не различаются (проверяется по критерию F-Фишера или по критерию Ливена.

Формула для подсчетов где, – среднее значение первой выборки - среднее значение второй выборки - стандартное отклонение по первой выборке - стандартное отклонение по второй выборке

Критерий t-Стьюдента для зависимых выборок Проверяет гипотезу о том, что средние значения двух генеральных совокупностей, их которых извлечены сравниваемые зависимые выборки, отличаются друг от друга. Исходные предположения: Каждому представителю одной выборки поставлен в соответствие представитель другой выборки. Данные двух выборок положительно коррелируют. Распределение в обеих выборках соответствует нормальному закону. Структура исходных данных: имеется по два значения изучаемого признака(ов).

U-критерий Манна-Уитни для независимых выборок Показывает насколько совпадают (пересекаются) два ряда значений измеренного признака (ов). Условия для применения: Распределение хотя бы в одной выборке отличается от нормального вида. Небольшой объем выборки (больше 100 человек – используют параметрические критерии, меньше 10 человек – непараметрические, но результаты считаются предварительными). Нет гомогенности дисперсий при сравнении средних значений.

Т-критерий Вилкоксона для зависимых выборок В основе лежит упорядочивание величин разностей (сдвигов) значений признака в каждой паре его измерений. Идея критерия заключается в подсчете вероятности получения минимальной из положительных и отрицательных разностей при условии, что распределение положительных или отрицательных разностей равновероятно и равно

Н-критерий Крускала-Уоллиса для 3 и более независимых выборок Применяется для оценки различий по степени выраженности анализируемого признака одновременно между тремя, четырьмя и более выборками. Позволяет выявить степень изменения признака в выборках, не указывая на направление этих изменений.

Н-критерий Крускала-Уоллиса Условия для применения: Измерение должно быть проведено в шкале порядка, интервалов или отношений. Выборки должны быть независимыми. Допускается разное число респондентов в сопоставляемых выборках. При сопоставлении трех выборок допускается, чтобы в одной из них было n=3, а в двух других n=2. Но в этом случае различия могут быть зафиксированы только на уровне средней значимости.

Критерий Фишера φ (Угловое преобразование Фишера) Критерий φ (фи) предназначен для сопоставления двух рядов выборочных значений по частоте встречаемости какого-либо признака. Этот критерий можно применять на любых выборках – зависимых и независимых. А также можно оценивать частоту встречаемости признака и количественной, и качественной переменной.

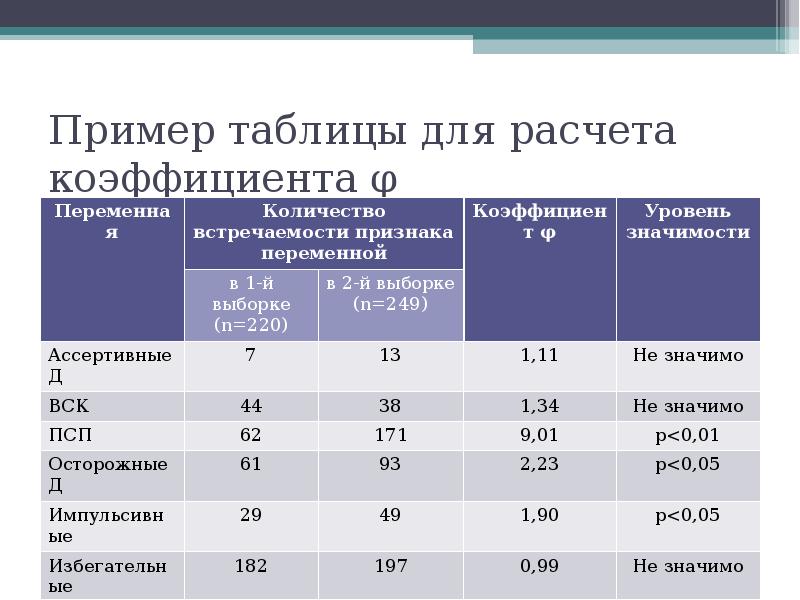
Пример таблицы для расчета коэффициента φ

Критерий Фишера φ Условия для применения: Измерение может быть проведено в любой шкале. Характеристики выборок могут быть любыми. Нижняя граница – в одной из выборок может быть только 2 наблюдения, при этом во второй должно быть не менее 30 наблюдений. Верхняя граница не определена. При малых объемах выборок, нижние границы выборок должны содержать не менее 5 наблюдений каждая.