Статистический анализ зависимостей между гидрологическими переменными (лекция 11) презентация

Лекция 11 Статистический анализ зависимостей между гидрологическими переменными Интервальная оценка и оценка значимости параметров линейной регрессии для двух переменных. Интервальная оценка коэффициента парной корреляции. Коэффициент ранговой корреляции Спирмэна. Интервальная оценка коэффициента регрессии. Интервальная оценка свободного члена (Ахметов С.К.)

Интервальная оценка и оценка значимости параметров линейной регрессии для двух переменных В случае, если r не очень велико и длина выборок не превышает 40 лет, то распределение коэффициентов корреляции хорошо аппроксимируется нормальным законом со среднеквадратическим отклонением σ*r,

Z – преобразование Фишера В случае, если значения r>0.4 и n <40, для построения доверительного можно использовать Z – преобразование Фишера, которое связано с r выражением Z = 0.5 ln[(1+ r)/(1- r)] В отличие от r статистика Z имеет нормальное распределение даже при n небольшом. СКО для Z определяется по формуле

Последовательность построения интервальной оценки r при использовании преобразования Фишера Рассчитывается Z по формуле Z = 0.5 ln[(1+ r)/(1- r)] Рассчитывается СКО Z по формуле 3. Строиться доверительный интервал для Z  Z* - t’1- ασz* ≤ r < Z* + t’1- ασz* 

Проверки значимости линейной зависимости между X и Y Коэффициент корреляции можно использовать для проверки значимости линейной зависимости между X и Y. В этом случае выдвигается нулевая гипотеза, что r=0, т.е. что связь полностью отсутствует. Гипотеза опровергается, если

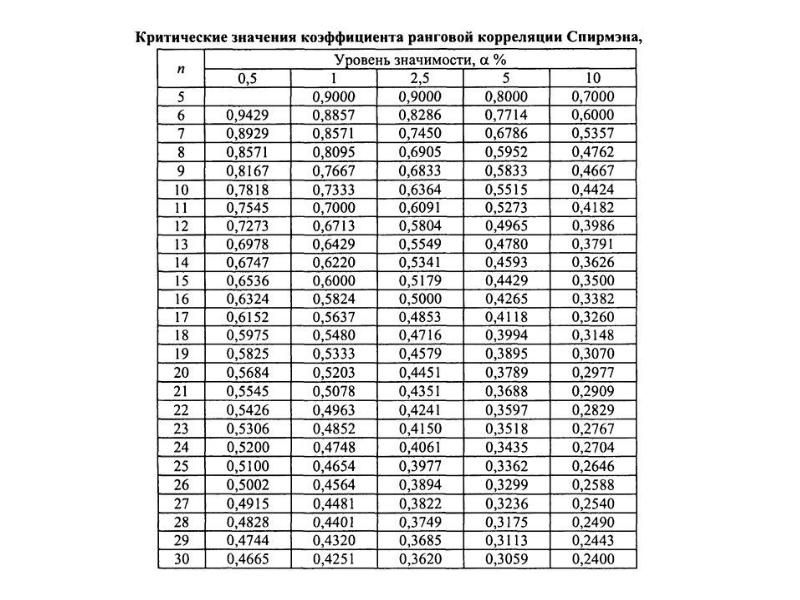
Коэффициент ранговой корреляции Спирмэна Если распределение случайных рядов y1, y2….yn и x1, x2 …xn существенно отличается от нормального распределения, то для оценки степени их взаимосвязанности можно использовать коэффициент ранговой корреляции Спирмэна rs:

Коэффициент ранговой корреляции Спирмэна При n ≥ 30 величина rs√( n-1) достаточно хорошо описывается нормальным распределением. В этом случае нулевая гипотеза (rs=0) отвергается , если выполняется неравенство

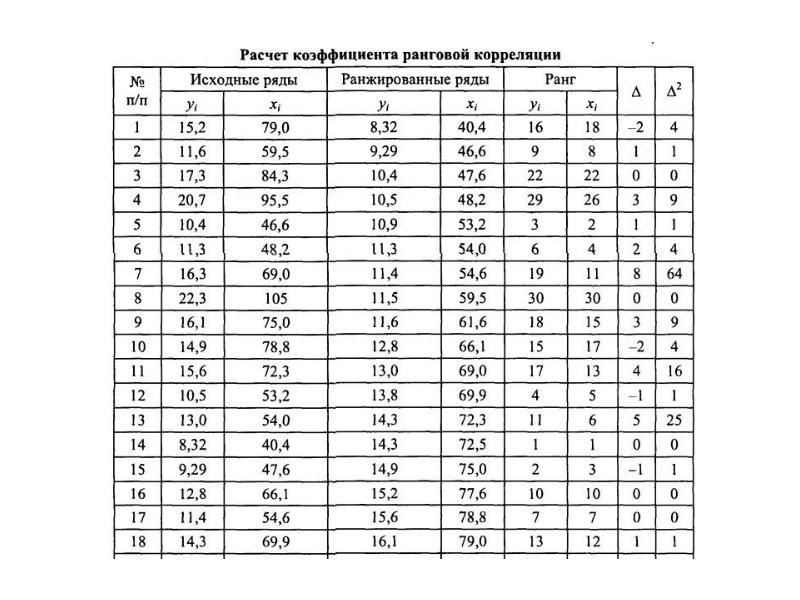
Последовательность расчетов по методу коэффициента ранговой корреляции Спирмэна Ряды yi и xi ранжируются в возрастающем порядке 2. Каждому значению yi и xi в ранжированном ряду присваивается порядковый номер (ранг). Самое маленькое значение случайной величины получает первый ранг и т.д. Каждому значению случайной величины ставится свой ранг 4. Рассчитывается разность рангов yi и xi 5. Рассчитывается квадрат разности рангов ∆2 6. По формуле ниже рассчитывается коэффициент ранговой корреляции По таблице опред-ся критический коэффициент ранговой корреляции

Интервальная оценка коэффициента регрессии Если разброс наблюдений относительно линейной регрессии нормален, то доверительный интервал для коэффициента регрессии имеет вид

Интервальная оценка свободного члена Доверительный интервал для свободного члена имеет вид

F – критерий значимости регрессии Часто для проверки значимости линейной регрессии используется критерий

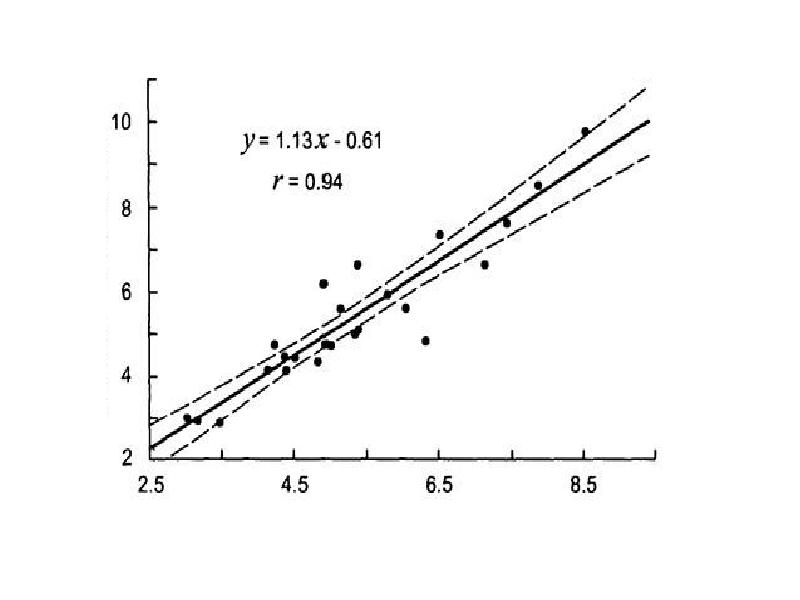
Построение доверительного интервала для уравнения регрессии

СПАСИБО ЗА ВНИМАНИЕ!