Теоремы сложения и умножения вероятностей. (Лекция 3) презентация
Содержание
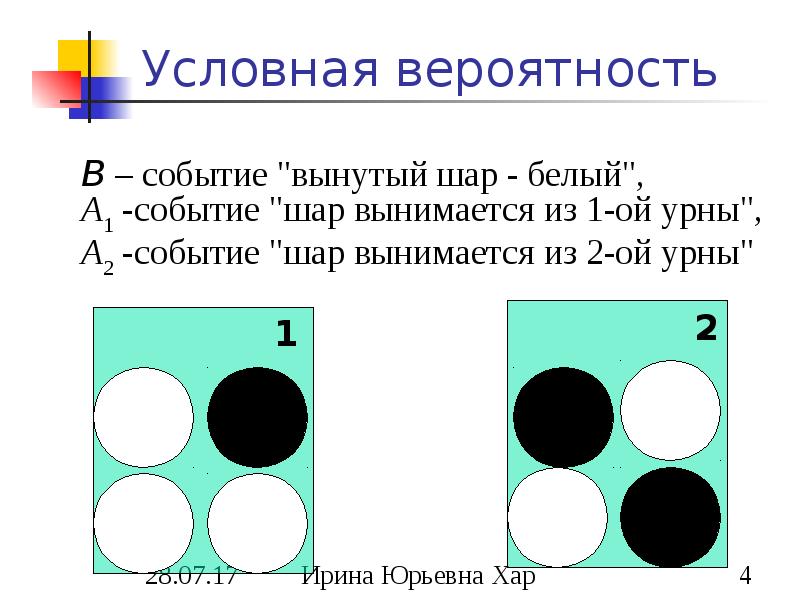
- 2. 1. УСЛОВНАЯ ВЕРОЯТНОСТЬ
- 3. Условная вероятность Вероятность события А при условии, что событие В с
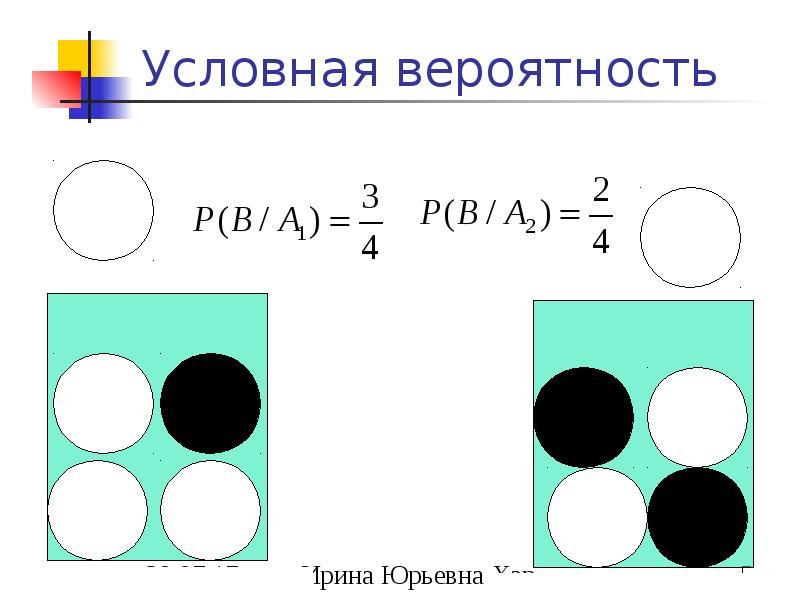
- 4. Условная вероятность
- 5. Условная вероятность
- 6. События А и В называются независимыми если осуществление одного не влияет
- 7. 2. ПРОИЗВЕДЕНИЕ ВЕРОЯТНОСТЕЙ
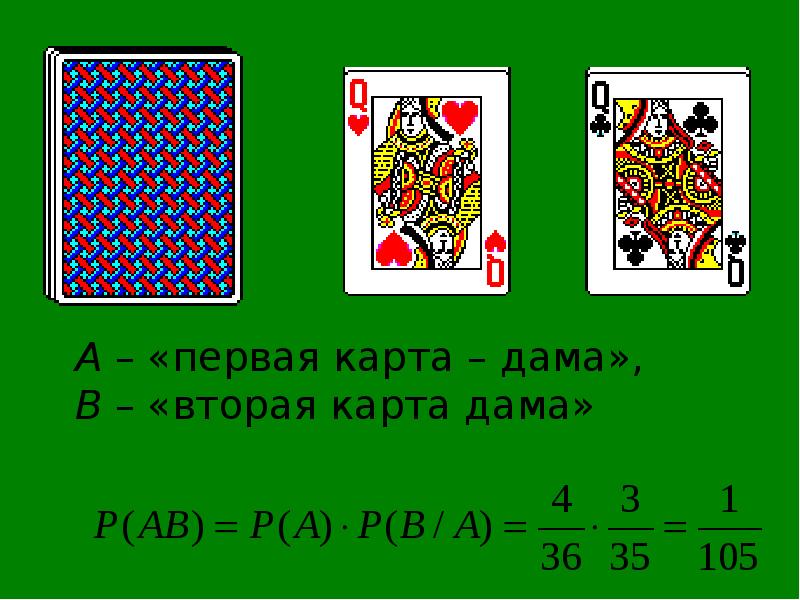
- 8. ТЕОРЕМА 1 Вероятность совместного появления двух событий равна произведению вероятности одного
- 10. ТЕОРЕМА 2 Вероятность совместного появления двух независимых событий равна произведению их
- 11. ТЕОРЕМА 2
- 12. ТЕОРЕМА 3 Если для двух событий выполняется равенство то эти события
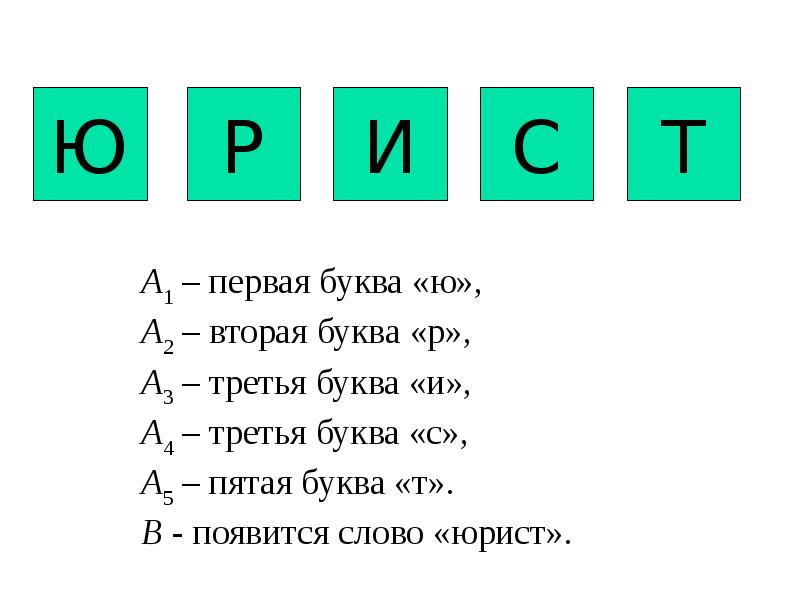
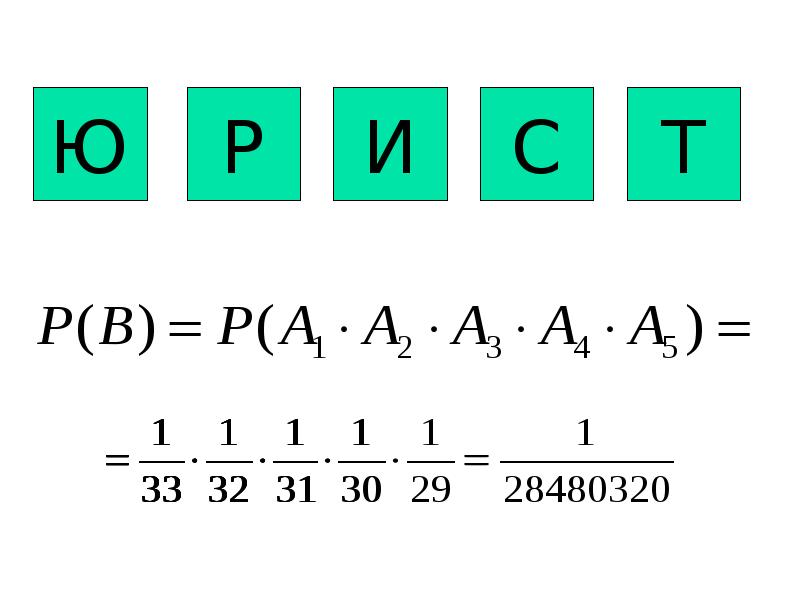
- 13. ТЕОРЕМА 4 Вероятность совместного наступления конечного числа событий равна произведению вероятности
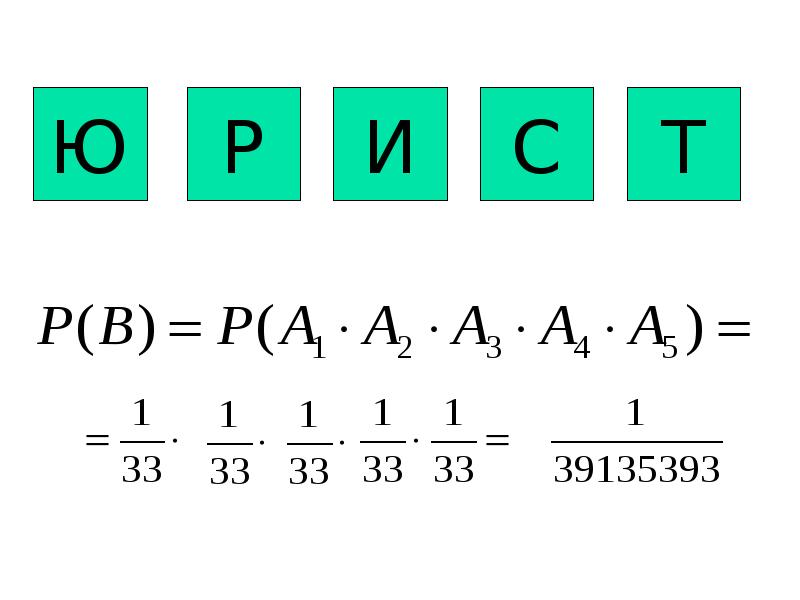
- 16. ТЕОРЕМА 5 Вероятность совместного появления нескольких событий, независимых в совокупности, равна
- 18. 3. СУММА ВЕРОЯТНОСТЕЙ
- 19. ТЕОРЕМА 6 Вероятность появления одного из двух несовместных событий, равна сумме
- 20. 25 ЧЕЛОВЕК ИМЕЮТ СЛЕДУЮЩИЕ ОЦЕНКИ
- 23. ТЕОРЕМА 7 Вероятность появления одного из нескольких попарно несовместных событий равна
- 24. СЛЕДСТВИЕ Сумма вероятностей попарно несовместных событий, образующих полную группу, равна 1:
- 27. ТЕОРЕМА 8 Вероятность появления хотя бы одного из двух совместных событий
- 29. СЛЕДСТВИЕ В случае трех совместных событий вероятность их суммы вычисляется по
- 30. ТЕОРЕМА 9 Вероятность появления хотя бы одного из событий, независимых в
- 32. 3. Формула полной вероятности. Формула Байеса
- 33. ТЕОРЕМА 10 Вероятность события А, которое может наступить только при условии
- 36. Алгоритм применения ф.Байеса 1. Выдвигают предположения – гипотезы В1, В2,...,Вn. Данные гипотезы
- 37. Алгоритм применения ф.Байеса 2. Устанавливают доопытные (априорные) вероятности данных гипотез: из интуитивных
- 38. Алгоритм применения ф.Байеса 3. Проводят эксперимент, в результате которого происходит событие А.
- 39. Алгоритм применения ф.Байеса где Р(А) определяется по формуле полной вероятности.
- 44. Скачать презентацию





































Слайды и текст этой презентации
Скачать презентацию на тему Теоремы сложения и умножения вероятностей. (Лекция 3) можно ниже:
Похожие презентации





























