Теория массового обслуживания презентация
Содержание
- 2. Теория массового обслуживания начала развиваться в начале XX столетия. Основоположником
- 3. Значительный вклад в создание и разработку общей теории массового обслуживания внес
- 4. В зарубежной литературе теория массового обслуживания известна под названием «Теория очередей».
- 5. Для достижения этой цели ставятся задачи теории массового обслуживания, состоящие в
- 6. В сфере производства и обслуживания примерами СМО могут служить:
- 7. Такие системы как компьютерные сети, системы сбора, хранения и обработки информации,
- 8. Случайные процессы и потоки событий В качестве аппарата теории систем массового
- 9. Потоком называется последовательность событий, наступающих одно за другим, в общем случае,
- 11. Теорема 8.1. Если постоянная интенсивность потока ʎ известна, то вероятность появления
- 12. Пример 8.1. На автоматическую телефонную станцию поступает простейший поток вызовов с
- 13. Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (или требований),
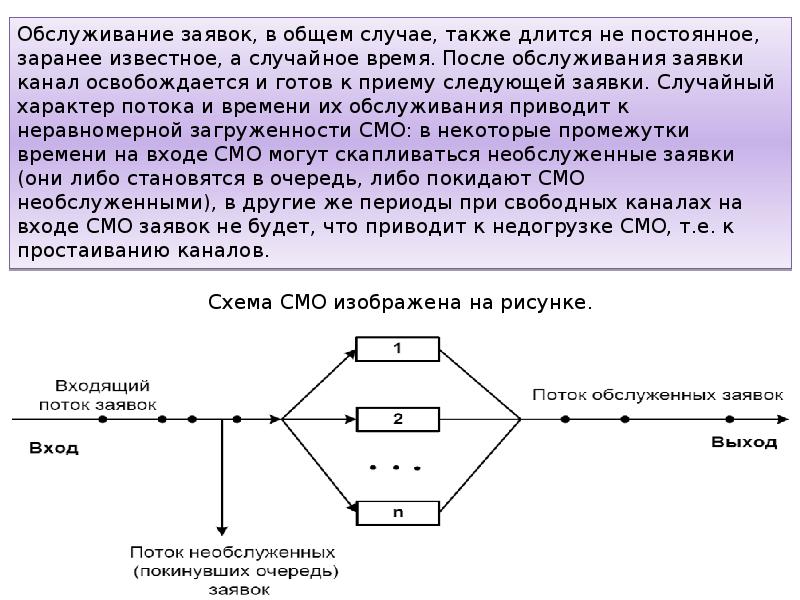
- 14. Обслуживание заявок, в общем случае, также длится не постоянное, заранее известное,
- 15. Таким образом, во всякой СМО можно выделить следующие основные элементы: 1)
- 16. В качестве характеристик эффективности функционирования СМО можно выбрать три основные группы
- 17. По числу каналов Одноканальные
- 18. По дисциплине обслуживания СМО подразделяют на три класса
- 20. ОДНОКАНАЛЬНЫЕ СМО
- 21. Одноканальная СМО с отказами
- 22. Для составления матрицы перехода мы должны вычислить
- 28. Одноканальная СМО с ожиданием и ограниченной очередью
- 29. Интенсивность потока обслуживаний автомобилей: Приведенная интенсивность потока автомобилей определяется
- 30. Среднее число автомобилей, находящихся на обслуживании и в очереди (т.е. в
- 31. Одноканальная СМО с ожиданием и неограниченной очередью
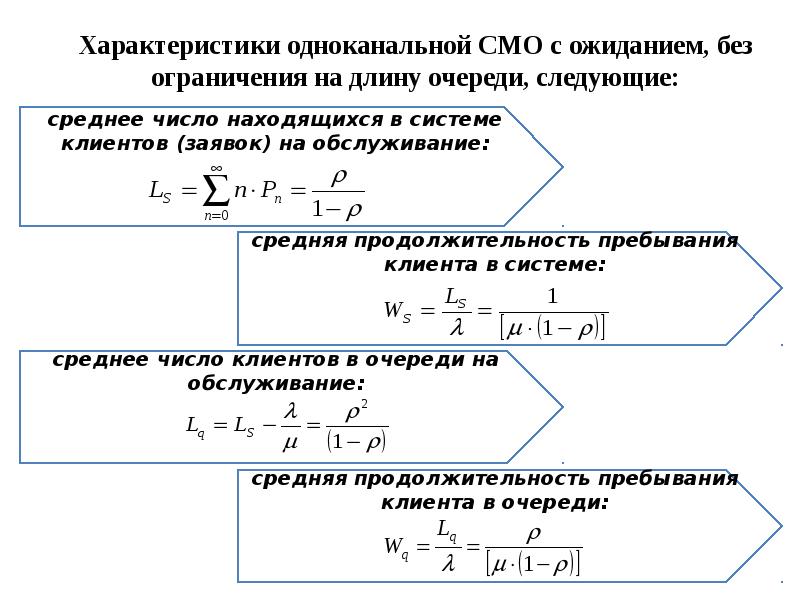
- 32. Характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди, следующие:
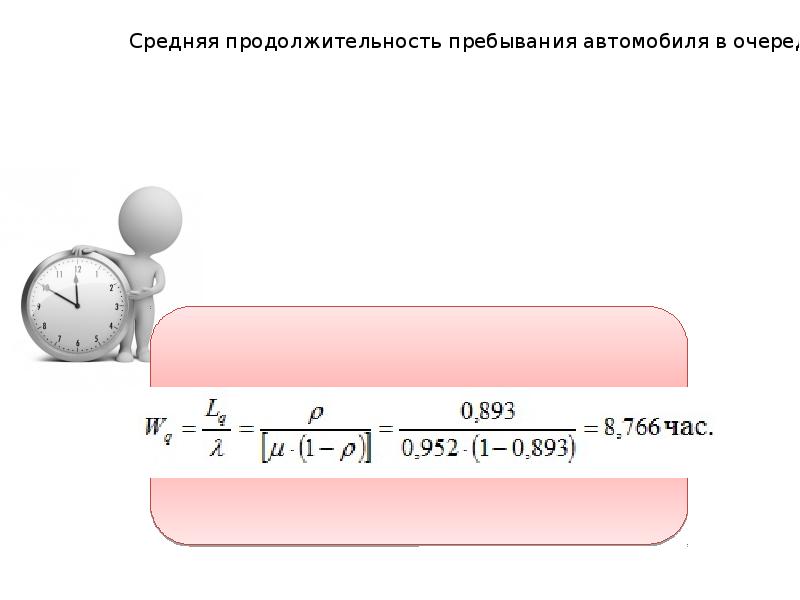
- 33. Пример 9.3 Пусть рассматриваемое зона таможенного контроля в пункте пропуска располагает
- 34. Решение Параметр потока обслуживания и приведенная интенсивность потока автомобилей ρ определены
- 41. В подавляющем большинстве случаев на практике система массового обслуживания является многоканальными,
- 42. Стационарное решение системы имеет вид: где
- 44. Пример 9.4. Пусть n-канальная СМО представляет собой вычислительный центр (ВЦ) с
- 46. Таким образом, при установившемся режиме работы СМО в среднем будет занято
- 51. Скачать презентацию














































Слайды и текст этой презентации
Похожие презентации





























