Теория вероятностей, математическая статистика и случанйные процессы презентация

ШАЛАЕВ Ю.Н. доцент каф. ИПС, АВТФ ТЕОРИЯ ВЕРОЯТНОСТЕЙ, МАТЕМАТИЧЕСКАЯ СТАТИСТИКА И СЛУЧАНЙНЫЕ ПРОЦЕССЫ Лекции- 26 часов Практические занятия- 26 часов Экзамен, зачет.

Литература 1 .Гмурман В.Е. Курс теории вероятностей. М.: В.Ш. 1977,1999. 2. Вентцель Е. С. Теория вероятностей М.: Наука, 1979,2000. 3. Чистяков В.П. Курс теории вероятностей. М.:1987. Свешников А.А. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. М.: Наука, 1965.

Пространство элементарных событий Ω Пространством элементарных событий Ω называется множество элементарных событий ωi , удовлетворяющих данному эксперименту: Ω={ω1 , ω2, …, ωn }.

Случайные события Случайным событием или просто событием называется подмножество А множества Ω: A  Ω. А={ω1, ω2,…,ωm}, где m-число элементарных событий случайного события А. Для дискретного Ω число случайных событий N=2n.

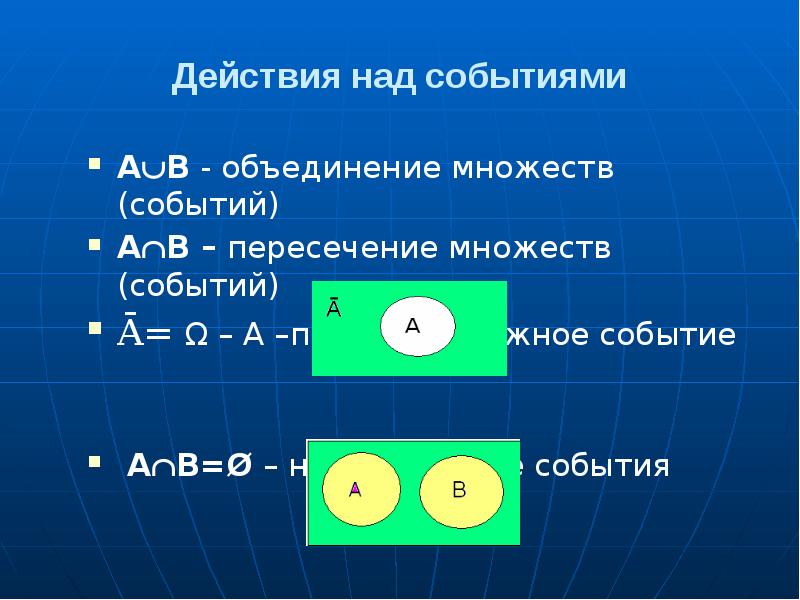
Действия над событиями AB - объединение множеств (событий) AB – пересечение множеств (событий) Ā= Ω – А –противоположное событие AB=Ø – несовместные события

Комбинаторика Основное правило комбинаторики: пусть требуется совершить одно за другим К действий и первое действие можно осуществить n1 способами, второе n2 и так до К действия, которое можно осуществить nk способами, то все К действий можно осуществить N=n1·n2···nk способами.

Сочетания: Сочетания: Перестановки: Размещения: Комбинации с возвращением:

Вероятность Аксиоматическое определение вероятности: Вероятность на пространстве элементарных событий Ω называется функция Р(А), обладающая свойствами: Р(Ω)=1; 0Р(А)1; Р(АВ)=Р(А)+Р(В), АВ=Ø

Классическая вероятность: Р(А)=m/n, n-число элементарных событий для Ω; m-число элементарных событий для А. Классическая вероятность: Р(А)=m/n, n-число элементарных событий для Ω; m-число элементарных событий для А. Геометрическая вероятность: Р(А)=LA/LΩ; Р(А)=SA/SΩ; Р(А)=VA/VΩ, где L-длина, S-площадь, V-объем. Статистическая вероятность: Р(А)=limnA/n. n-∞

Вероятность суммы вероятность суммы для совместных событий А и В определяется по соотношению Р(А U В) = Р(А) + Р(В) – Р(А ∩ В); Вероятность противоположного события Р(Ā)=1-Р(А)

Условная вероятность Условная вероятность для зависимых событий определяется по соотношению Р(А/В) = Р(А ∩ В) / Р(В). События А и В независимы, если условная вероятность равна своей безусловной вероятности Р(А/В) = Р(А);

Вероятность произведения Вероятность произведения двух событий равна произведению вероятностей одного из этих событий на условную вероятность другого при условии, что первое произошло: Р(АВ)=Р(А)·Р(В/А); Для трех событий: Р(АВС)=Р(А)·Р(В/А)·Р(С/АВ); для независимых событий вероятность произведения равна произведению вероятностей Р(А ∩ В) = Р(А) Р(В); Вероятность произведения коммутативна: Р(АВ)=Р(А)·Р(В/А); Р(АВ)=Р(В)·Р(А/В).

Формула полной вероятности А-произвольное событие; События Н1, Н2,…Нn попарно несовместны, называются гипотезами и образуют полную группу событий, при этом Р(Нi)>0,

Формула Байеса Это вероятность наступления К гипотезы при условии, что событие А произошло.

Испытания Бернулли Производится последовательность независимых испытаний, в каждом из которых с постоянной вероятностью Р происходит событие А (успех) и событие Ā с вероятностью q=1-p. Необходимо определить вероятность появления события А в этой в этой серии ровно m раз:

Случайная величина Случайная величина ξ это действительная функция ξ= ξ (ω), ωΩ, определенная на пространстве элементарных событий. Т.е. случайная величина-это функция; аргумент у которой, элементарное событие; значение-число. Случайные события (А,В,…) качественные характеристики случайных явлений. Случайная величина дает количественную характеристику явлений.

Случайная величина дискретного типа Закон задается в виде ряда распределения-это совокупность пар чисел (xk,Pk), где xk-значения, которые принимает случайная величина ξ= xk; Pk-вероятность, которую принимает это значение xk: Pk=P(ξ= xk)>0:

Функция распределения F(x)=P(ξ<x) Это вероятность того, что случайная величина принимает значение расположенное левее точки х. Функция распределения неслучайная функция; аргумент-вещественное х; значение-число.

Свойства функции распределения F(-∞)=0; F(∞)=1; F(x)-неубывающая функция; х1<х2, F(x1)F(x2) F(x)-непрерывная функция; limF(x)=F(x0); x→x0-0; Вероятность попадания случайной величины на заданный интервал [а,в) равно приращению функции распределения на этом интервале: P(аξ<в)= F(в) – F(а)

Случайная величина непрерывного типа f(x) – плотность распределения вероятностей случайной величины ξ.

Плотность вероятностей Плотность распределения вероятностей случайной величины ξ, называется предел отклонения вероятности попадания ξ на малый интервал к длине этого интервала: Если этот предел существует, то он равен производной от функции распределения

Свойства плотности вероятностей График плотности вероятностей f(x) – кривая распределения вероятностей; Плотность вероятностей неотрицательная функция: f(x)  0; Плотность вероятностей нормирована на единицу: Вероятность попадания на интервал [а,в):

Числовые характеристики случайных величин Математическое ожидание – это число, которое характеризует среднее значение случайной величины: для дискретной ξ Для непрерывной ξ:

Свойства математического ожилания 1 Математическое ожидание постоянной величины С равно самой постоянной величине: МС=С; 2 Постоянную величину можно выносить за оператор математического ожидания: МСξ=СМξ; 3 Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих величин: М(ξ + η)=Мξ + Мη : 4 Математическое ожидание произведения независимых случайных величин равно произведению математическое ожиданий этих величин: Мξη=Мξ*Мη.

Дисперсия случайной величины Дисперсией случайной величины ξ называется число Dξ=М(ξ – Мξ)2, Которое является мерой рассеяния случайной значений величины около ее математического ожидания. После преобразования правой части получим второе соотношение для дисперсии: Dξ=Mξ2 – (Mξ)2.

Для дискретной ξ: Для непрерывной ξ:

Свойства дисперсии 1 Дисперсия положительная величина Dξ0; 2 Дисперсия постоянной величины равна нулю: DC=0; 3 Константу можно выносить за оператор дисперсии в квадрате DCξ=C2Dξ;

4 Дисперсия суммы и разности независимых случайных величин равна сумме дисперсий этих величин : D(ξ+η)=Dξ+Dη; D(ξ-η)=Dξ+Dη; 5 Среднее квадратическое отклонение: 6 Дисперсия показывает средний квадрат разброса случайной величины относительно центра (математического ожидания).

Моменты Начальный момент К порядка: k=Mξk, 1=Mξ; Для дискретной ξ: Для непрерывной ξ:

Центральный момент К порядка: μк=М(ξ-Мξ)к, μ1=0, μ2=Dξ; Для дискретной ξ: Для непрерывной ξ:

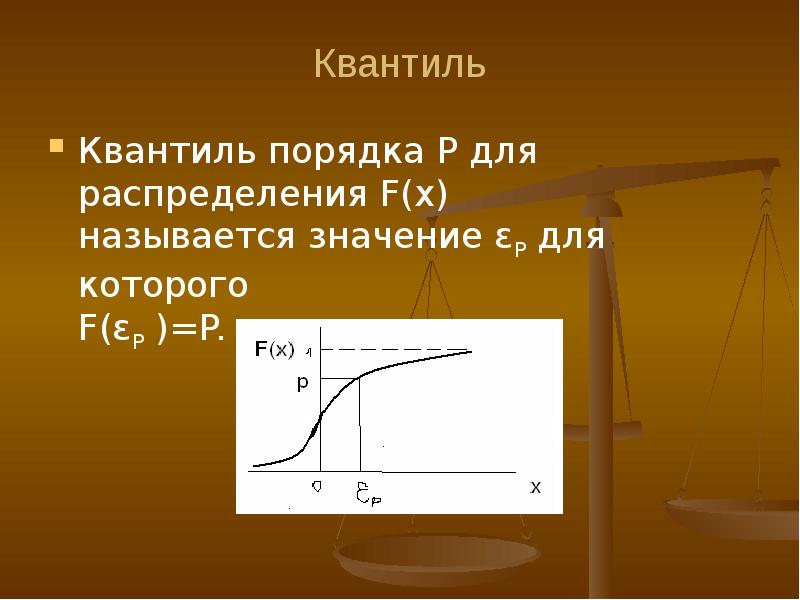
Квантиль Квантиль порядка Р для распределения F(x) называется значение εР для которого F(εР )=P.

Типовые законы распределения случайных величин Биномиальный закон: Проводится серия из “n”однородных и независимых опытов. А – событие успеха, которое может появится в опыте. Случайная величина ξ – число успехов появления события А в серии из “n” опытов. ξ – дискретная случайная величина и ее значения целые числа: ξ=k; k=0,1,2,…, “n” .

Целочисленная случайная величина ξ подчинена биномиальному закону, если вероятности ряда распределения вычисляются по формуле Бернулли: Математическое ожидание: Мξ=np; Дисперсия: D ξ=npq.

Закон Пуассона ξ – дискретная случайная величина, которая принимает целые неотрицательные значения: k=0,1,2,…,k,…, последовательность этих значений не ограничена n→∞, p→0 так, что np=const. Случайная величина ξ подчинена закону Пуассона, если вероятности ряда распределения вычисляются по формуле Пуассона : Математическое ожидание Mξ=a; Дисперсия Dξ=a.

Равномерное распределение Непрерывная случайная величина ξ распределена по равномерному закону, если плотность распределения имеет вид: Равномерное распределение применяется при определении ошибок вычислений (измерений). Датчик случайных чисел в ЭВМ.

Функция распределения Математическое ожидание: Мξ=(в+а)/2; Дисперсия: Dξ=(b-a)2/12.

Закон экспоненциального распределения Непрерывная случайная величина ξ распределена по экспоненциальному закону, если плотность вероятностей задана формулой: Применяется при расчете надежности различных технических систем.

Функция распределения Математическое ожидание: Мξ=1/λ; Дисперсия: Dξ=1/λ2.

Закон нормального распределения (закон Гаусса) Плотность вероятностей: Функция распределения: Математическое ожидание: Мξ=а; Дисперсия: Dξ=σ2.

Интеграл вероятностей Интеграл вероятностей есть функция распределения Гауссовской случайной величины Z: MZ=0; DZ=1; F(-∞)=0; F(0)=0.5; F(∞)=1; F(-z)=1 – F(z)

Локальная теорема Муавра-Лапласа При неограниченном увеличении числа испытаний “n” формула Бернулли сводится к формуле Гаусса: Формула справедлива для всех 0<р<1 и 0kn.

Интегральная теорема Муавра-Лапласа При неограниченном увеличении числа испытаний “n” вероятность попадания случайной на заданный интервал (a,b] равна где F(z) – интеграл вероятностей.

Системы случайных величин Совокупность нескольких случайных величин, рассматриваемых совместно называется системой случайных величин: {ξ1 ,ξ 2 ,ξ 3, ξn}. Система двух случайных величин {ξ,η} изображается на плоскости в виде вектора; каждой точки соответствует единственный вектор

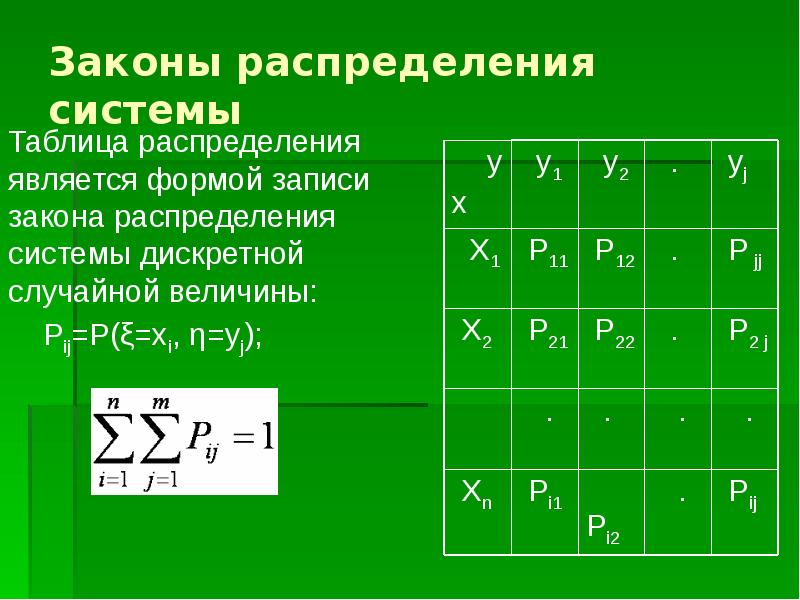
Законы распределения системы Таблица распределения является формой записи закона распределения системы дискретной случайной величины: Pij=P(ξ=xi, η=yj);

Функция распределения системы F(x,y)=P(ξ<x, η<y); Для непрерывной системы случайных величин: f(x,y) – плотность распределения системы случайных величин.

Плотность системы случайных величин Свойства плотности вероятностей системы 1 Плотность системы неотрицательная функция f(x,y)0; 2 Плотность системы нормирована на единицу:

Вероятность попадания системы в область D:

Дисперсия системы Дисперсия системы определяется по законам отдельных составляющих системы: Среднее квадратическое отклонение характеризует рассеивание системы относительно центра (математического ожидания).

Корреляционный момент Корреляционный момент есть математическое ожидание центрированной системы: Для дискретной системы:

Для непрерывной системы: х,у – возможные значения ξ, η; f(x,y) – плотность вероятностей системы. Геометрически Кξη показывает величину отклонения системы от центра. Если Кξη ≠0, то система коррелированна. Если Кξη =0, то система не коррелированна. Из независимости системы вытекает некоррелированность, обратное может быть и неверно.

Свойства корреляционного момента Корреляционный момент симметричен: Кξη = К ηξ; Кξξ = Dξ; Кξξ = M(x-Mξ)(x-Mξ)=Dξ; Kηη= Dη; Kηη= M(y-Mη)(y-Mη)=Dη; Совокупность всех корреляционных моментов, расположенных в квадратной таблице называется корреляционной матрицей системы:

Коэффициент корреляции Наличие размерности у корреляционного момента вызывает неудобства, поэтому вместо корреляционного момента используют коэффициент корреляции:

Коэффициент корреляции обладает свойствами корреляционного момента: показывает меру линейной связи между случайными величинами: rξη = 0, если ξ,η некоррелированные случайные величины; коэффициент корреляции системы симметричен: rξη = rηξ; / rξη /1; (1 – максимальное значение); Совокупность всех коэффициентов корреляции в виде таблице образуют нормированную корреляционную матрицу системы:

Условное математическое ожидание; линейная регрессия Для дискретной ξ: Для непрерывной ξ : Функция регрессии показывает среднее значение η на ξ. С помощью регрессии осуществляется наилучший прогноз η по ξ.

В практике функция регрессии относится к линейной: φ(х)=β0 + β1х; β0, β1 – параметры – коэффициенты регрессии. Коэффициенты регрессии подбирают так, чтобы обеспечить минимум среднего разброса η относительно прямой регрессии (метод наименьших квадратов): вводится уклонение η относительно прямой регрессии: Δ = (у – (β0 + β1х)): находим дисперсию: Δ2(β0, β1) = М(у – (β0 + β1х)) 2 min→ β0, β1 : после преобразования получим: φ(х)=β0 + β1х = Мη + rξη∙ση/σξ∙(x - Mξ).