Векторный анализ. Лекция 4 презентация

Векторный анализ Лекция 4

§4 Поверхности второго порядка §4 Поверхности второго порядка Поверхности второго порядка описываются уравнениями второго порядка относительно переменных x, y, z. Среди поверхностей второго порядка выделим цилиндрические поверхности.

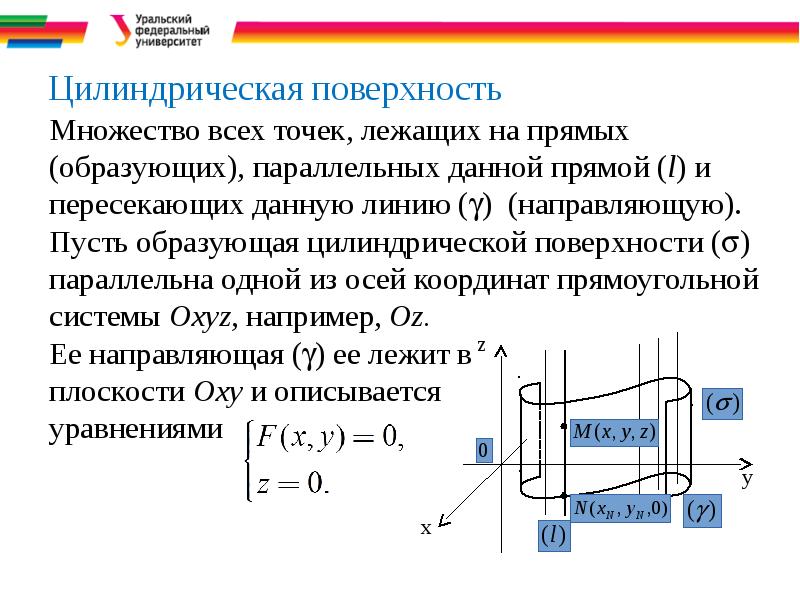
Цилиндрическая поверхность Множество всех точек, лежащих на прямых (образующих), параллельных данной прямой (l) и пересекающих данную линию () (направляющую). Пусть образующая цилиндрической поверхности () параллельна одной из осей координат прямоугольной системы Охуz, например, Oz. Ее направляющая () ее лежит в плоскости Оху и описывается уравнениями

Требуется составить уравнение этой цилиндрической поверхности Точка , где (l) – одна из образующих цилиндрической поверхности (), которая пересекает направляющую () в точке . Т.к. точка N (), то . (*) Точки М и N принадлежат одной и той же прямой (l), параллельной оси Oz, и, следовательно, .

Подставив в равенство (*) вместо хN и yN соответственно х и у, получим равенство F(x,y)=0, которое является уравнением цилиндрической поверхности (). Итак, F(x,y)=0 есть уравнение цилиндрической поверхности с образующими, параллельными оси Oz, и направляющей, расположенной в плоскости Оху.

Замечания Уравнение цилиндрической поверхности, подобной рассмотренной, совпадает с уравнением ее направляющей, расположенной в одной из координатных плоскостей прямоугольной системы Охуz. 2. Уравнение не содержит одной переменной, одноименной с осью, параллельной образующей цилиндрической поверхности.

Пример. - уравнение цилиндрической поверхности с образующей, параллельной оси Oz (в уравнении отсутствует переменная z), с направляющей, расположенной в плоскости Оху и представляющей параболу с тем же самым уравнением.

Поверхности второго порядка Общее уравнение поверхности 2-го порядка имеет вид: где .

Поверхности второго порядка Теорема. Общее уравнение поверхности 2-го порядка с помощью симметрии относительно плоскости, поворота оси и параллельного переноса прямоугольной системы координат может быть приведено к одному из следующих канонических уравнений:

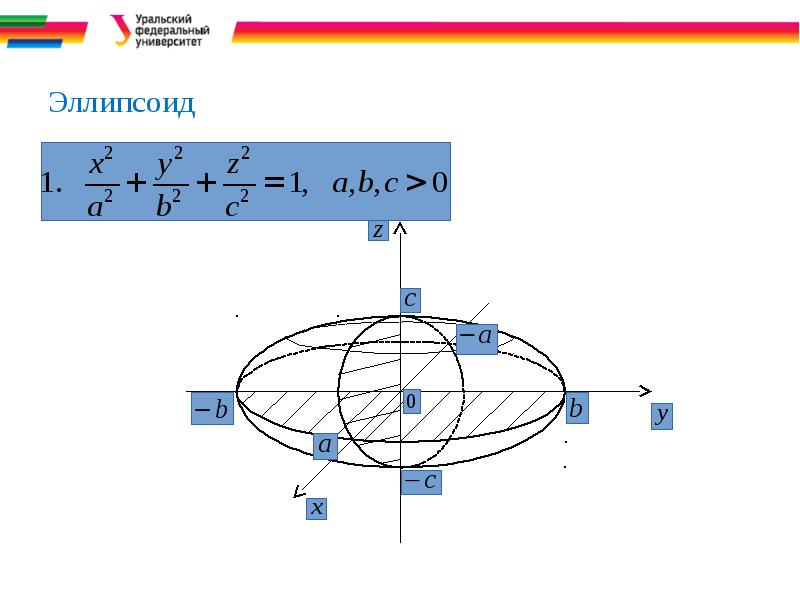
Эллипсоид

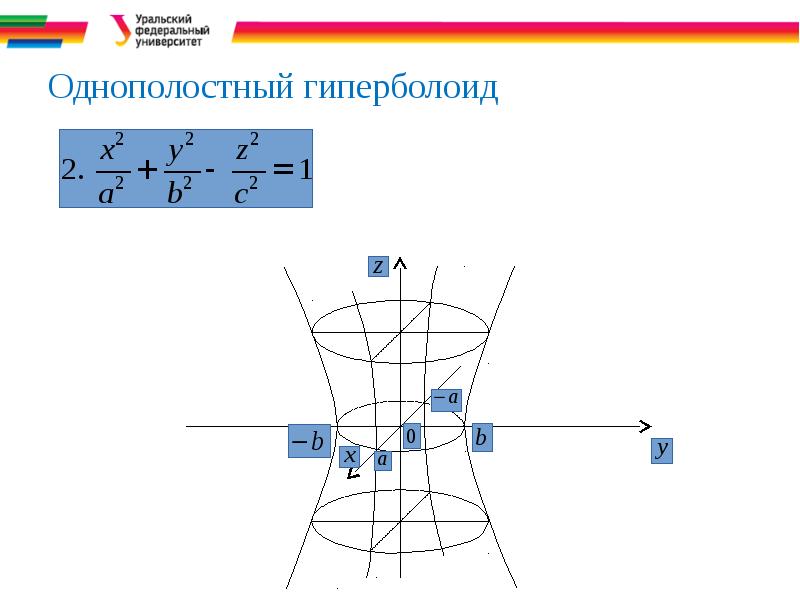
Однополостный гиперболоид

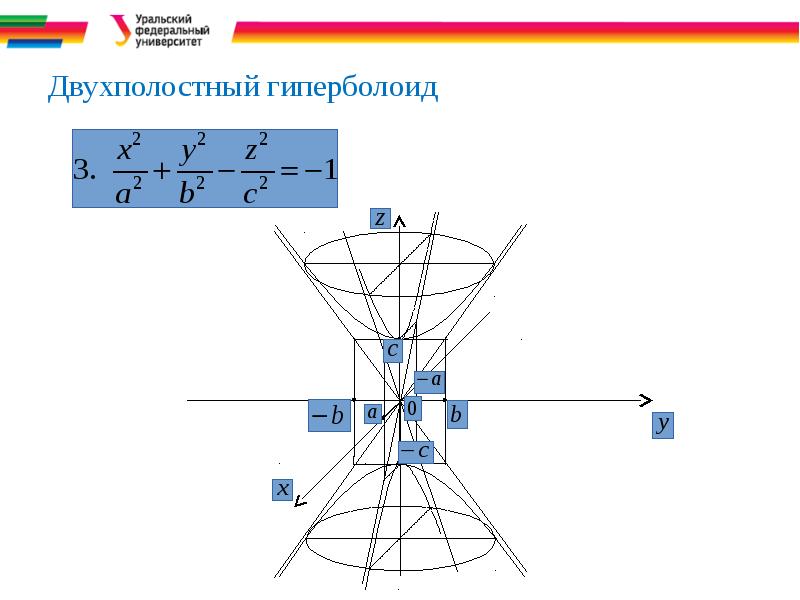
Двухполостный гиперболоид

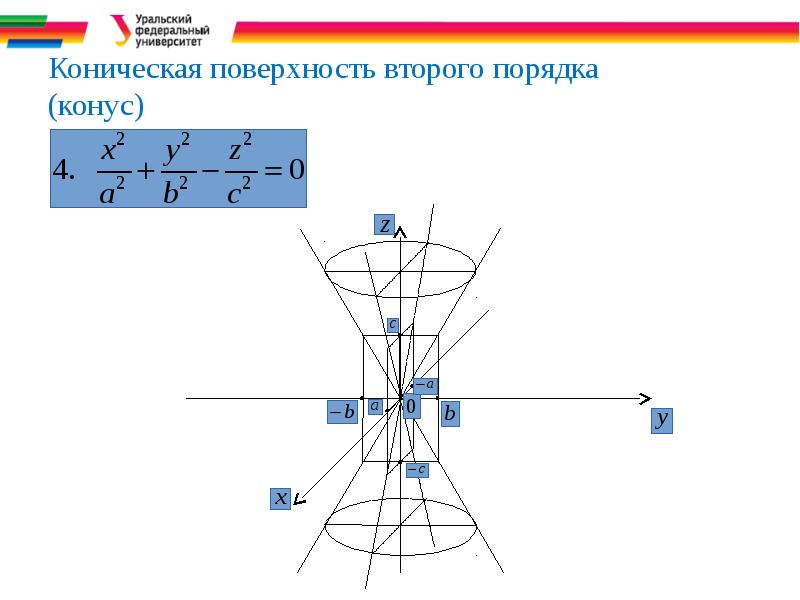
Коническая поверхность второго порядка (конус)

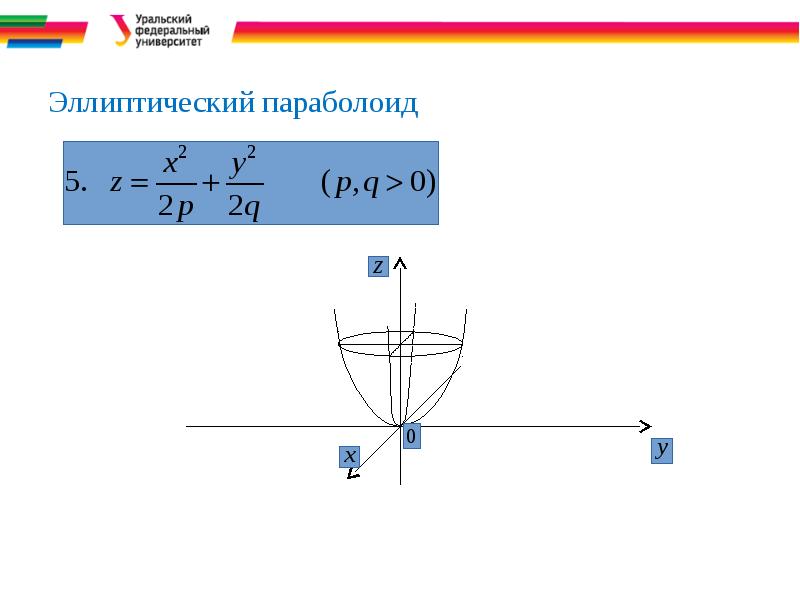
Эллиптический параболоид

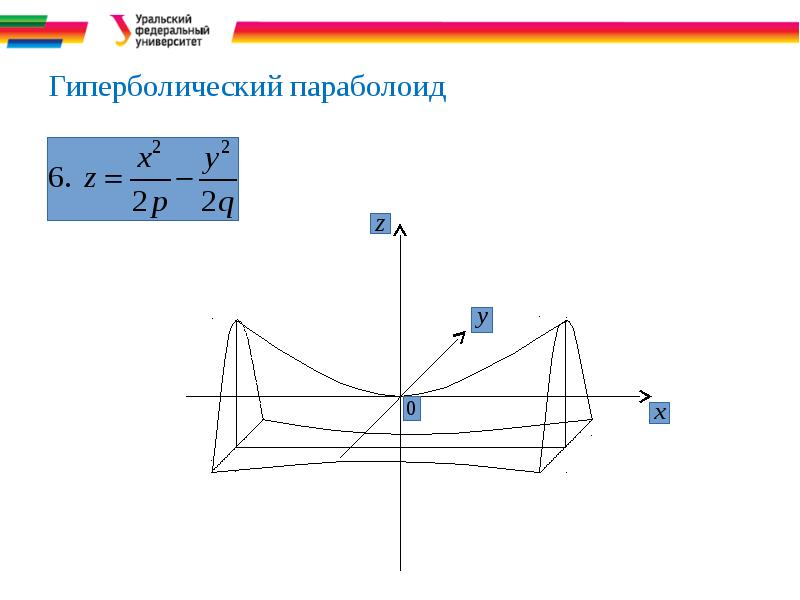
Гиперболический параболоид

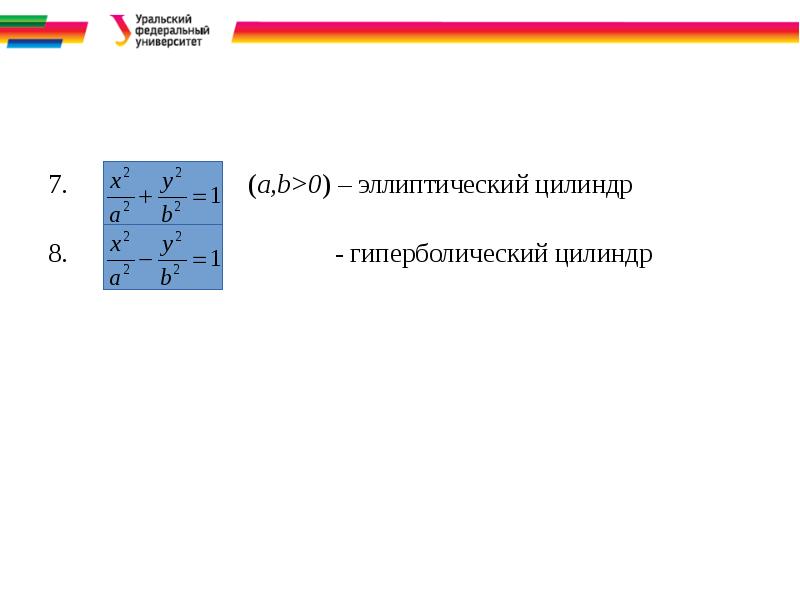
7. (a,b>0) – эллиптический цилиндр 8. - гиперболический цилиндр

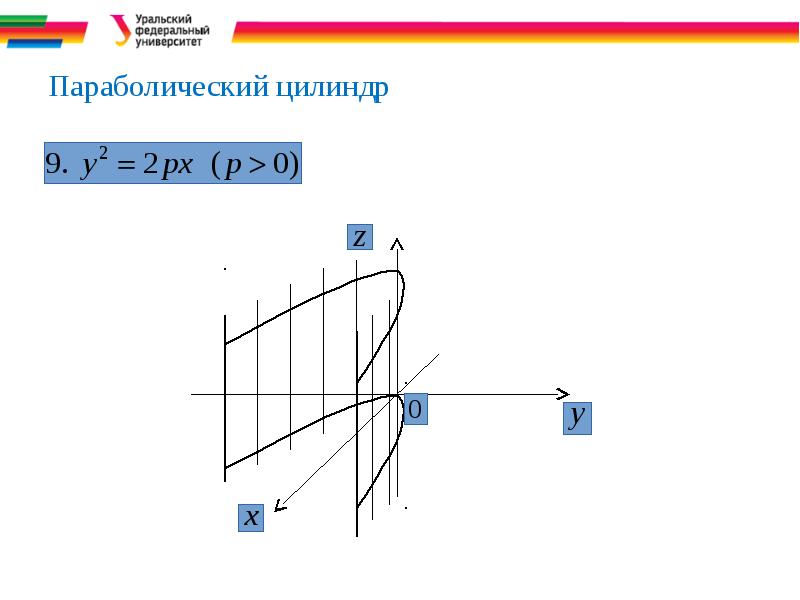
Параболический цилиндр

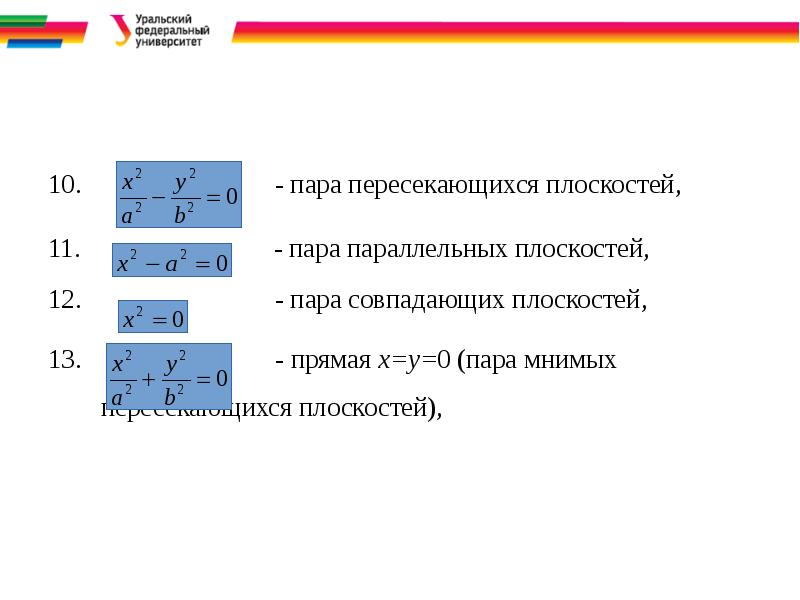
10. - пара пересекающихся плоскостей, 11. - пара параллельных плоскостей, 12. - пара совпадающих плоскостей, - прямая х=у=0 (пара мнимых пересекающихся плоскостей),

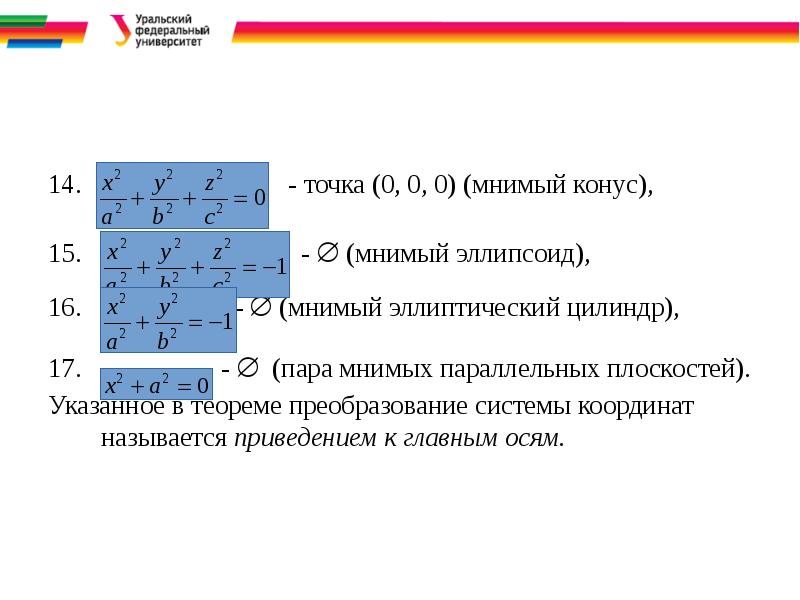
- точка (0, 0, 0) (мнимый конус), -  (мнимый эллипсоид), 16. -  (мнимый эллиптический цилиндр), 17. -  (пара мнимых параллельных плоскостей). Указанное в теореме преобразование системы координат называется приведением к главным осям.

Метод сечений Пересечение исследуемой поверхности с плоскостью дает плоскую кривую. Ряд таких пересечений (называемых сечениями) позволяет выяснить строение поверхности. 1. Эллипсоид. Каноническое уравнение эллипсоида имеет вид: (a>0,b>0,c>0). Исследуем форму эллипсоида по его уравнению.

Метод сечений Из уравнения видно, что эллипсоид представляет собой ограниченную поверхность, заключенную в параллелепипеде Координатные плоскости являются плоскостями симметрии эллипсоида, оси координат – его осями симметрии (все оси эллипсоида вещественны, т.е. их эллипсоид пересекает), начало координат – центром симметрии эллипсоида.

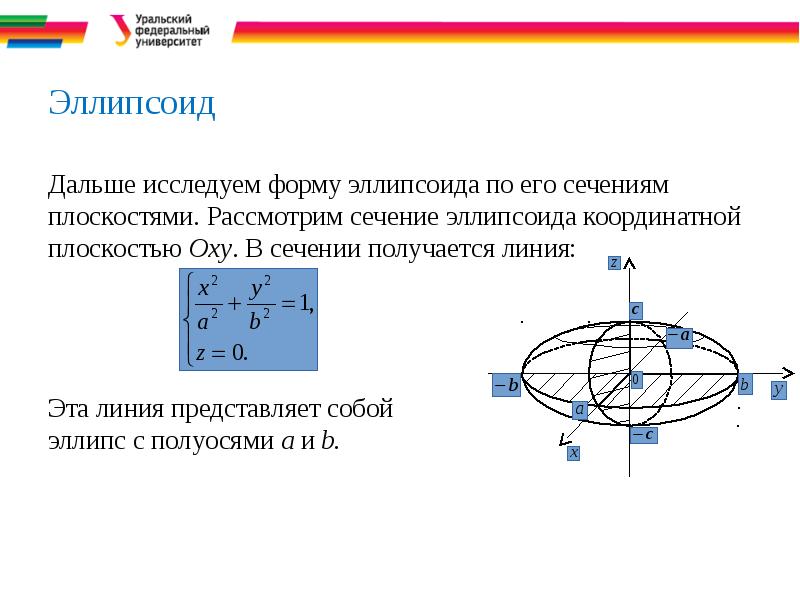
Эллипсоид Дальше исследуем форму эллипсоида по его сечениям плоскостями. Рассмотрим сечение эллипсоида координатной плоскостью Оху. В сечении получается линия: Эта линия представляет собой эллипс с полуосями a и b.

Эллипсоид Аналогично устанавливается сечение данного эллипсоида с плоскостью Oxz - эллипс с полуосями a и с, и с плоскостью Оуz - эллипс с полуосями b и с.

Эллипсоид Рассмотрим теперь сечение эллипсоида с плоскостями , параллельными плоскости Оху. Уравнения линий пересечения будут или

Эллипсоид Если положить , то уравнения запишутся в виде Отсюда видно, что полуоси и являются действительными числами лишь при и линия пересечения эллипсоида с плоскостью z=h представляет собой эллипс с полуосями и .

Эллипсоид При эллипсоид и плоскость пересекаются в одной точке (вырожденный эллипс). Если |h|>c, то эллипсоид и плоскость не имеют общих точек (пересекаются по мнимому эллипсу). Аналогично находим, что в пересечении эллипсоида с плоскостями, параллельными координатным плоскостям Oxz и Oyz, получаются также эллипсы.

Эллипсоид Таким образом, эллипсоид представляет собой ограниченную поверхность, линиями пересечения которой с координатными плоскостями и им параллельными являются эллипсы. Числа a,b,c называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехосным. Если a=b=c, то эллипсоид превращается в сферу. Замечание. Эллипсоид может быть получен равномерным сжатием сферы относительно двух перпендикулярных его плоскостей симметрии.

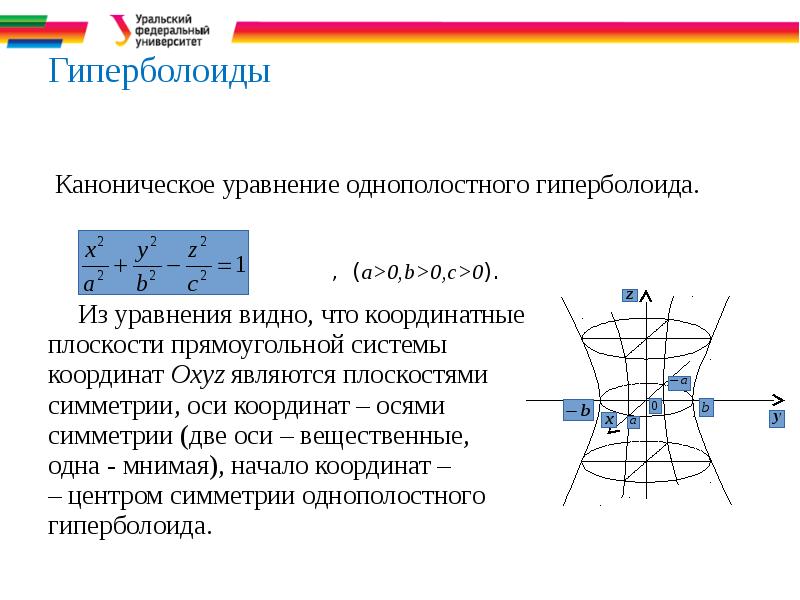
Гиперболоиды Каноническое уравнение однополостного гиперболоида. , (a>0,b>0,c>0). Из уравнения видно, что координатные плоскости прямоугольной системы координат Охуz являются плоскостями симметрии, оси координат – осями симметрии (две оси – вещественные, одна - мнимая), начало координат – – центром симметрии однополостного гиперболоида.

Гиперболоид Исследуем форму этого гиперболоида по его сечениям координатными и параллельными им плоскостями. Линия пересечения гиперболоида с плоскостью Оху имеет уравнения:

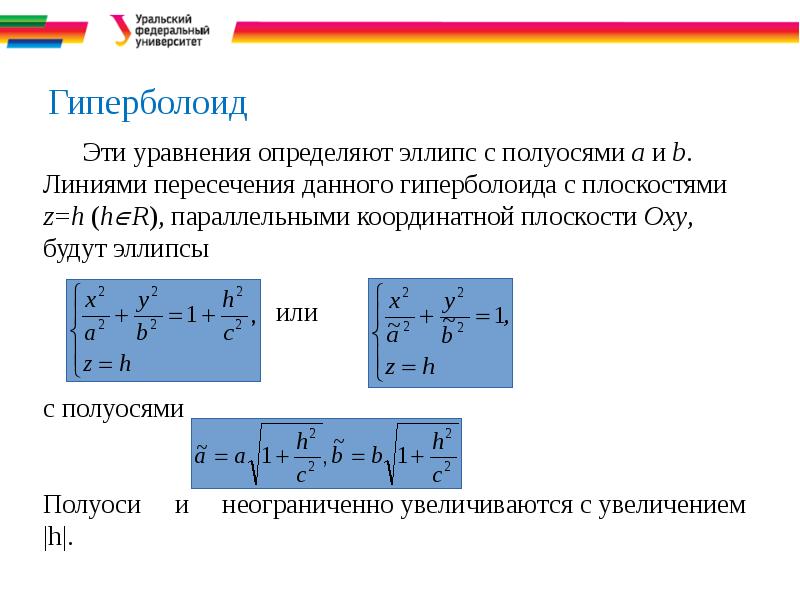
Гиперболоид Эти уравнения определяют эллипс с полуосями а и b. Линиями пересечения данного гиперболоида с плоскостями z=h (hR), параллельными координатной плоскости Оху, будут эллипсы или с полуосями Полуоси и неограниченно увеличиваются с увеличением |h|.

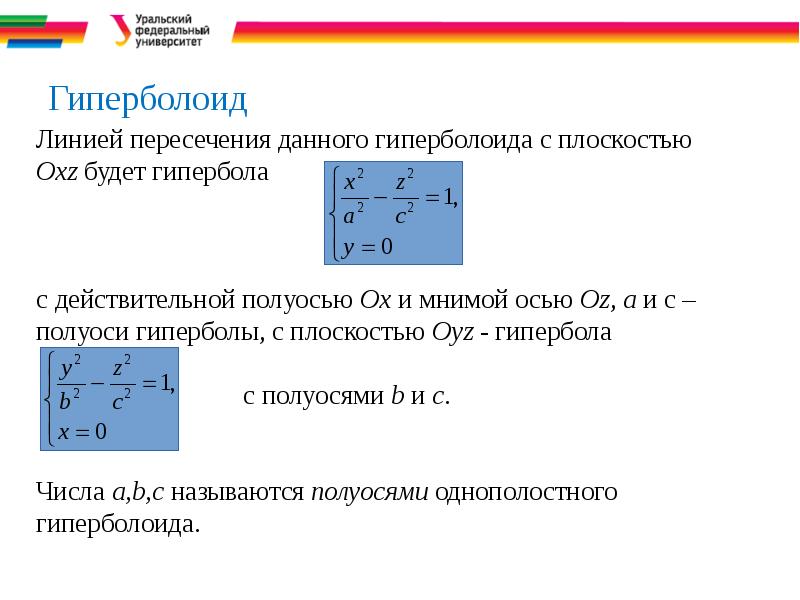
Гиперболоид Линией пересечения данного гиперболоида с плоскостью Oxz будет гипербола с действительной полуосью Ox и мнимой осью Oz, а и с – полуоси гиперболы, с плоскостью Оуz - гипербола с полуосями b и с. Числа a,b,c называются полуосями однополостного гиперболоида.

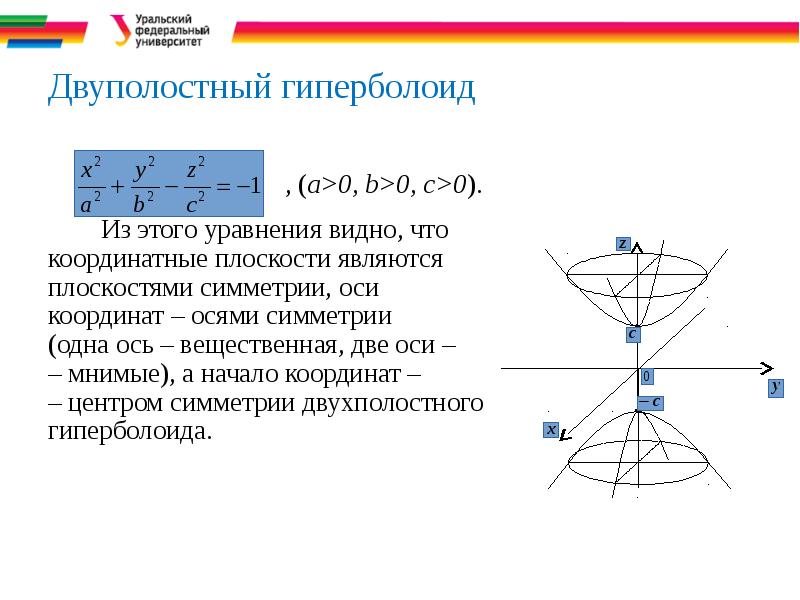
Двуполостный гиперболоид , (a>0, b>0, c>0). Из этого уравнения видно, что координатные плоскости являются плоскостями симметрии, оси координат – осями симметрии (одна ось – вещественная, две оси – – мнимые), а начало координат – – центром симметрии двухполостного гиперболоида.

Двуполостный гиперболоид В сечении данного гиперболоида с координатной плоскостью Оху получается мнимый эллипс: Это значит, что плоскость z=0 не пересекает гиперболоид.

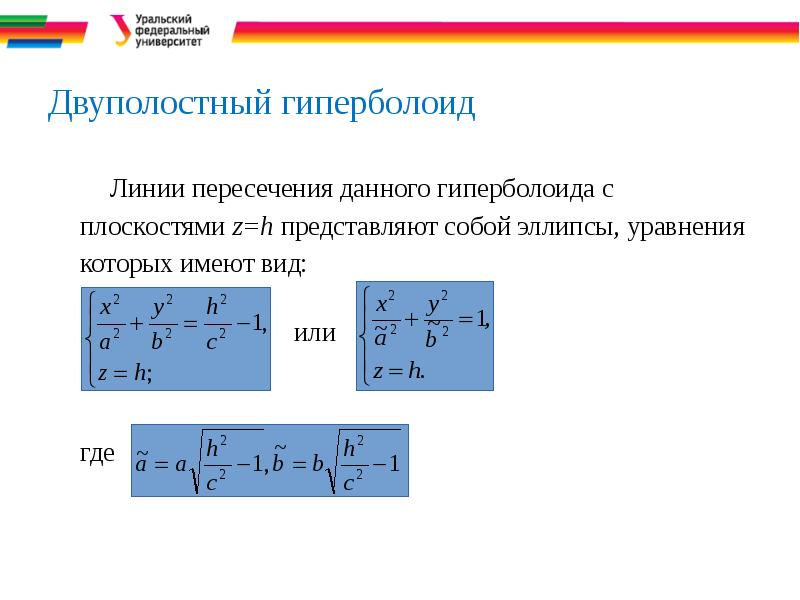
Двуполостный гиперболоид Линии пересечения данного гиперболоида с плоскостями z=h представляют собой эллипсы, уравнения которых имеют вид: или где

Двуполостный гиперболоид Полуоси и являются действительными числами лишь при Это означает, что в пространстве между плоскостями z=с и z= – с не содержится точек рассматриваемой поверхности. Эта поверхность состоит из двух полостей, расположенных так, как показано на рисунке.

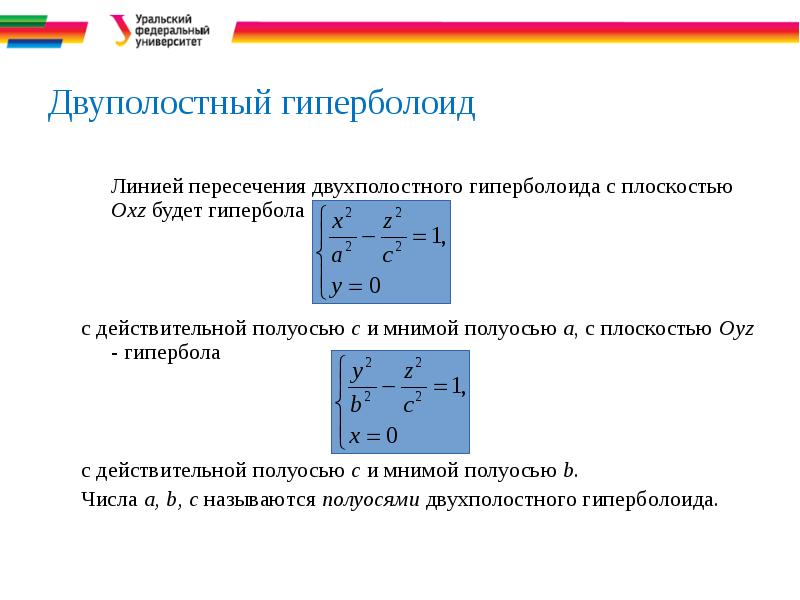
Двуполостный гиперболоид Линией пересечения двухполостного гиперболоида с плоскостью Oxz будет гипербола с действительной полуосью с и мнимой полуосью а, с плоскостью Оуz - гипербола с действительной полуосью с и мнимой полуосью b. Числа a, b, c называются полуосями двухполостного гиперболоида.

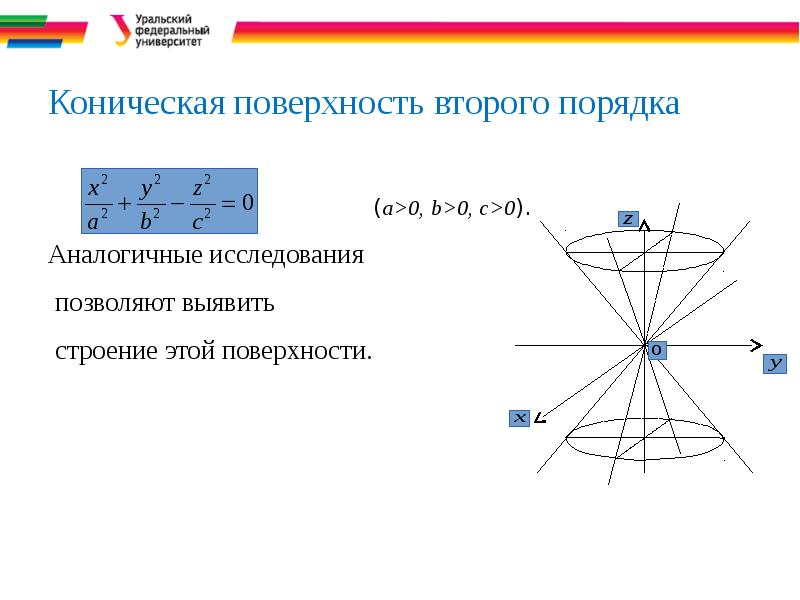
Коническая поверхность второго порядка (a>0, b>0, c>0). Аналогичные исследования позволяют выявить строение этой поверхности.

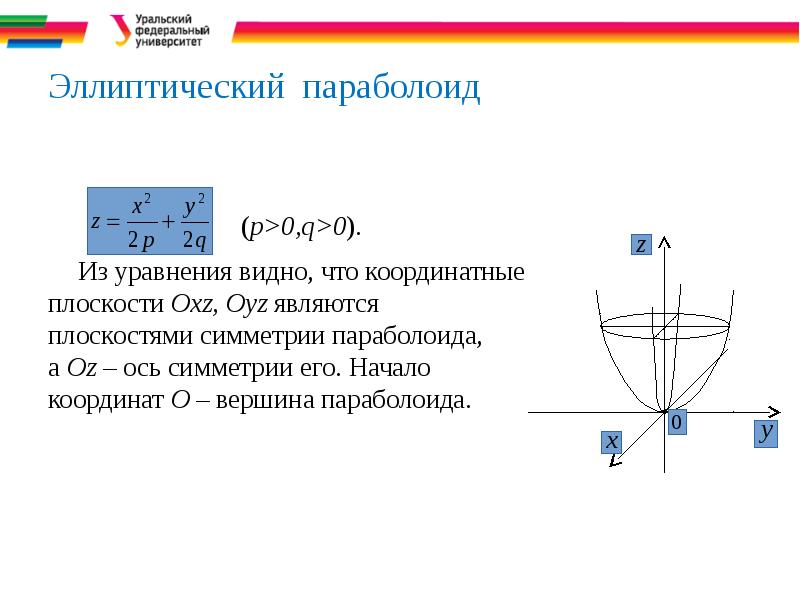
Эллиптический параболоид (p>0,q>0). Из уравнения видно, что координатные плоскости Охz, Оуz являются плоскостями симметрии параболоида, а Oz – ось симметрии его. Начало координат О – вершина параболоида.