Зеркальная симметрия в геометрии

Зеркальная симметрия

Симметрия - это гармония в расположении одинаковых предметов какой-либо группы или частей в одном предмете, причем расположение определяется одной или несколькими воображаемыми зеркальными плоскостями.

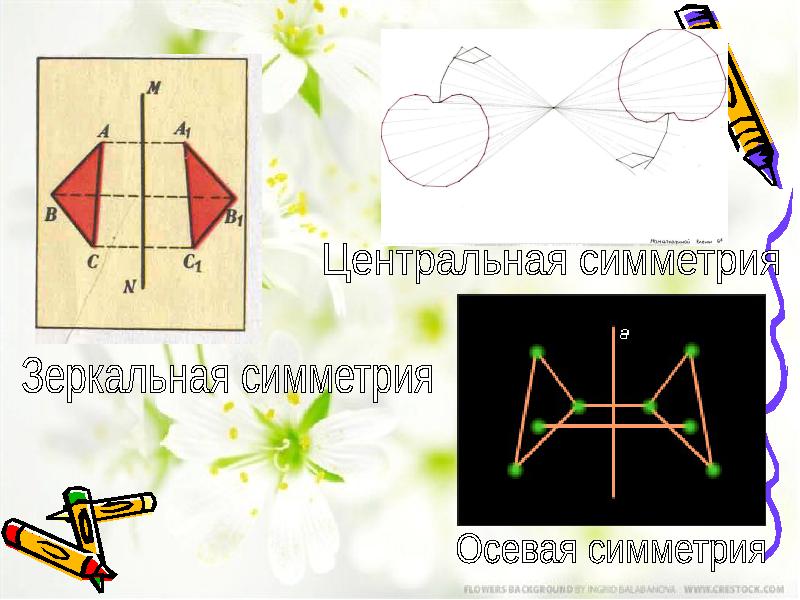
Виды симметрии а) Лучевая симметрия  б) Осевая симметрия в) Центральная симметрия г) Зеркальная симметрия

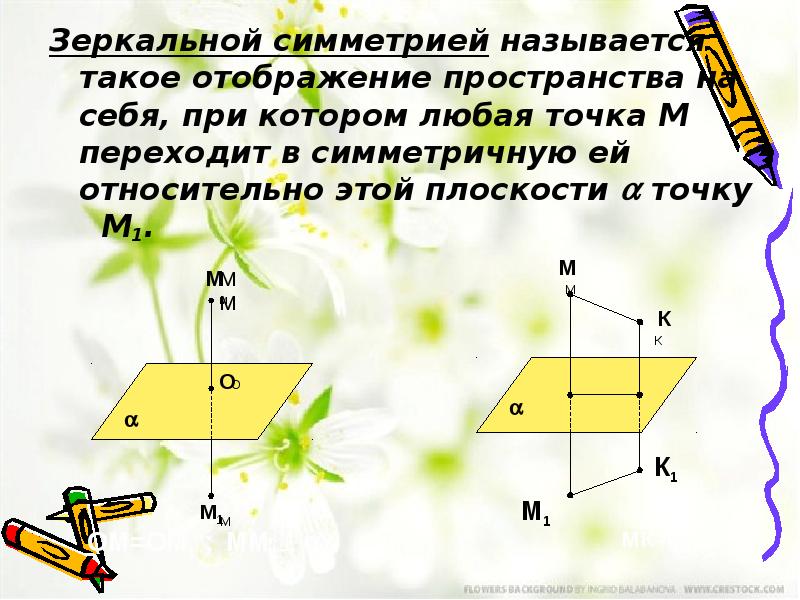
Зеркальной симметрией называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно этой плоскости  точку М1.

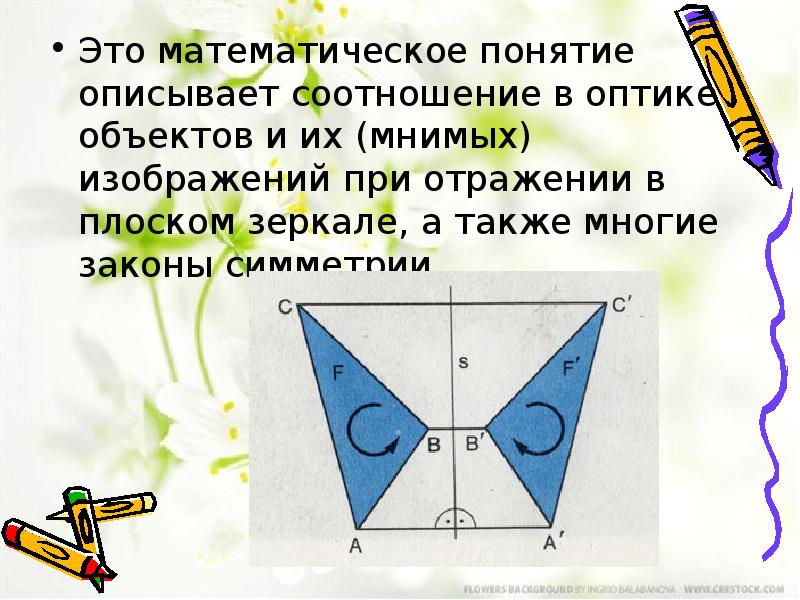
Это математическое понятие описывает соотношение в оптике объектов и их (мнимых) изображений при отражении в плоском зеркале, а также многие законы симметрии.

Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для каждой точки E этой фигуры может быть найдена точка E1 этой же фигуры, так что отрезок EE1 перпендикулярен плоскости S и делится этой плоскостью пополам ( EA = AE1 ). Плоскость S называется плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова. Они называются зеркально равными.

Зеркало не просто копирует объект, а меняет местами (переставляет) передние и задние по отношению к зеркалу части объекта. Зеркальный двойник оказывается "вывернутым" вдоль направления перпендикулярного к плоскости зеркала.

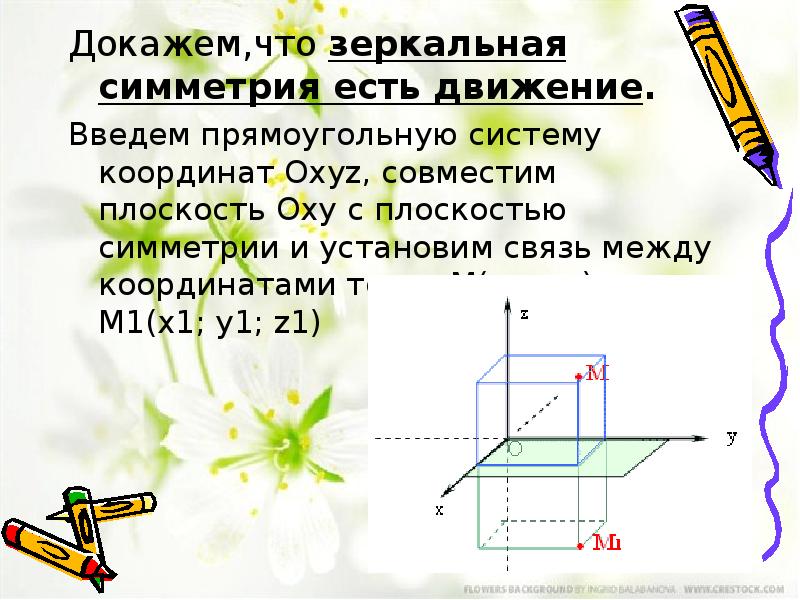
Докажем,что зеркальная симметрия есть движение. Введем прямоугольную систему координат Оxyz, совместим плоскость Оxy с плоскостью симметрии и установим связь между координатами точек M(x; y; z) и M1(x1; y1; z1)

Если М не лежит в плоскости Оху, то х =х1, у =у1, z = -z1. Если М I Оху , то x=x1, y=y1, z=z1=0 Рассмотрим А(x1; y1; z1), В(x2; y2; z2), А—> А1, В—> В1 , тогда А1(x1; y1; -z1), В1(x2; y2; -z2), тогда АВ=А1В1, т.е.Оху – движение.

Зеркально осевая симметрия.  Если плоская фигура ABCDE  ( рис.107 ) симметрична относительно плоскости S  ( что возможно, если только  плоская фигура перпендикулярна плоскости S ), то прямая KL,  по которой эти плоскости пересекаются, являетсяосью  симметрии  фигуры ABCDE. В этом случае фигура ABCDE называетсязеркально-симметричной.

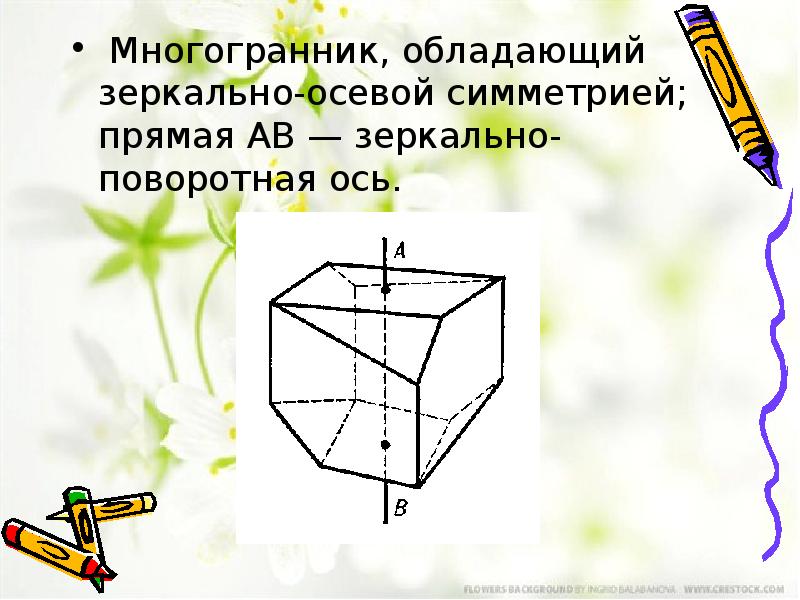
 Многогранник, обладающий зеркально-осевой симметрией; прямая AB — зеркально-поворотная ось.

Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.

Каждая деталь в симметричной системе существует как двойник своей обязательной паре, расположенной по другую сторону оси, и благодаря двойственности отдельных элементов сооружение “читается” целиком даже при восприятии с одной стороны. Каждая деталь в симметричной системе существует как двойник своей обязательной паре, расположенной по другую сторону оси, и благодаря двойственности отдельных элементов сооружение “читается” целиком даже при восприятии с одной стороны.

Зеркальная симметрия-это симметрия окружающего нас мира. Построение изображения с помощью зеркальной симметрии сходно с изображением в зеркале.

Зеркальная симметрия в природе