Лабораторная работа №3. Статистический анализ точности обработки деталей на бесцентрово-шлифовальном станке презентация
Содержание
- 2. Партия – детали, запускаемые в обработку одновременно и обрабатываемые на одном
- 3. Классификация и законы распределения погрешностей. Классификация и законы распределения погрешностей. Систематически-постоянными
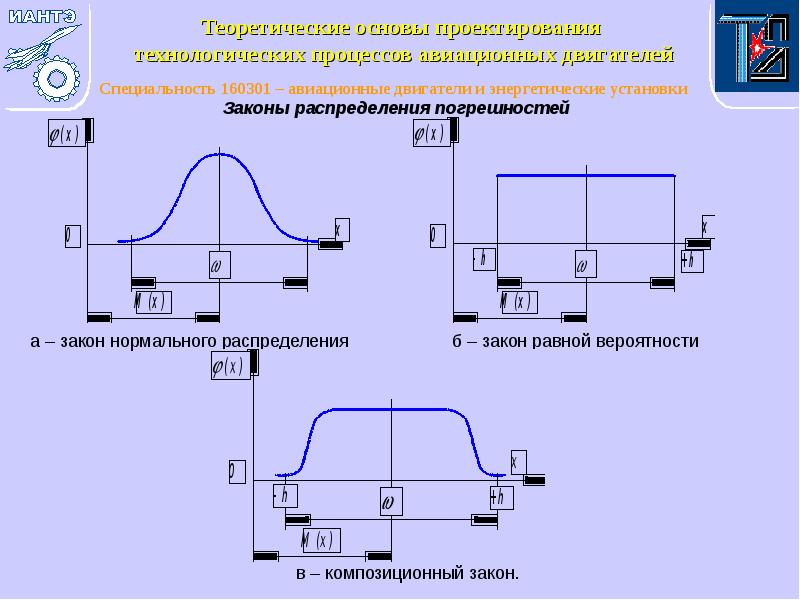
- 4. Законы распределения погрешностей Законы распределения погрешностей а –
- 5. Основные характеристики закона Гаусса Основные характеристики закона Гаусса математическое
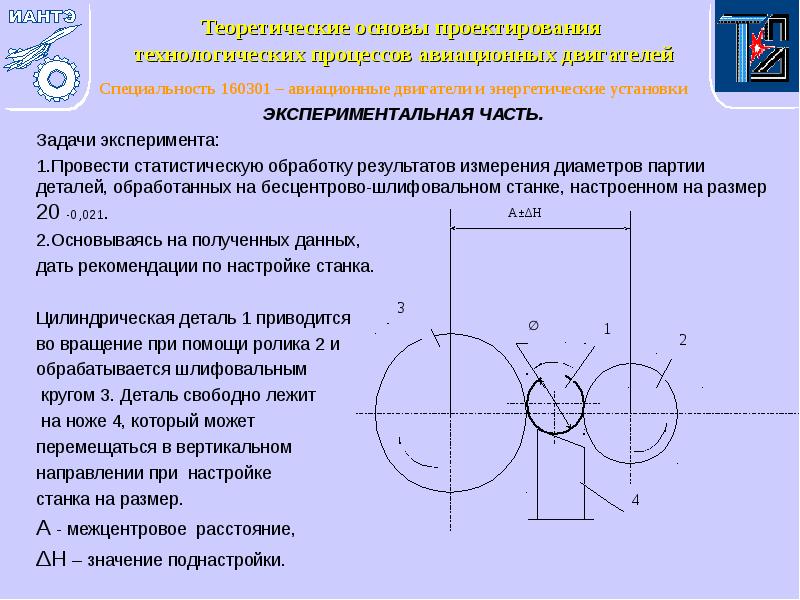
- 6. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ. Задачи эксперимента: 1.Провести статистическую обработку результатов измерения
- 7. Порядок выполнения работы Порядок выполнения работы Измерить с помощью оптиметра отклонения
- 8. 4.У каждой детали измеряем отклонение ΔΧ и заносим в протокол измерений
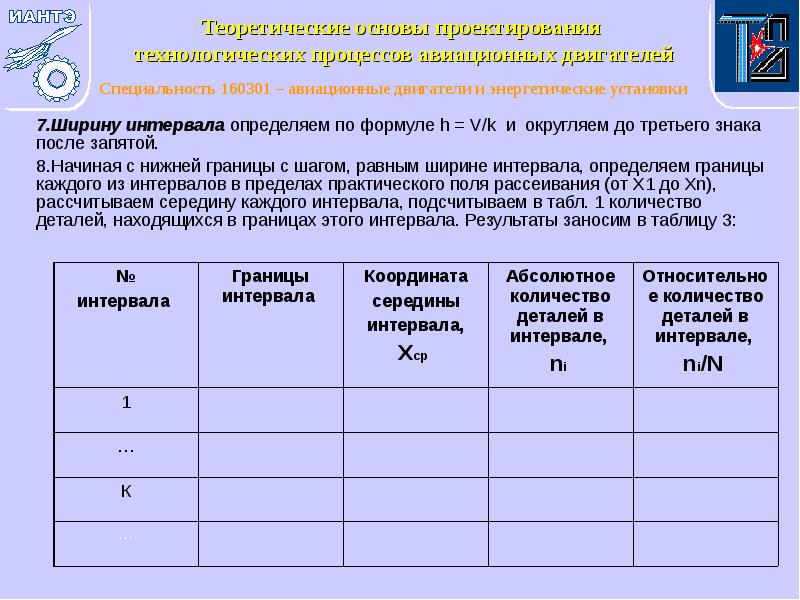
- 9. 7.Ширину интервала определяем по формуле h = V/k и округляем до
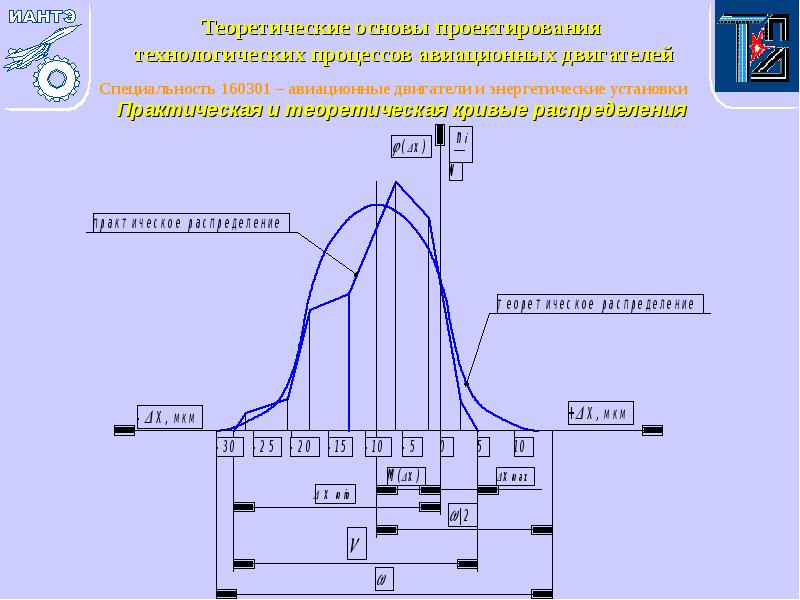
- 10. 9.Строим практическую кривую распределения. По оси абсцисс откладываем координаты середин интервалов
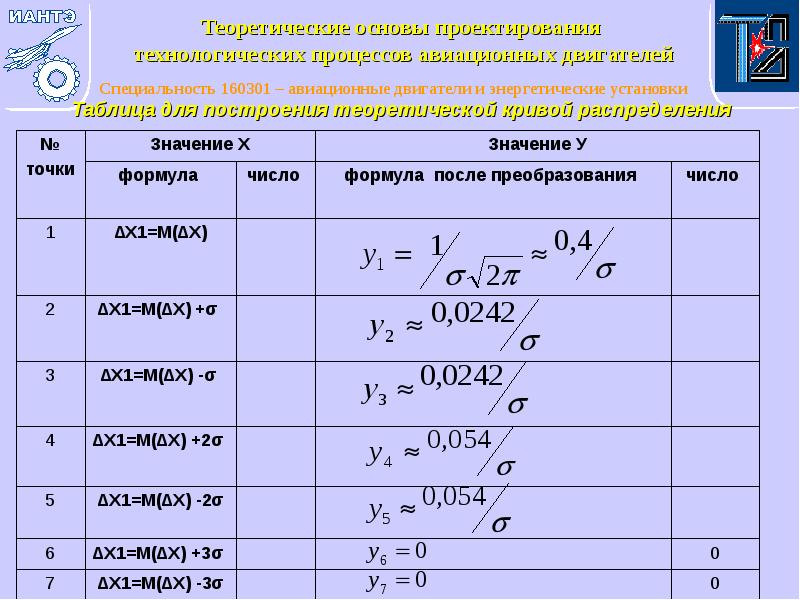
- 11. Таблица для построения теоретической кривой распределения
- 12. Практическая и теоретическая кривые распределения
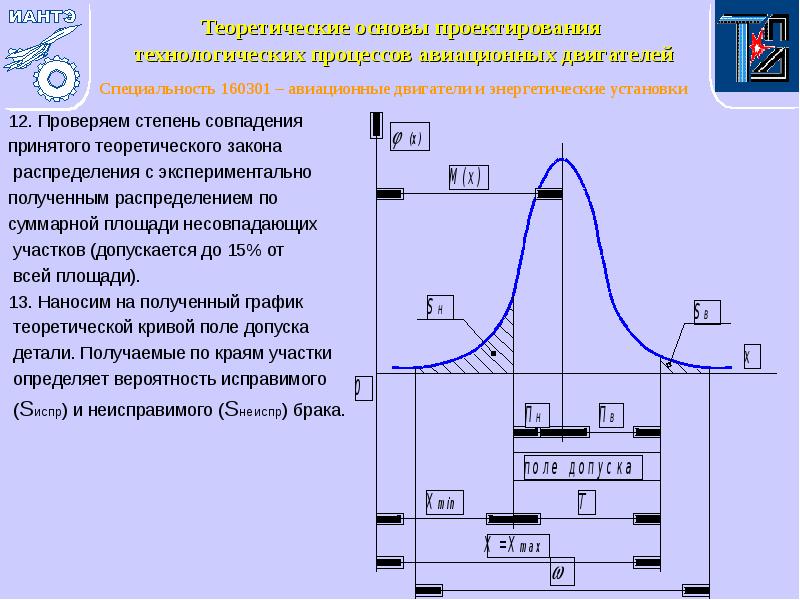
- 13. 12. Проверяем степень совпадения 12. Проверяем степень совпадения принятого теоретического закона
- 14. 14. Выводы по работе должны содержать заключение: 14. Выводы по работе
- 15. Скачать презентацию








Слайды и текст этой презентации
Скачать презентацию на тему Лабораторная работа №3. Статистический анализ точности обработки деталей на бесцентрово-шлифовальном станке можно ниже:
Похожие презентации





























