Длина окружности
Содержание
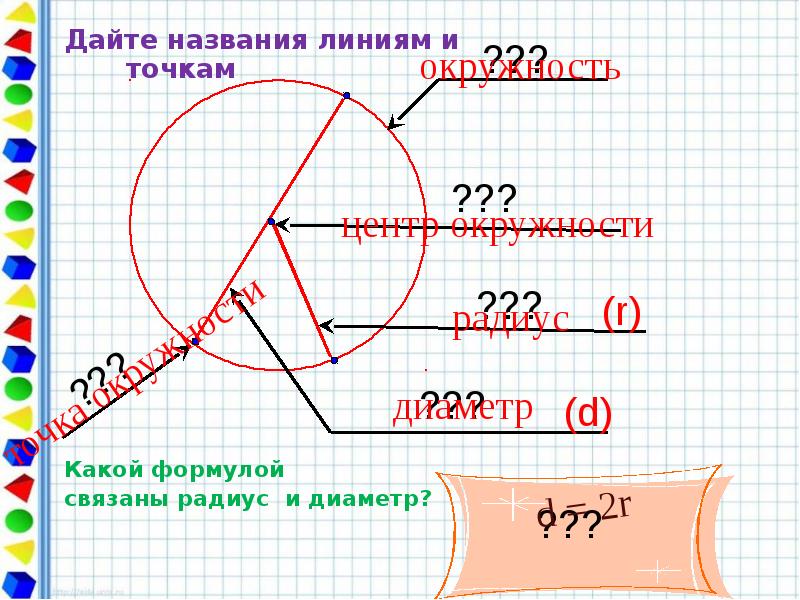
- 2. Дайте названия линиям и точкам Дайте названия линиям и точкам
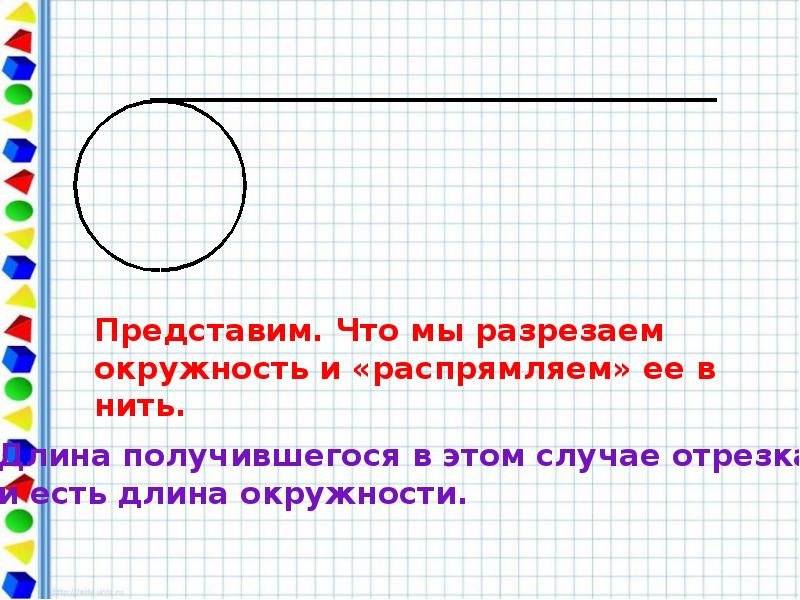
- 3. Длину отрезка можно измерить с помощью линейки, длину ломаной можно найти,
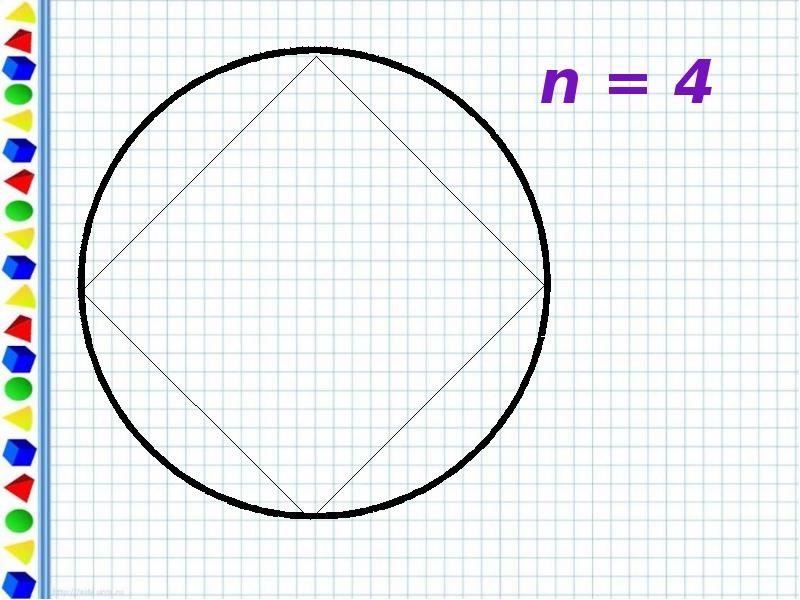
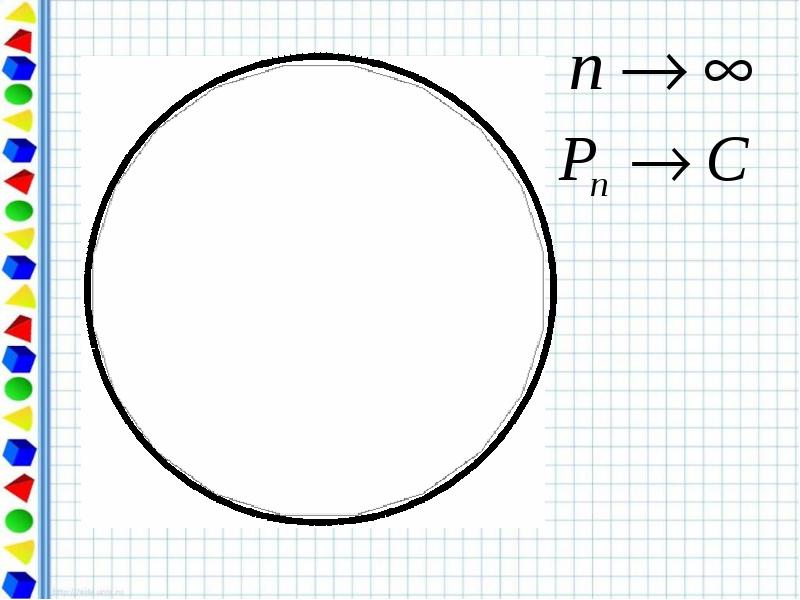
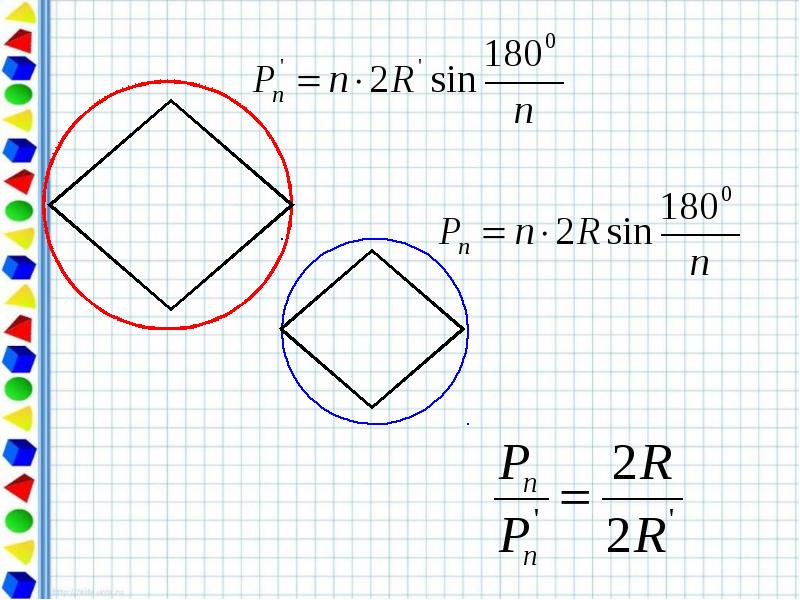
- 10. Периметр любого вписанного в окружность многоугольника является приближённым значением длины
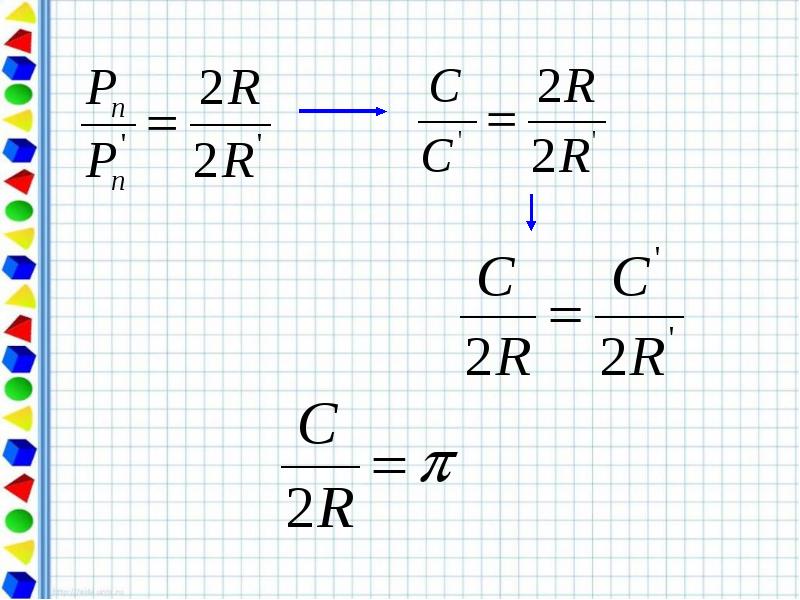
- 14. Свойство длины окружности. Отношение длины окружности к её диаметру есть одно
- 19. Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне
- 20. Вычислением числа занимались в более поздние века многие знаменитые математики.
- 24. Теперь известно, что число иррациональное, может быть представлено в виде
- 27. Задачи по теме «Длина окружности»
- 28. Теоретические сведения
- 29. Задача: 1) вычислить длину окружности, если ее диаметр равен 6 см
- 30. Решение: 1) D=6 см С= 3,14• 6 =18,84 (см)
- 31. Задача: Длина окружности цирковой арены равна 41 м. Найдите диаметр
- 32. Решение:
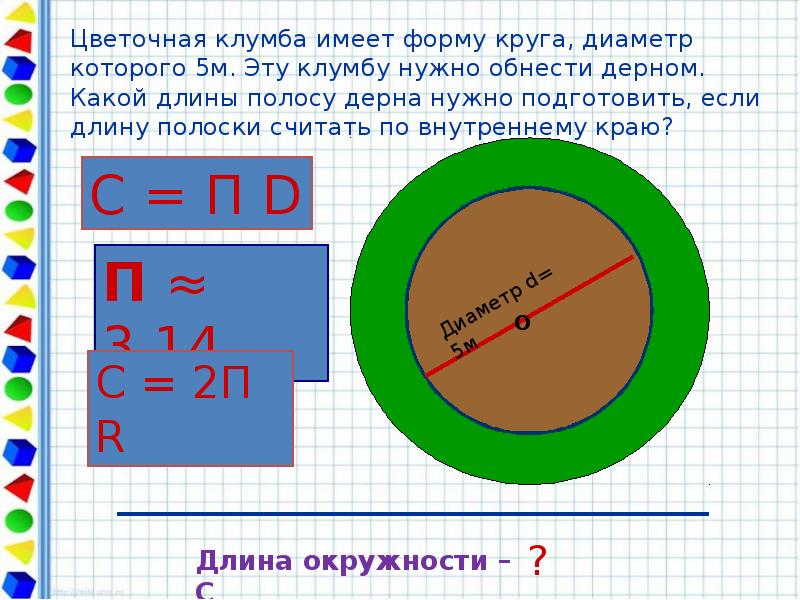
- 34. С = 3,14•5=15,7 (м) Ответ: длина полосы дерна равна 15,7 м
- 36. Решите задачу
- 37. Решение
- 38. Отлитый в 1735 г. Царь колокол, хранящийся в Московском Кремле, имеет
- 39. Решите задачу
- 40. Решите задачу
- 41. Решите задачу
- 42. Задача (О Тунгусском метеорите, 1908 г.)
- 43. Древнегреческий математик Архимед установил, что длина окружности относится к длине диаметра
- 44. Вообразите, что вы обошли землю по экватору. На сколько при этом
- 45. Если обтянуть земной шар по экватору проволокой и затем прибавить к
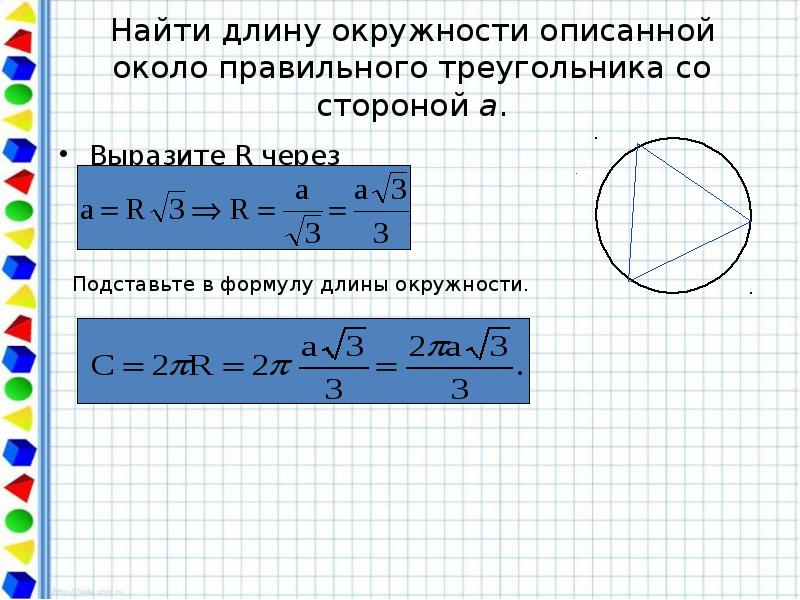
- 46. Найти длину окружности описанной около правильного треугольника со стороной а. Выразите
- 47. Найти длину окружности описанной около равнобедренного треугольника с основанием а и
- 48. Найти длину окружности описанной около равнобедренного треугольника с основанием a и
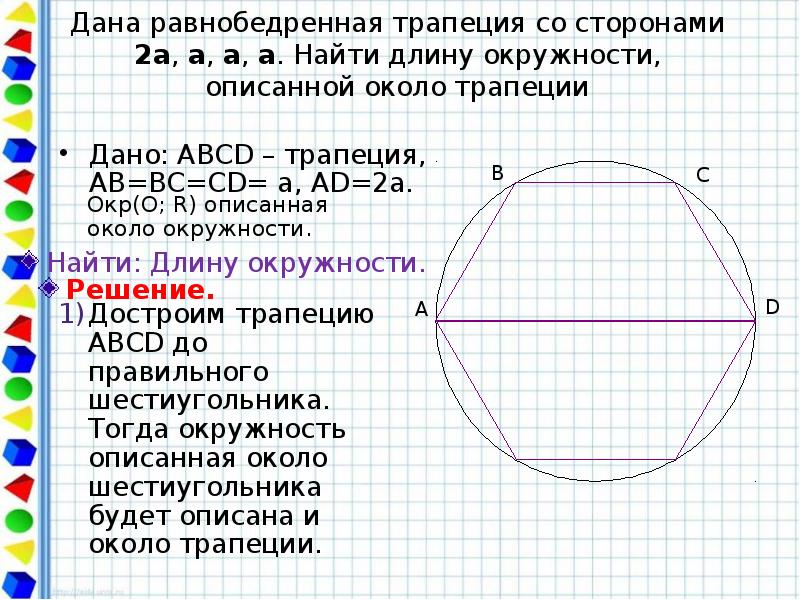
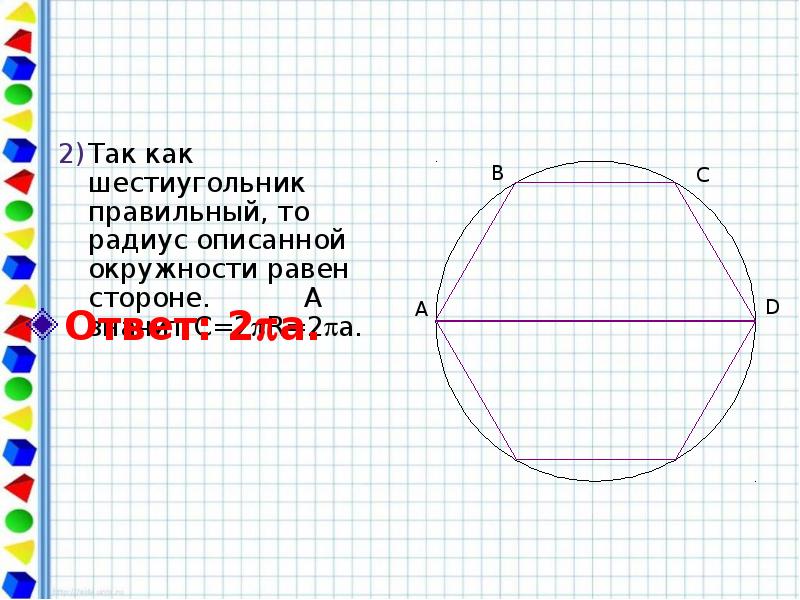
- 49. Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину
- 53. Интересные факты Отношение длины основания Великой Пирамиды к ее высоте,
- 54. Интересные факты Лидером по тупым законам по праву может считаться
- 56. Скачать презентацию






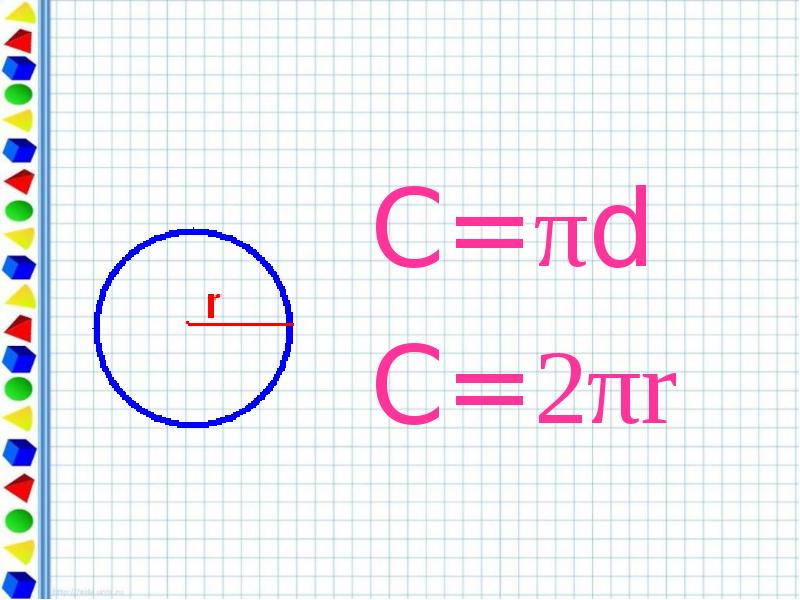






































Слайды и текст этой презентации
Похожие презентации