Осевая и центральная симметрии

Осевая и центральная симметрии. Данная презентация изготовлена учителем математики Сосенской средней щколы N1 Градовой Л. М.

Содержание. 1. Осевая симметрия. 2. Фигуры, содержащие ось симметрии. 3. Фигуры, имеющие две оси симметрии. 4. Фигуры, имеющие более двух осей симметрии. 5. Фигуры, не имеющие осей симметрии 6. Центральная симметрия. 7. Фигура симметричная, относительно точки. 8. Фигуры, обладающие центральной симметрией. 9. Симметрия предметов на плоскости. 10. Конец.

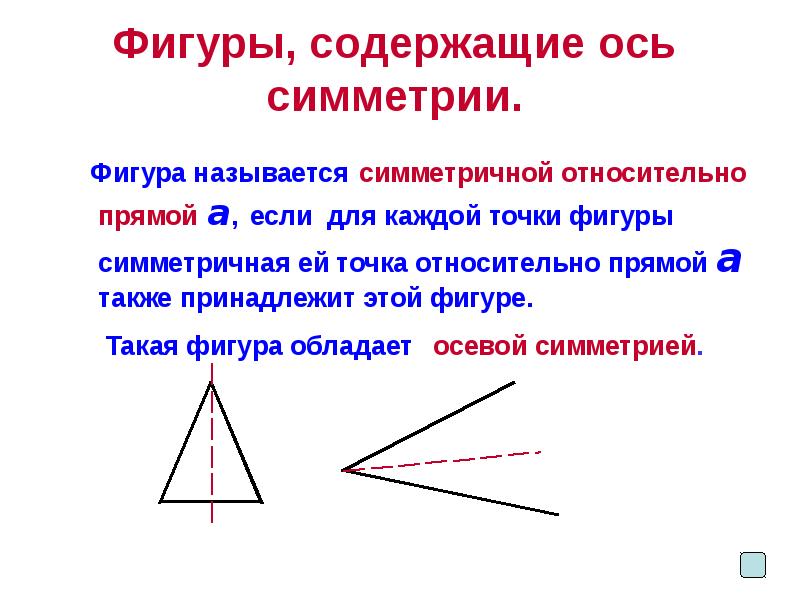
Осевая симметрия. Две точки А и А1 называются симметричными относительно прямой a, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. А а А1

Фигуры, содержащие ось симметрии. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Такая фигура обладает осевой симметрией.

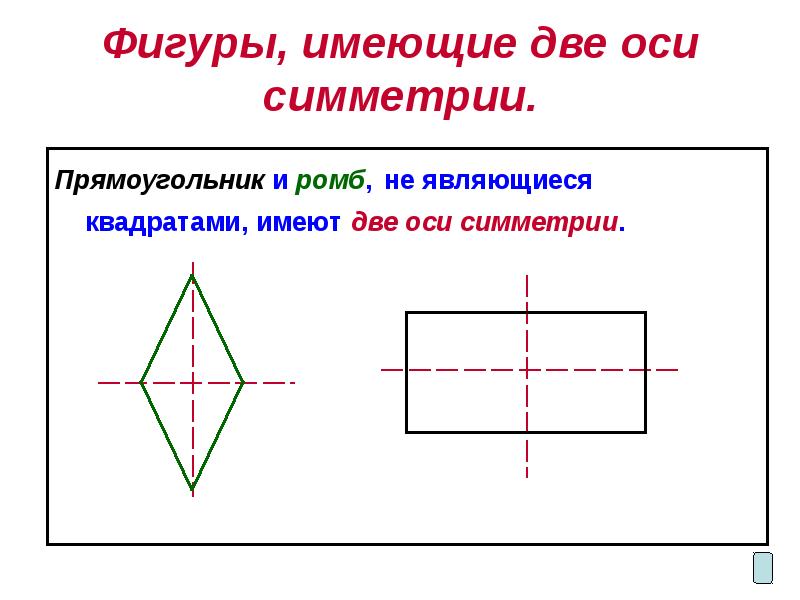
Фигуры, имеющие две оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют две оси симметрии.

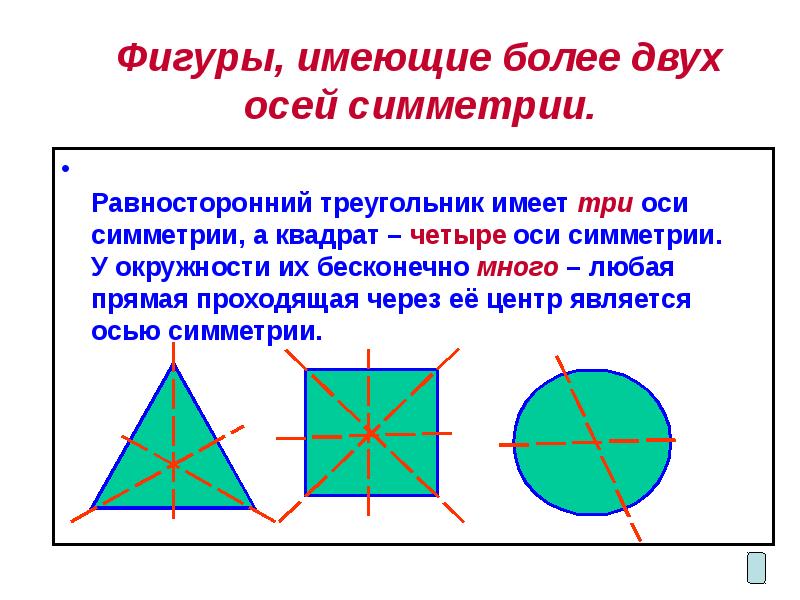
Фигуры, имеющие более двух осей симметрии. Равносторонний треугольник имеет три оси симметрии, а квадрат – четыре оси симметрии. У окружности их бесконечно много – любая прямая проходящая через её центр является осью симметрии.

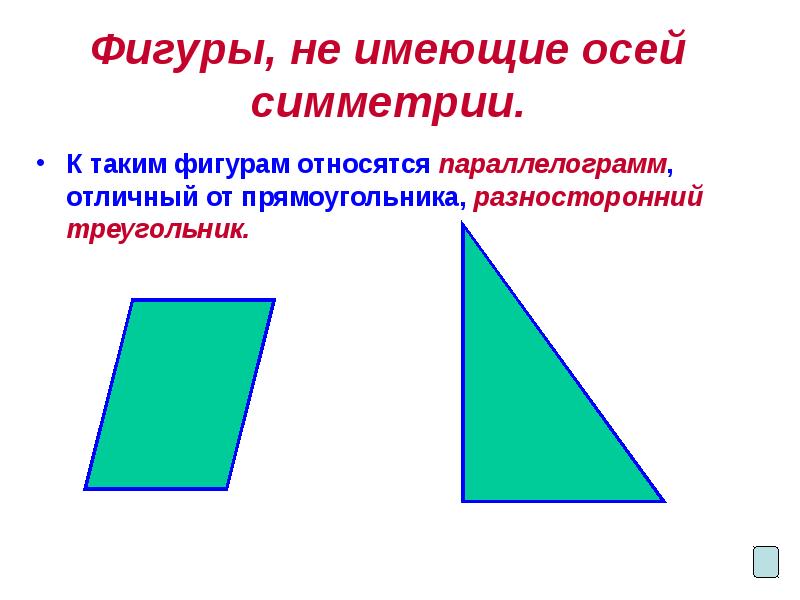
Фигуры, не имеющие осей симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

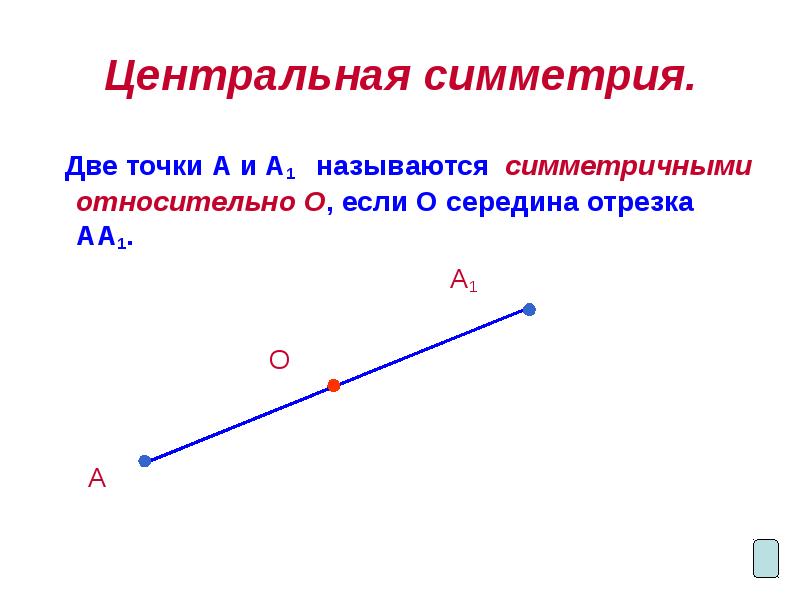
Центральная симметрия. Две точки А и А1 называются симметричными относительно О, если О середина отрезка АА1. А1 О А

Фигура, симметричная, относительно точки. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии. Такая фигура обладает центральной симметрией. В А О Любая точка прямой является центром симметрии.

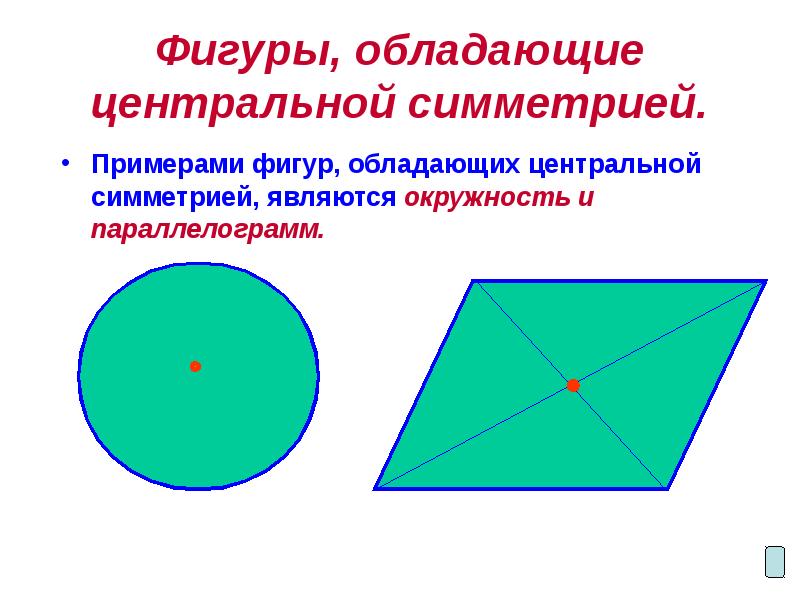
Фигуры, обладающие центральной симметрией. Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм.

Симметрия предметов на плоскости. Изображения предметов на плоскости из окружающего мира имеет ось или центр симметрии. С симметрией мы встречаемся в природе, быту, архитектуре и технике.

Симметрия в быту.

Симметрия в науке и технике.

Симметрия в архитектуре.

Конец