Теория стереопары снимков презентация
Содержание
- 2. 5.1 Элементы ориентирования стереопары По одиночному снимку можно получить лишь две
- 3. На практике фотографирование с двух точек базиса чаще всего выполняют одной
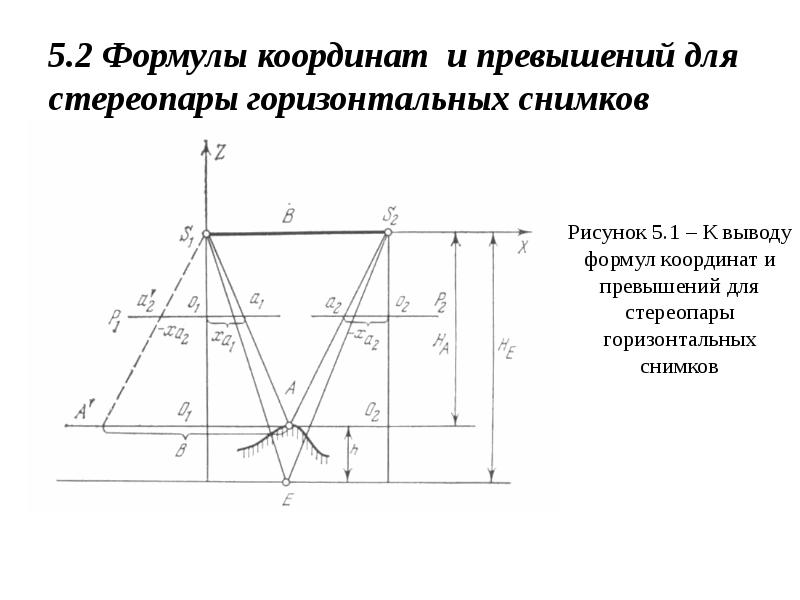
- 7. 5.2 Формулы координат и превышений для стереопары горизонтальных снимков
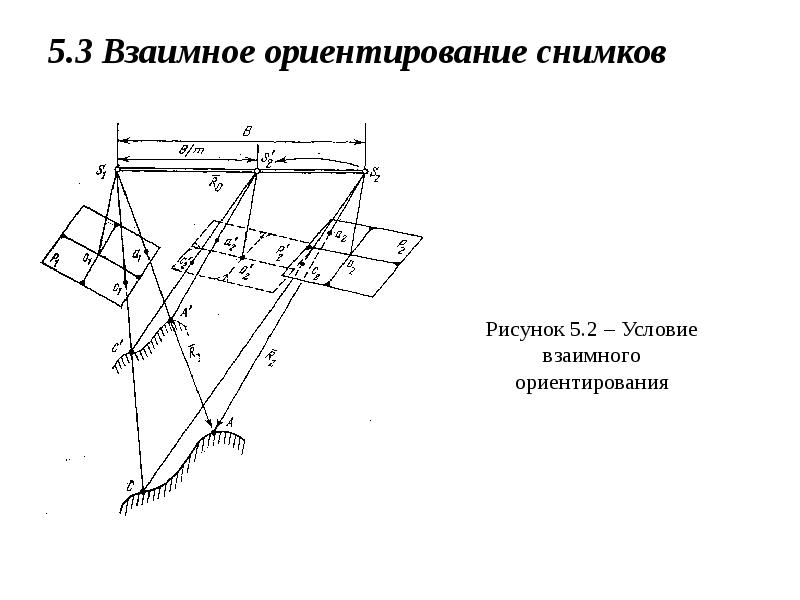
- 14. Взаимное ориентирование двух снимков стереопары можно выполнить двумя основными способами:
- 24. Если элементы внешнего ориентирования модели известны, то геодезические координаты Хг, Уг,
- 25. В формулах 5.12 семь неизвестных элементов внешнего ориентирования. Одна опорная геодезическая
- 27. Скачать презентацию
























Слайды и текст этой презентации
Похожие презентации