Исследование математических моделей

Исследование математических моделей

Пусть задана функция f(x). Требуется найти корни уравнения f (x)=0 (1) Задача нахождения корней уравнения (1) обычно решается в два этапа. На первом этапе изучается расположение корней и проводится их разделение, то есть выделяются области, содержащие только один корень. На втором этапе, используя начальное приближение, строится итерационный процесс для уточнений корня.

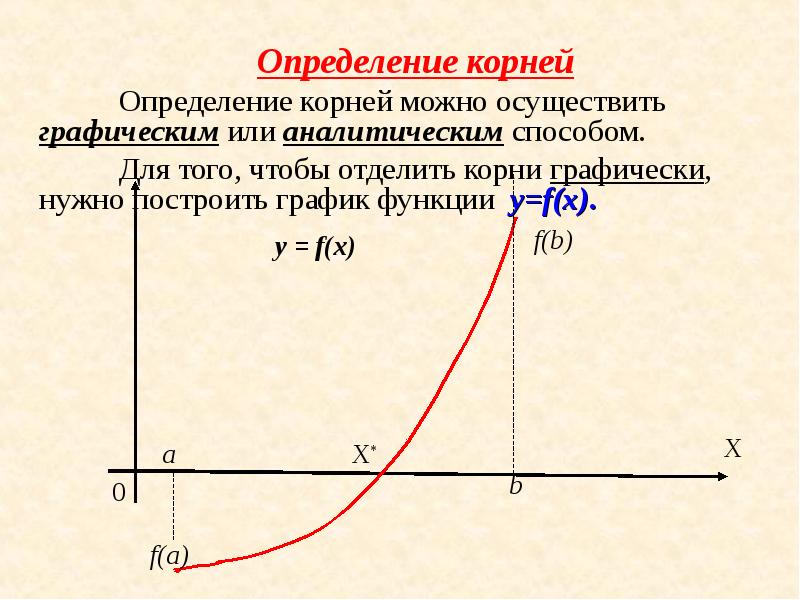
Определение корней Определение корней можно осуществить графическим или аналитическим способом. Для того, чтобы отделить корни графически, нужно построить график функции y=f(x).

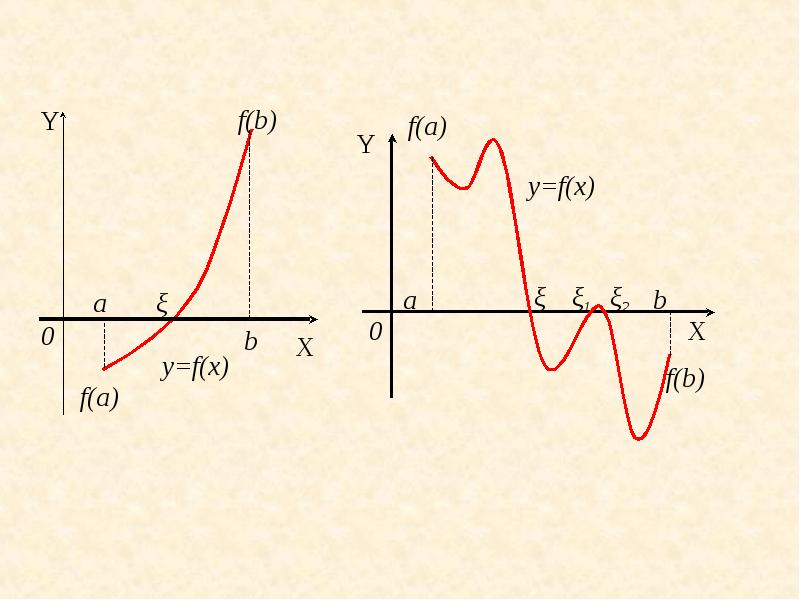
Для определения корней аналитически используем следующее утверждение: если функция f(x) принимает значения разных знаков на концах отрезка [a, b], т.е. f(a) f(b)<0, то внутри этого отрезка содержится, по меньшей мере, один корень уравнения f(x)=0 .

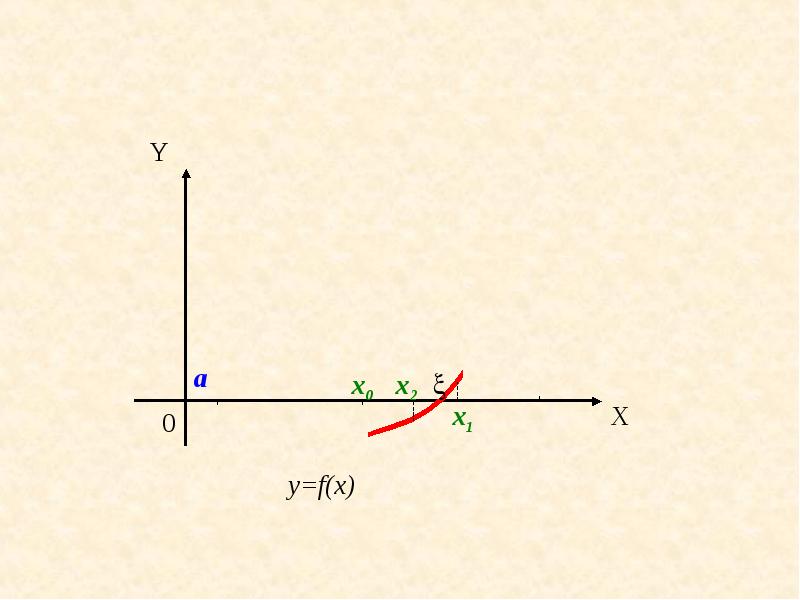
Метод половинного деления Предположим что в интервале [a, b] расположен один корень уравнения (1). Найдем точку c= (b+a) /2. Это x0. Далее, если f( c)* f( a) >0, то b = c, если f( c)* f( b) >0, то a = c. Аналогично находим следующие приближения xn (n=1,2,…) Если выполняется одно из условий : | f(xn+1) |   или | xn-xn+1 |  , где  - заданная точность вычислений, то корень уравнения f(x)=0 найден =x*= xn+1 и процесс вычисления заканчивается.