Логарифмические неравенства
Содержание
- 2. При изучении логарифмических функций рассматриваются неравенства вида: logax < b
- 3. logax > logay x>0; y>0 eсли а>0, то x>y eсли 0<a<1,
- 4. Пример №1 Решить неравенство: log 3(x+2)<3 log 3(x+2)<log333 a=3; 3>0 =>
- 5. Пример №2 Решить неравенство:log0,5(2x+1)>-2 a=0,5; 0<0,5<1 => функция убывает log0,5
- 6. Решите устно: log2x>1 ответы: (2;∞) log3x>2 (9;∞)
- 7. log2x≤1 ответы: (0;2] log3x<2
- 8. Решите неравенства: log3(x-2)>1 a>1 = >функция возрастает x-2>3 x-2>3 x>5 x-2>0
- 9. lg(x-3)≥2 a>1 = >функция возрастает x-3≥100 x-3≥100 x≥103 x-3>0
- 10. Скачать презентацию


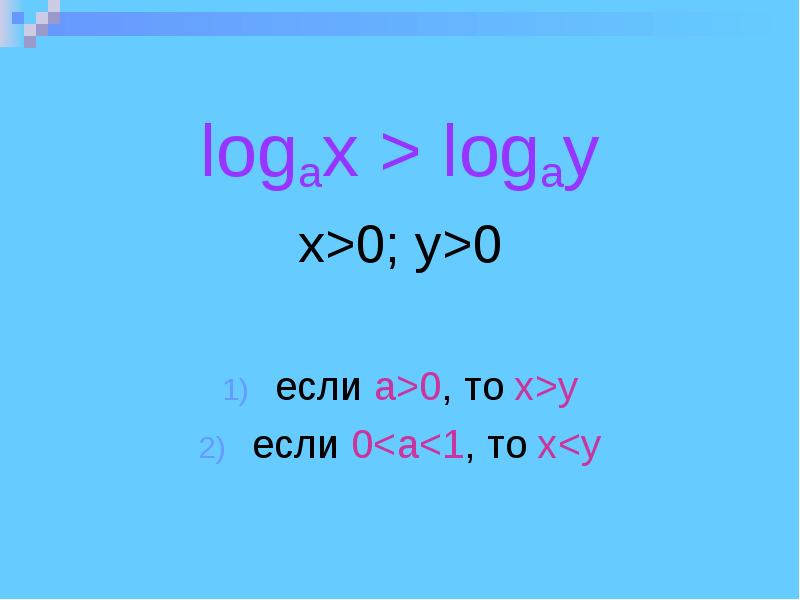



![log2x≤1 ответы:
(0;2]
log3x<2 log2x≤1 ответы:
(0;2]
log3x<2](/documents_2/571ca459b03fc7542f4df6e3011b3314/img6.jpg)


Слайды и текст этой презентации
Презентация на тему Логарифмические неравенства доступна для скачивания ниже:
Похожие презентации





























