Применение производной для исследования функции

«Применение производной для исследования функции»

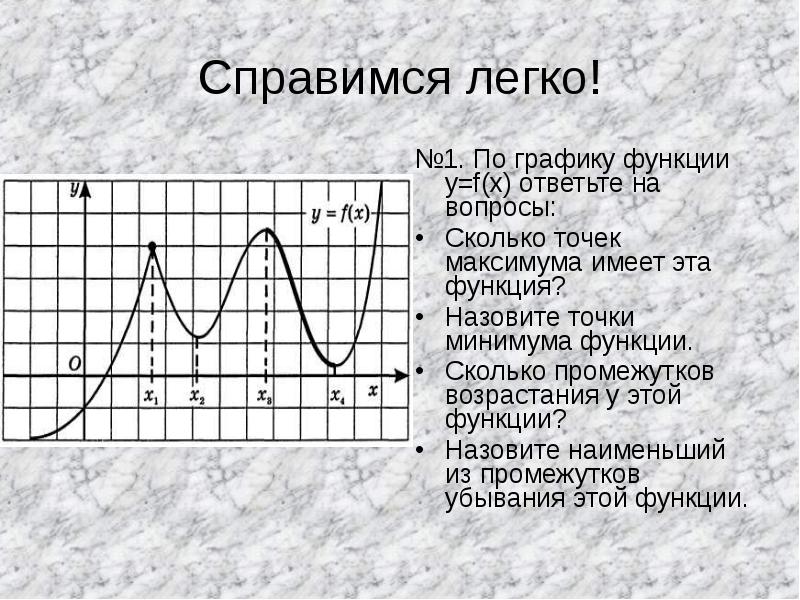
Справимся легко! №1. По графику функции y=f(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько промежутков возрастания у этой функции? Назовите наименьший из промежутков убывания этой функции.

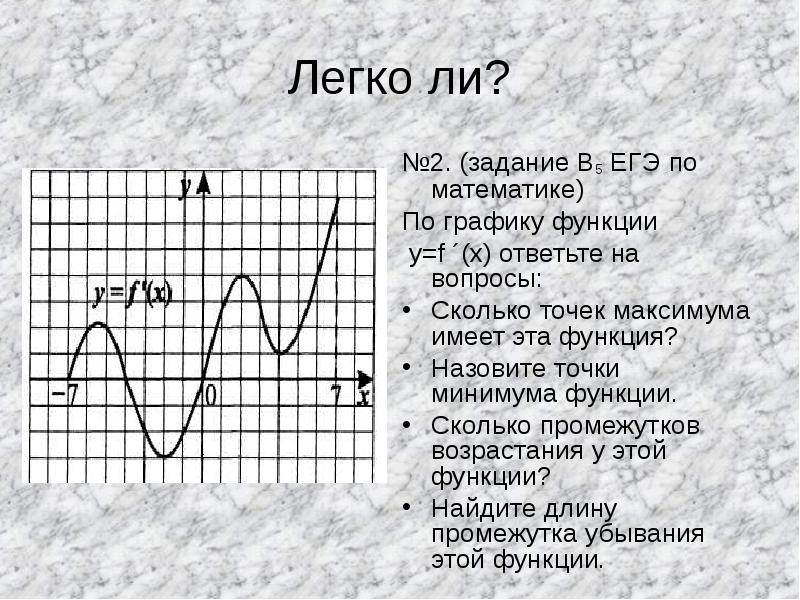
Легко ли? №2. (задание В5 ЕГЭ по математике) По графику функции y=f ´(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько промежутков возрастания у этой функции? Найдите длину промежутка убывания этой функции.

Для нас задача… Составить (создать, разработать) правило (алгоритм), с помощью которого можно исследовать функции на монотонность и экстремумы по её производной.

Теорема 1 Если во всех точках открытого промежутка Х производная f ´(x) больше или равна нулю (причем f ´(x) =0 лишь в отдельных точках), то функция y=f (x) возрастает на промежутке Х.

Теорема 2 Если во всех точках открытого промежутка Х производная f ´(x) меньше или равна нулю (причем f ´(x) =0 лишь в отдельных точках), то функция y=f (x) убывает на промежутке Х.

Теорема 3 Если функция y=f (x) имеет экстремум в точке х0, то в этой точке производная функции либо равна нулю, либо не существует.

№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции.

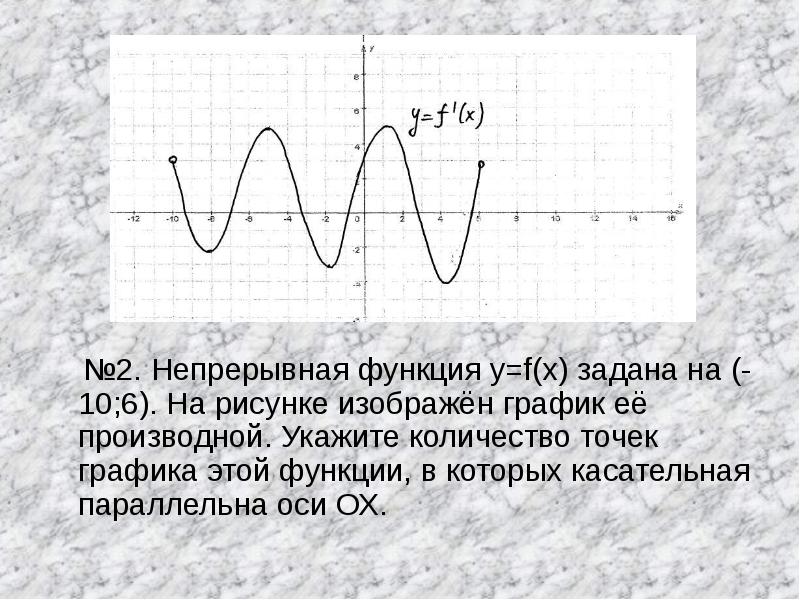
№2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график её производной. Укажите количество точек графика этой функции, в которых касательная параллельна оси ОХ.

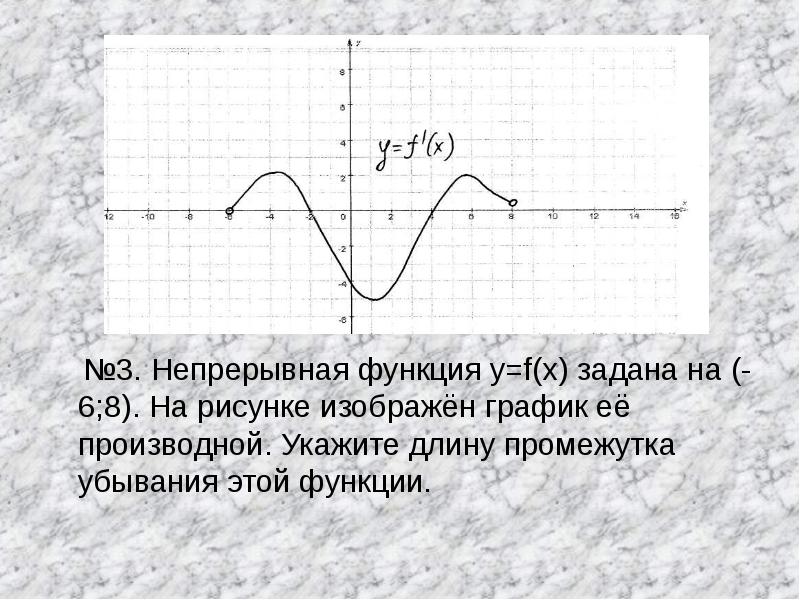
№3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график её производной. Укажите длину промежутка убывания этой функции.

№4. Непрерывная функция y=f(x) задана на (-4;10). На рисунке изображён график её производной. Укажите число точек экстремума этой функции.