Тригонометрические функции и их графики

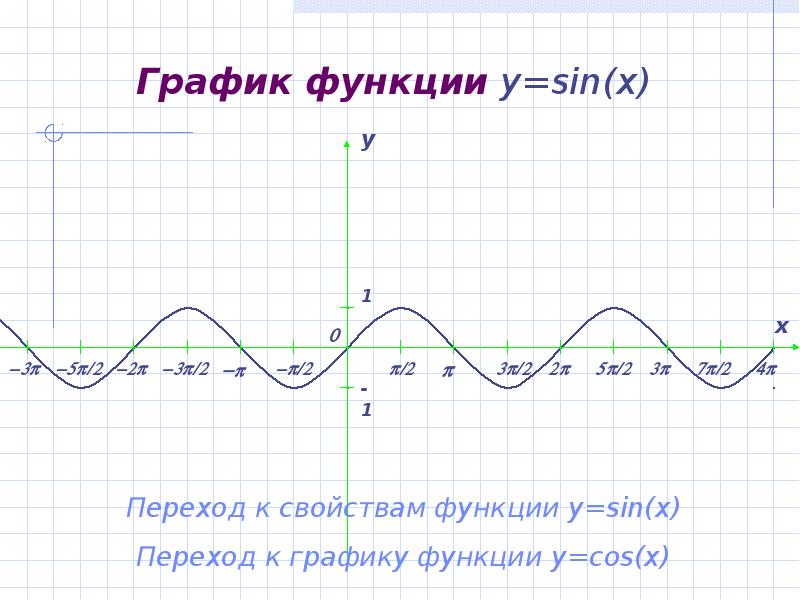
График функции y=sin(x)

Свойства функции y=sin(x) Область определения y=sin(x) – множество R всех действительных чисел. Множество значений y=sin(x) – отрезок [-1;1]. Функция периодическая: sin(x)=sin(x+2n) , n. Функция нечётная: sin(x)=-sin(-x). Функция принимает нулевые значения в точках, кратных  Функция y=sin(x) принимает максимальное значение, равное 1, в точках x=n, n Функция y=sin(x) принимает минимальное значение, равное -1 в точках x=-n , n Между этими точками функция y=sin(x) монотонно убывает или монотонно возрастает. Вернись обратно к графику и найди на нём все указанные свойства функции y=sin(x) !

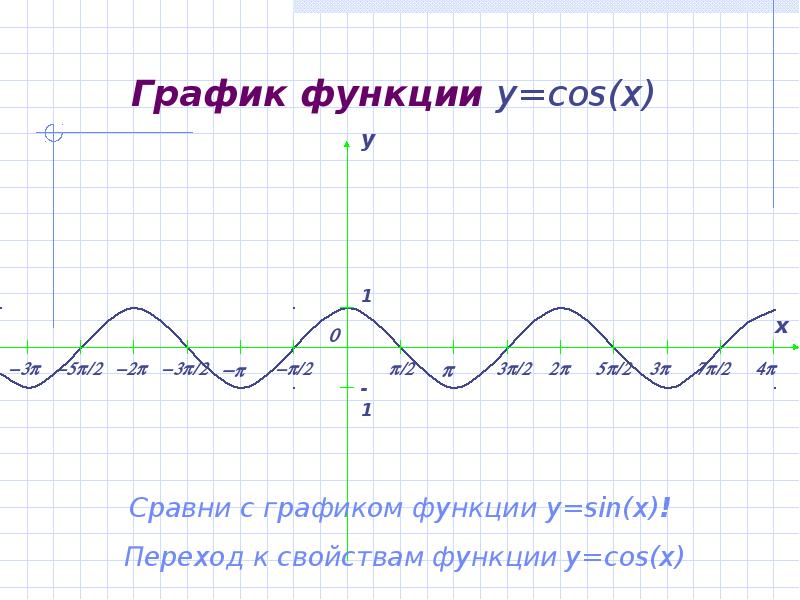
График функции y=cos(x)

Свойства функции y=cos(x) Область определения y=cos(x) – множество R всех действительных чисел. Множество значений y=cos(x) – отрезок [-1;1]. Функция периодическая: cos(x)=cos(x+2n) , n . Функция чётная: cos(x)=cos(-x). Функция y=cos(x) принимает нулевые значения в точках x=n , n  Функция y=cos(x) принимает максимальное значение, равное 1, в точках x=n , n  Функция y=cos(x) принимает минимальное значение, равное -1 в точках x=n+1 )  n   Между этими точками функция y=cos(x) монотонно убывает или монотонно возрастает. Вернись обратно к графику и найди на нём все указанные свойства функции y=cos(x) !

Преобразования графиков функций sin(x) и cos(x) y= -sin(x) y= sin(x-) y= sin(x+/2) y= sin(x-/4) y= sin(x)+2 y= 2sin(x)-1 y= 2sin(x-/4)-1

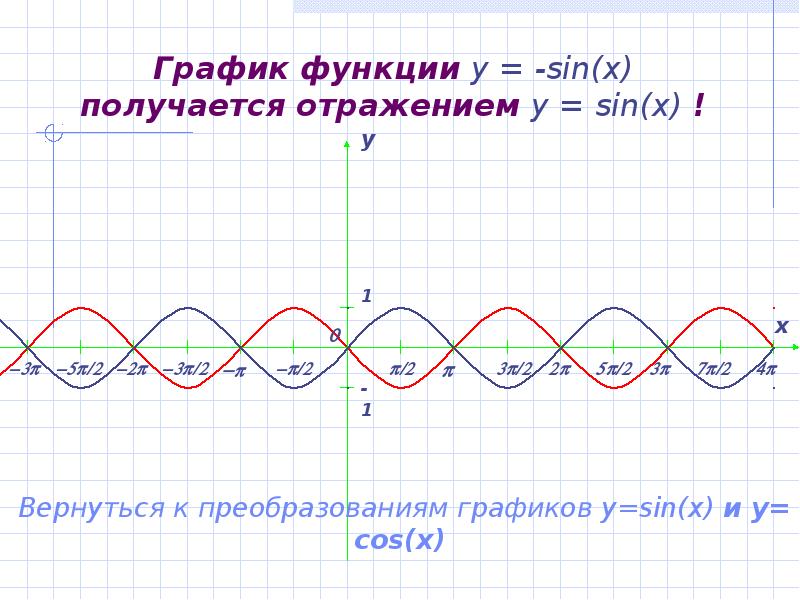
График функции y = -sin(x) получается отражением y = sin(x) !

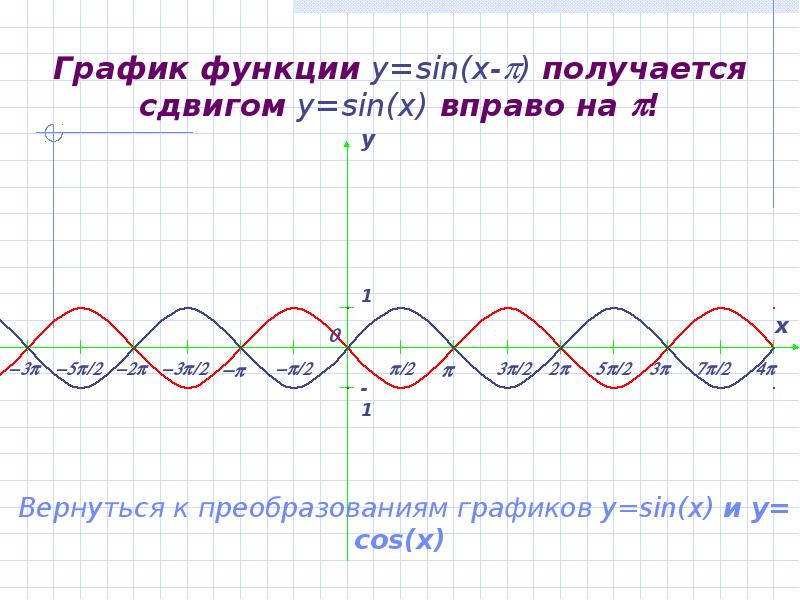
График функции y=sin(x-) получается сдвигом y=sin(x) вправо на !

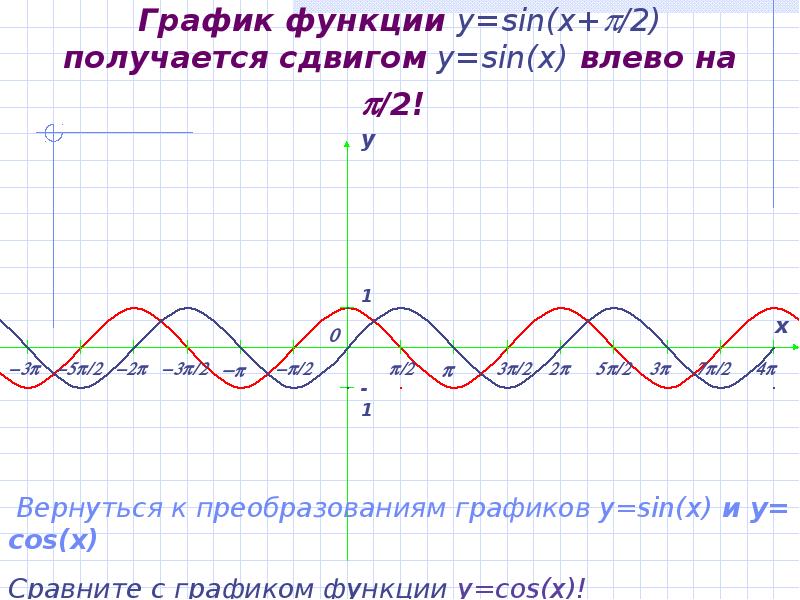
График функции y=sin(x+/2) получается сдвигом y=sin(x) влево на /2!

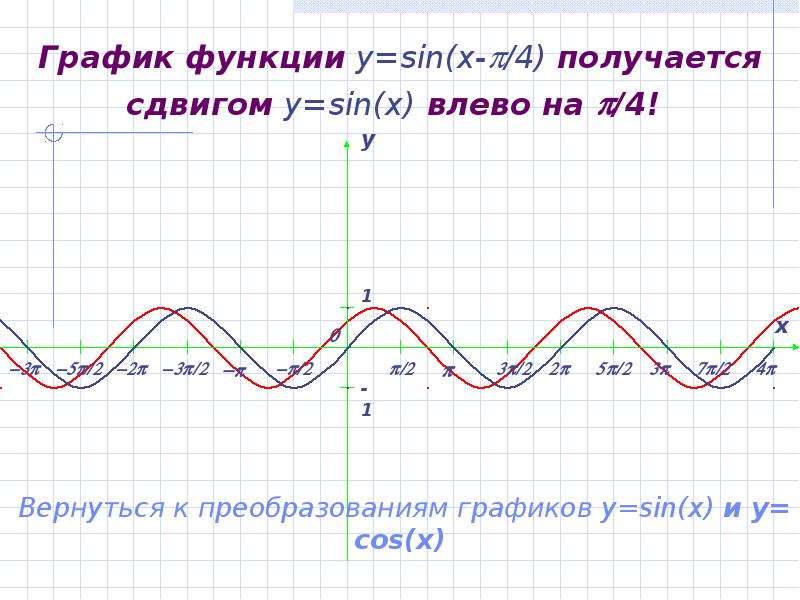
График функции y=sin(x-/4) получается сдвигом y=sin(x) влево на /4!

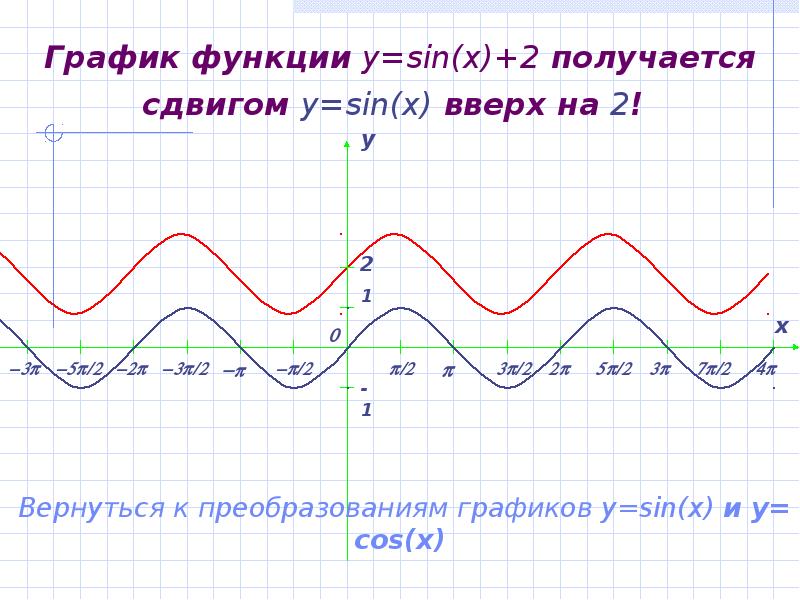
График функции y=sin(x)+2 получается сдвигом y=sin(x) вверх на 2!

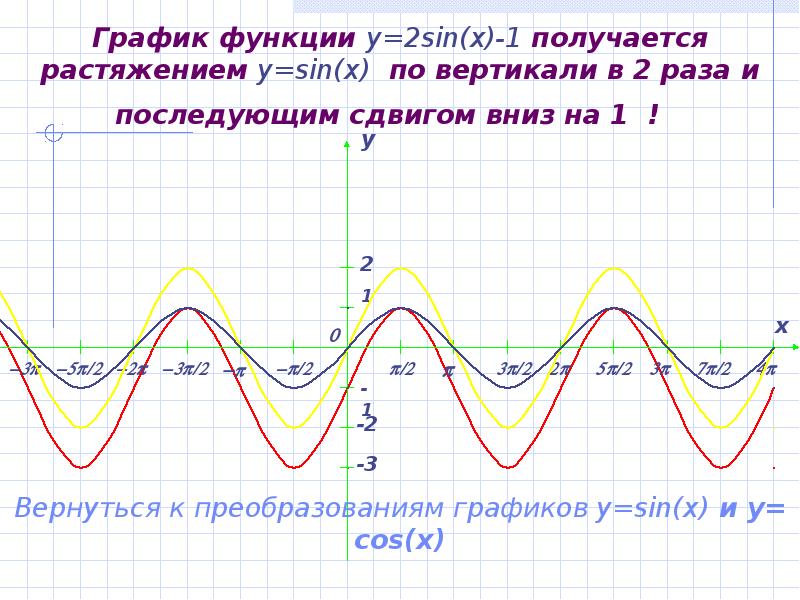
График функции y=2sin(x)-1 получается растяжением y=sin(x) по вертикали в 2 раза и последующим сдвигом вниз на 1 !

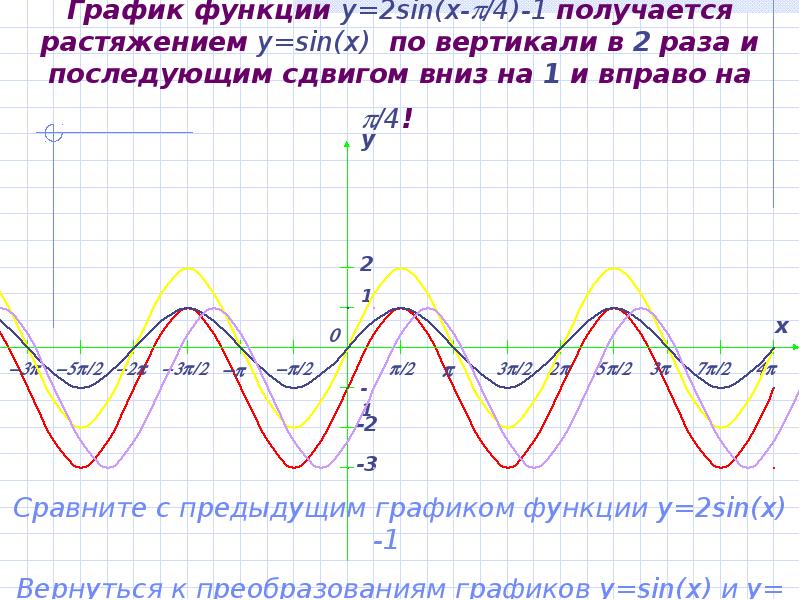
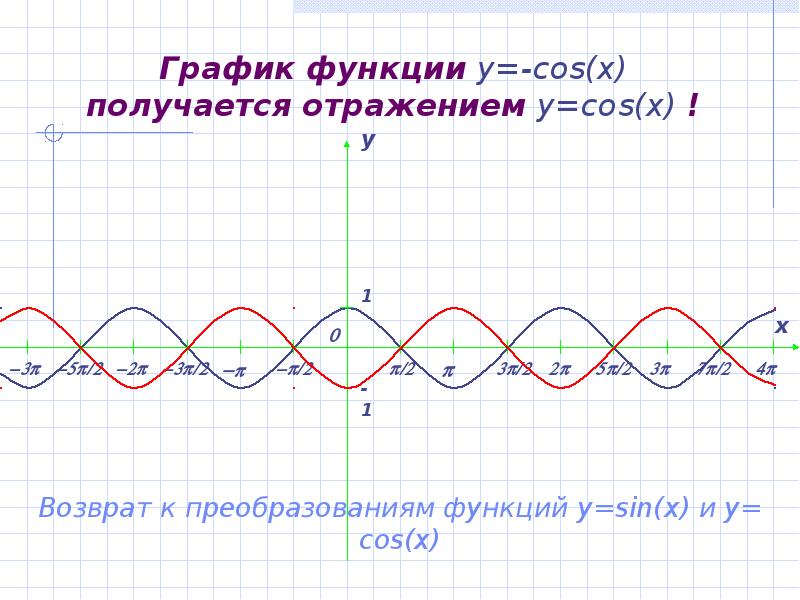
График функции y=2sin(x-/4)-1 получается растяжением y=sin(x) по вертикали в 2 раза и последующим сдвигом вниз на 1 и вправо на /4!

График функции y=-cos(x) получается отражением y=cos(x) !

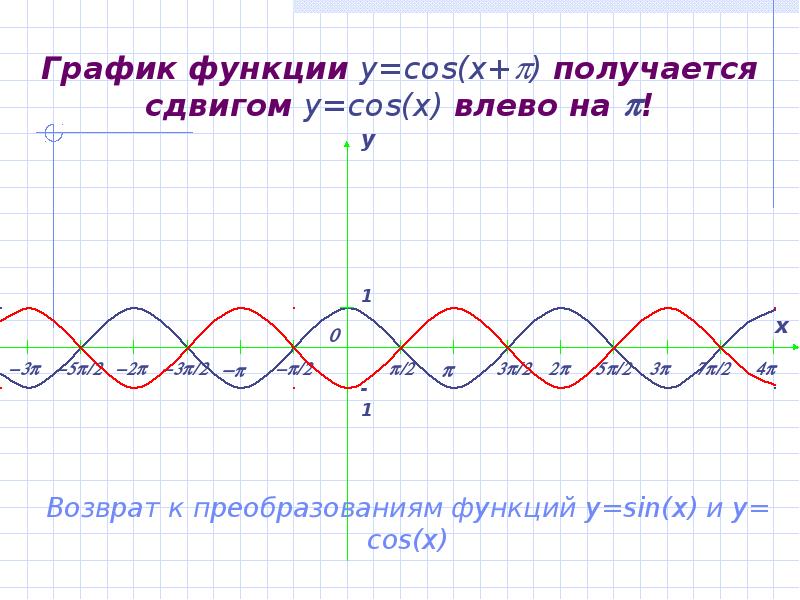
График функции y=cos(x+) получается сдвигом y=cos(x) влево на !

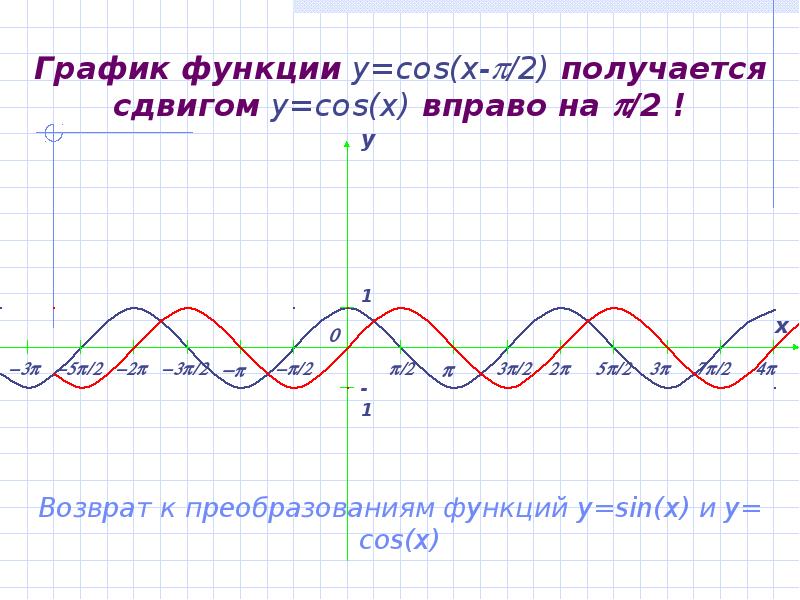
График функции y=cos(x-/2) получается сдвигом y=cos(x) вправо на /2 !

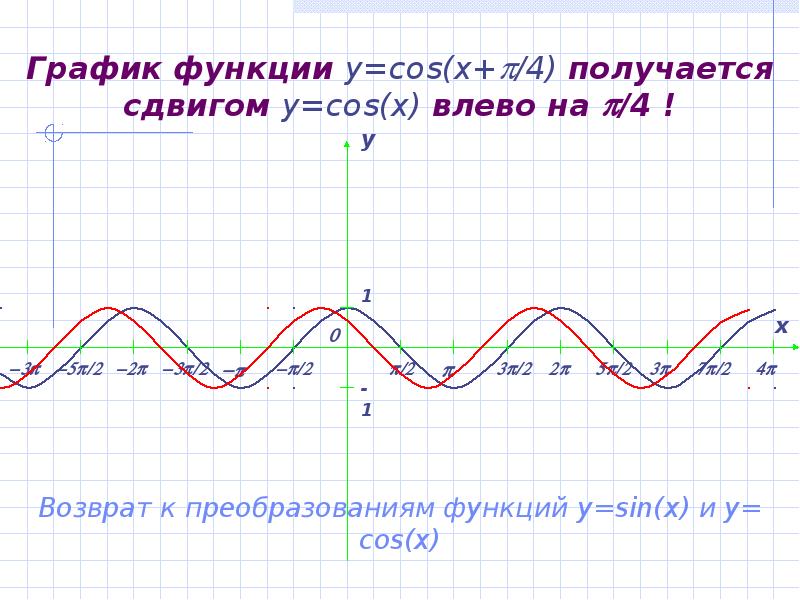
График функции y=cos(x+/4) получается сдвигом y=cos(x) влево на /4 !

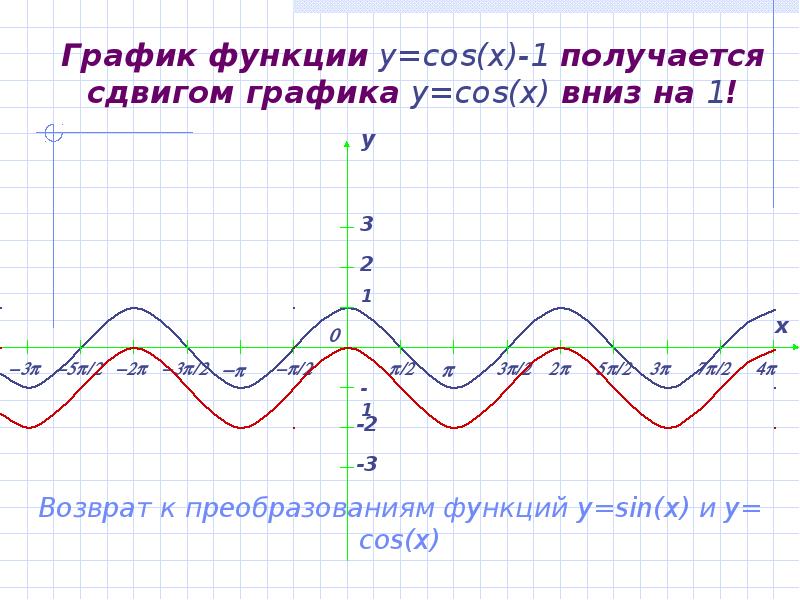
График функции y=cos(x)-1 получается сдвигом графика y=cos(x) вниз на 1!

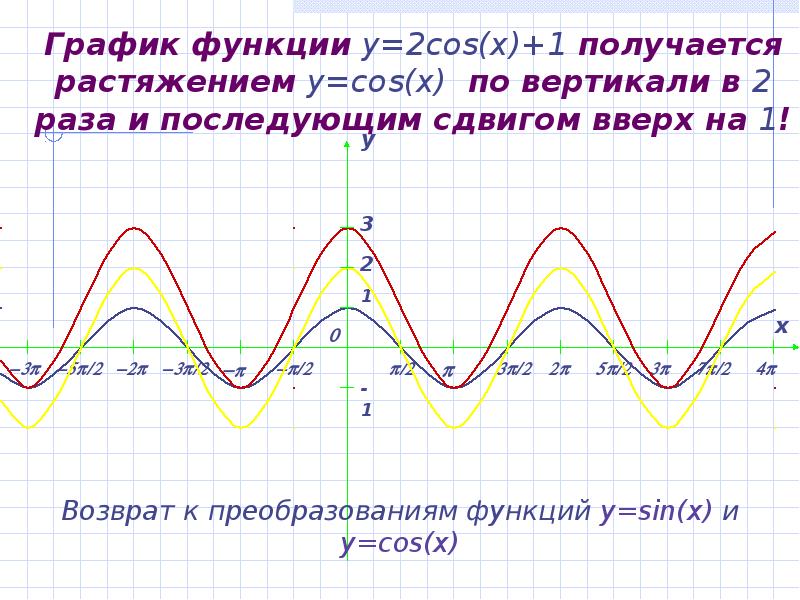
График функции y=2cos(x)+1 получается растяжением y=cos(x) по вертикали в 2 раза и последующим сдвигом вверх на 1!

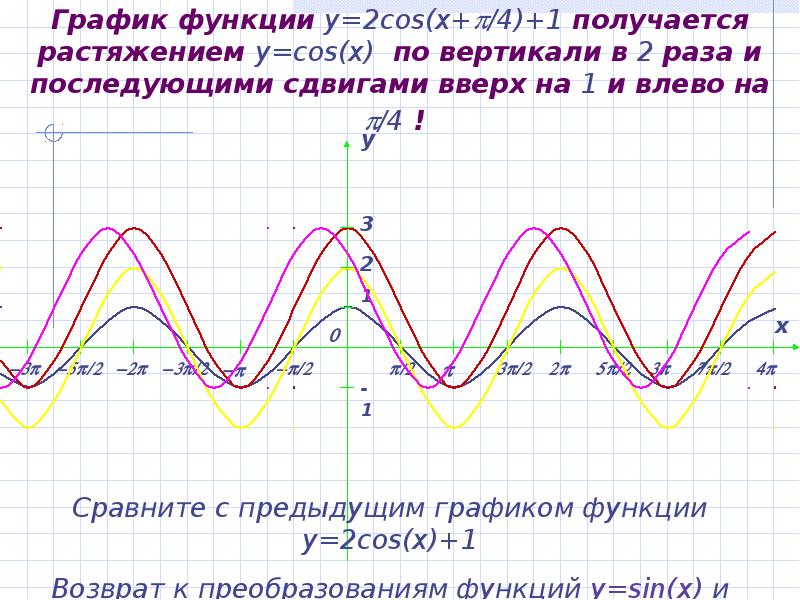
График функции y=2cos(x+/4)+1 получается растяжением y=cos(x) по вертикали в 2 раза и последующими сдвигами вверх на 1 и влево на /4 !